Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числова послідовність. Границя числової послідовності. ТеоремиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Про границі. Нескінченно малі та нескінно великі послідовності
Мета заняття Узагальнити та систематизувати знання студентів з теми. Вивчити теореми про границі послідовностей. Розвивати логічне мислення.
Студенти повинні знати: означення числової послідовності та її границі; теореми про границі послідовностиі; правила знаходження границь ч.п.; поняття збіжної, розбіжної, нескінченно малої та нескеінченно великої послідовностей. Студенти повинні вміти: задавати числову послідовність; знаходити члени послідовності за формулою її загального члена; знаходити границі числової послідовності.
Основні питання теми 1.Числова послідовність; способи завдання; властивості; 2.Границя числової послідовності; геометричне тлумачення границі; 3.Збіжні та розбіжні послідовності; 4.Нескінченно малі та нескінченно великі послідовності; 5.Теореми про границі: необхідна умова існування границі, єдиність гра-ниці, про представлення послідовності сумою її границі та нескінченно малої послідовності, сума двох нескінченно малих послідовностей, до-буток обмеженої та нескінченно малої, границя суми двох послідовнос-тей, границя добутку двох послідовностей, границя частки двох послі-довностей, зв'язок між нескінченно малою та нескінченно великою по-слідовностями; теорема Вейєрштрасса; 6.Число е;
Свої набуті знання ви можете перевірити в наступному тесті 1.Якщо областю визначення функції є множина натуральних чисел, то функція називається... а)натуральною функцією б)похідною послідовністю в)первісною функцією г)числовою послідовністю 2.Якщо для будь-якого числа ε існує такий номер N, що при всіх n > N виконується нерівність |аn – а| < ε, то число а називається... а)обмеженням послідовності б)розбіжністю послідовності в)границею послідовності г)збіжністю послідовності 3.Якщо послідовність не має границю, то вона називається... а)збіжною б)розбіжною в)нескінченно малою г)нескінченно великою 4.Якщо границя послідовності дорівнює "+" або " – " нескінченності, то вона називається... а)збіжною б)розбіжною в)нескінченно малою г)нескінченно великою 5.Якщо для будь-якого члена послідовності виконується нерівність: наступний член менший за попередній, то послідовність називається... а)зростаючою б)спадною в)незростаючою г)неспадною 6.Якщо послідовність аn нескінченно мала, то послідовність 1/аn буде... а)обмеженою б)необмеженою в)нескінченно великою г)нескінченно малою 7.Добуток обмеженої послідовності на нескінченно малу буде послідовністю... а)обмеженою б)необмеженою в)нескінченно великою г)нескінченно малою 8.Якщо послідовність має границю, то вона... а)обмежена б)необмежена в)стала г)неперервна 9.Будь – яка збіжна послідовність... а)має тільки одну границю б)не має границі в)має завжди дві границі г)є розбіжною 10.Границя суми двох нескінченно малих послідовностей є послідовністю... а)обмеженою б)необмеженою в)нескінченно великою г)нескінченно малою
Завдання для самоперевірки 1.Записати перші шість членів числової послідовності а) хn = (2n + 1)/n б)уn = (n + (-1)nn)/n 2.Довести, що наступна послідовність не має границі хn = (n + 1)/n, n = 1,3,5,…. 1/n, n = 2,4,6,… 3.Куди прямують наступні послідовності? а) хn = n! б) yn = - n3 в) zn = n2cosπn. Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001, стор. 149 – 155. Лекція „Послідовність. Границя послідовності і функції” Означення. Якщо задана закономірність, згідно з якою кожному натуральному числу 1, 2, 3, …, відповідає деяке дійсне число, то говорять, що задано послідовність. Послідовність можна розглядати як функцію, областю визначення якої є множина натуральних чисел.
Послідовність визначається формулою, тобто законом, згідно з яким установлюється спосіб відповідності заданих чисел послідовним натуральним числам. Послідовність із загальним членом аn позначається У прикладі: Інший спосіб визначення послідовності полягає в застосуванні рекурсії: n -й член послідовності визначається за допомогою заданих
Приклади послідовностей. 1) 3) Обмежені та монотонні послідовності Означення. Послідовність
виконується для всіх n. Означення. Послідовність
для всіх n.
1) 2) · За означенням відповідно обмеженої та монотонної послідовності маємо: 1)
2) 3)
4)
Означення. Послідовність хn називається обмеженою зверху, якщо існує число m, таке що при всіх n = 1, 2, 3, … виконується нерівність Означення. Послідовність хn називається обмеженою знизу, якщо існує число m, таке що при всіх n = 1, 2, 3, … виконується нерівність Означення. Послідовність хn, не обмежена зверху або знизу, називається необмеженою.
обмежена зверху та знизу:
обмежена зверху, але не обмежена знизу. Означення. Множина довільних точок Х на числовій осі називається обмеженою зверху, якщо існує число т, таке що для всіх Означення. Множина довільних точок Х на числовій осі називається обмеженою знизу, якщо існує число m, таке що для всіх, Множина, для якої існують верхня та нижня межі, називається обмеженою. Найменша серед верхніх меж називається супремумом і позначається Означення. Точною верхньою межею множини Х називається значення 1) для будь-якого 2) для будь-якого
Аналогічно означується точна нижня межа множини Х. Теорема. У будь-якої обмеженої множини існують точні верхня та нижня межі. Збіжні та розбіжні послідовності Означення. Число а називається границею послідовності
Позначення: Графічна ілюстрація
Рис. 1 Означення. Послідовність, яка має границю, називається збіжною, а яка не має границі називається розбіжною.
Властивості збіжних послідовностей Теорема 1. Границя сталої дорівнює цій сталій:
Доведення. Справді,
Теорема 2. Якщо послідовність хn має границю, то ця границя єдина. Доведення. Припустимо супротивне. Нехай
Для визначеності візьмемо, що
А оскільки водночас
Візьмемо Оцінімо
тобто Це неправильна (хибна) нерівність. Дістали суперечність, яка й доводить теорему.¨ Теорема 3. Послідовність хn, яка має границю, є обмеженою. Доведення. Нехай
Позначимо
Тоді для всіх n
тобто послідовність хn обмежена.¨ Теорема 4. Нехай
Доведення. Візьмемо довільне значення e, наприклад Теорема 5. Нехай
Доведення. Припустимо супротивне, тобто
Тоді згідно з теоремою 4 можна стверджувати, що починаючи з деякого номера n виконуватиметься нерівність
А це суперечить умові теореми. Отже, припущення неправильне. ¨ Теорема 6. Якщо
Доведення. Припустимо супротивне. Нехай
Тоді Означення. Перехід від нерівності Теорема 7 (про «охоплену» послідовність або теорема про двох міліціонерів). Нехай виконується нерівність Доведення. Візьмемо довільне
Розглянувши підкреслені нерівності, запишемо:
Остаточно дістанемо
При всіх n виконується нерівність Оскільки Теорема 8. (Больцано–Вейєрштрасса). Будь-яка монотонна обмежена послідовність має границю. Доведення. Розглянемо множину значень послідовності Позначимо Із нерівностей Це означає, що Число е Розглянемо послідовність чисел
Доведемо, що послідовність хn монотонно зростає. За формулою бінома Ньютона маємо:
Замінимо в цьому розкладі n на n + 1. Тоді число доданків збільшиться на одиницю. Далі маємо:
Кожний вираз, що містить n, зростає, тобто Доведемо обмеженість послідовності хn. У формулі (3) значення кожного виразу в дужках менше від одиниці. Отже,
За формулою суми геометричної прогресії маємо:
Звідси
За теоремою Больцано–Вейєрштрасса послідовність Означення. Границя послідовності Позначення:
Число е* — (так зване Неперове число). Для кращого розуміння означення границі послідовності розглянемо приклади: Приклад. Використовуючи означення границі послідовності довести, що Згідно з означенням границі послідовності для довільного Проілюструємо одержаний результат табличкою:
Тоді при Приклад. Використовуючи означення границі функції, довести, що Згідно з означенням границі функції для будь-якого З наведених прикладів зрозуміло, що завдання знаходження границі послідовності і функції з використанням означення досить складне. Формально для знаходження границі треба у вираз функції підставити число, до якого прямує х. Якщо в результаті підстановки одержується число, то воно дорівнює границі функції, але, як правило, за такої підстановки одержують так звану невизначеність вигляду: Приклади. Знаходження границь: 1) 2) 3) 4) 5) 6) 7) Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001, стор. 149 – 155.
Тема 11
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1674; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.28.200 (0.013 с.) |



 , або просто аn.
, або просто аn. .
. попередніх членів послідовності.
попередніх членів послідовності.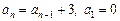 визначає послідовність 0, 3, 6, 9, ….
визначає послідовність 0, 3, 6, 9, …. визначає послідовність 1, 2, 5, 27, 734, ….
визначає послідовність 1, 2, 5, 27, 734, ….
 ; 2)
; 2) 
 ;
;
 ; 4)
; 4) 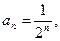
 ;
; називається обмеженою, коли існує таке додатне число М, що нерівність
називається обмеженою, коли існує таке додатне число М, що нерівність
 називається монотонно зростаючою (спадною), якщо
називається монотонно зростаючою (спадною), якщо
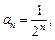
 .
. — обмежена послідовність;
— обмежена послідовність; монотонна спадна послідовність;
монотонна спадна послідовність; — необмежена послідовність;
— необмежена послідовність;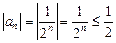 — обмежена послідовність;
— обмежена послідовність; — монотонно спадна послідовність;
— монотонно спадна послідовність;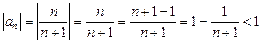 — послідовність обмежена;
— послідовність обмежена;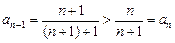 , оскільки
, оскільки — послідовність монотонно зростаюча. ·
— послідовність монотонно зростаюча. · .
. .
. , для якої
, для якої
 .
. , тобто
, тобто
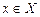 виконується нерівність
виконується нерівність  . Число т називається верхньою межею множини.
. Число т називається верхньою межею множини. виконується нерівність
виконується нерівність  . Число m називається нижньою межею множини.
. Число m називається нижньою межею множини. . Найбільша серед нижніх меж називається інфімумом і позначається
. Найбільша серед нижніх меж називається інфімумом і позначається  .
. , таке що:
, таке що: ;
; знайдеться значення
знайдеться значення 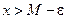 .
. , якщо для кожного як завгодно малого додатного числа
, якщо для кожного як завгодно малого додатного числа  існує таке число
існує таке число  , що
, що для всіх
для всіх  .
. .
.
 — збіжна, оскільки існує
— збіжна, оскільки існує  (за означенням
(за означенням  для будь-якого
для будь-якого  ).
). Зауваження. Послідовність, границя якої дорівнює 0, називається нульовою послідовністю.
Зауваження. Послідовність, границя якої дорівнює 0, називається нульовою послідовністю. розбіжна, оскільки не має границі. Вона почергово набуває значення + 1 і – 1.
розбіжна, оскільки не має границі. Вона почергово набуває значення + 1 і – 1. .
. для всіх n, тому
для всіх n, тому . ¨
. ¨ і
і  , причому
, причому  .
.
 і
і  . Оскільки
. Оскільки  виконується нерівність
виконується нерівність . (1)
. (1) , то знайдеться число N 2, таке що при
, то знайдеться число N 2, таке що при 
 . (2)
. (2) . При
. При  одночасно виконуються обидві нерівності (1), (2).
одночасно виконуються обидві нерівності (1), (2). ,
, .
. , наприклад e = 1. Тоді знайдеться число N, таке що при всіх
, наприклад e = 1. Тоді знайдеться число N, таке що при всіх  . Звідси випливає:
. Звідси випливає: .
. .
. ,
, . Тоді знайдеться число N, таке що при будь-якому
. Тоді знайдеться число N, таке що при будь-якому  справджуватиметься нерівність
справджуватиметься нерівність .
.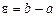 . Тоді знайдеться число N, таке що при
. Тоді знайдеться число N, таке що при  . Тоді
. Тоді  або
або 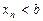 .
. , то
, то .
.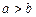 .
.
 .
. і
і  ,
,  .
.
 . Тоді згідно з теоремами 4 і 5, починаючи з деякого номера виконуватимуться нерівності
. Тоді згідно з теоремами 4 і 5, починаючи з деякого номера виконуватимуться нерівності .
.
 , що суперечить умові. Отже, припущення неправильне. ¨
, що суперечить умові. Отже, припущення неправильне. ¨ . Якщо послідовності хn і уn збіжні, причому
. Якщо послідовності хn і уn збіжні, причому 
 , то послідовність un також буде збіжною і
, то послідовність un також буде збіжною і  .
. виконується нерівність
виконується нерівність  . Візьмемо
. Візьмемо  . Тоді при
. Тоді при  або
або 
 .
. , або
, або  , тобто для довільного
, тобто для довільного  можна знайти N, таке що при
можна знайти N, таке що при 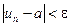 , що означає, що
, що означає, що  . ¨
. ¨ .
. .
. то
то  .·
.· . Ця множина обмежена, тому вона має точну верхню і нижню межі. Для визначеності вважатимемо, що послідовність хn монотонно зростає.
. Ця множина обмежена, тому вона має точну верхню і нижню межі. Для визначеності вважатимемо, що послідовність хn монотонно зростає. і доведемо, що
і доведемо, що 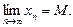 При всіх n за умовою теореми виконується нерівність
При всіх n за умовою теореми виконується нерівність  Візьмемо довільне
Візьмемо довільне  За означенням точної верхньої межі можна знайти значення
За означенням точної верхньої межі можна знайти значення  , таке що
, таке що  . Оскільки послідовність монотонно зростає, то при
. Оскільки послідовність монотонно зростає, то при  маємо
маємо 
 випливає:
випливає:  і
і 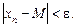
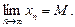 ¨
¨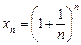 . Обчислимо кілька перших значень членів послідовності:
. Обчислимо кілька перших значень членів послідовності:

 (3)
(3)
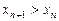 .
.


 має границю.
має границю. називається числом е.
називається числом е.
 .
. треба знайти такий номер елемента послідовності N, що для всіх
треба знайти такий номер елемента послідовності N, що для всіх  виконувалася б нерівність
виконувалася б нерівність  . Нехай вибрано
. Нехай вибрано 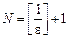 , тоді
, тоді  і для будь-якого
і для будь-якого 
 .
. , починаючи з
, починаючи з  , відповідні п можна брати з послідовності
, відповідні п можна брати з послідовності  Для них
Для них  . Якщо
. Якщо  , а
, а  , то тепер п можна брати з послідовності
, то тепер п можна брати з послідовності  і знову нерівність
і знову нерівність  виконується. Отже, для будь-якого навіть нескінченно малого значення e можна знайти N, що для всіх
виконується. Отже, для будь-якого навіть нескінченно малого значення e можна знайти N, що для всіх  виконується. Це й означає, що
виконується. Це й означає, що  .
.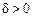 , що для тих х, для яких виконується не-
, що для тих х, для яких виконується не- , виконується й нерівність
, виконується й нерівність  . Нехай вибрано деяке
. Нехай вибрано деяке  . Тоді
. Тоді 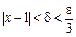 .
.  . Тобто
. Тобто  і т. п. Для розкриття невизначеності дещо перетворюють вираз функції, що стоїть під знаком границі, і використовують відповідні теореми теорії границь або одну з особливих границь.
і т. п. Для розкриття невизначеності дещо перетворюють вираз функції, що стоїть під знаком границі, і використовують відповідні теореми теорії границь або одну з особливих границь. .
. .
. .
.
 .
.
 .
.
 .
.