Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Можливі варіанти розриву функцій в точціСодержание книги
Поиск на нашем сайте
Рис. 4
Рис. 5
Рис. 6
Методика дослідження 1. Знаходимо точку х 0 — «підозрілу» на розрив. Це може бути точка, в якій функція невизначена або змінює закон визначеності. 2. Визначаємо інтервали неперервності функції. 3. Обчислюємо
4. Робимо висновок згідно з теоремами (якщо такі границі існують), або використовуючи означення точок розриву.
Рис. 7 1. Точка х 0 = 1 є «підозрілою» на розрив, оскільки в ній функція змінює закон визначеності (на проміжку (– ¥; 1) маємо у = х, на проміжку (1, +¥) — іншу залежність: у = х + 1). 2. Функція неперервна на проміжках (– ¥; 1) і (1; + ¥). 3. Знаходимо
4.
· 1. Точка х 0 = 0 є «підозрілою» на розрив, оскільки в ній функція змінює закон визначеності. 2. (– ¥; 0) 3. Знаходимо
1 = 1 =1 — функція неперервна в точці х 0 = 0 за означенням неперервної функції. Отже, інтервалом неперервності функції Наслідки з формул для визначних границь 1. 4. Досліджуючи функції на неперервність, слід пам’ятати, що елементарна функція може мати розрив тільки в окремих точках, в яких вона невизначена. Неелементарна функція може мати розриви у точках, де вона невизначена, а також у тих точках, при переході через які змінюється її аналітичний вираз. Дослідження функції на неперервність полягає в знаходженні точок, в яких можливий розрив, з подальшою перевіркою умов неперервності функції. Перевірка умов переважно зводиться до знаходження односторонніх границь функції, коли х прямує до можливої точки розриву зліва або справа, і до подальшого порівняння значень цих границь, якщо вони існують. Приклад. Дослідити на неперервність функції: 1) 2) 3) схематично побудувати їх графіки.
Приклад. Дослідження на неперервність функції:
При якому значенні а функція буде неперервною? Побудувати схематично графік при різних значеннях а. Задана функція не є елементарною, хоча на кожному з проміжків вона задається елементарними функціями. Можлива точка розриву є точка переходу від одного аналітичного виразу до іншого
Література: В.П.Дубовик, І.І.Юрик„Вища математика”, К.,”АСК”,2001, стор. 183 – 189.
Розділ”Диференціальне числення функції однієї змінної” Тема 12 Задачі, що приводять до поняття похідної. Означення похідної. Фізичний та геометричний зміст похідної. Таблиця похідних. Похідна складеної та оберненої функцій
Мета заняття Узагальнити та систематизувати знання про похідну, виховувати вміння самостійно відпрацьовувати тему, розвивати логічне мислення.
Студенти повинні знати: означення похідної функції в точці, фізичний та геометричний зміст похідноїї; таблицю похідних основних елементарних функцій; основні формули диференціювання. Студенти повинні вміти: знаходити похідні за означенням та за таблицею; користуватися правилами диференціювання.
Основні питання теми 1.Задачі, що приводять до поняття похідної (задача про миттєву швидкість руху точки, миттєву силу струму і т.п.); фізичний зміст похідної функції в точці; 2.Означення похідної функції в точці; 3.Геометричний зміст похідної функції в точці; 4.Таблиця похідних; 5.Похідна складеної функції; 6.Похідна оберненої функції 7.Приклади.
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.49.90 (0.006 с.) |


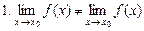 (рис. 4)
(рис. 4)
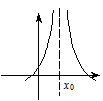
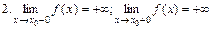 (рис. 5).
(рис. 5).
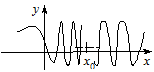
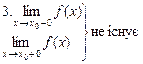 (рис. 6)
(рис. 6)
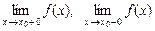 і при цьому:
і при цьому:
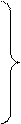
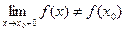 або
2.
або
2. 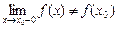 або
3.
або
3. 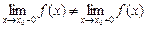 або
або
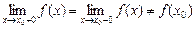 — усувний розрив 1-го роду
— усувний розрив 1-го роду
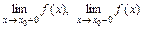 не існує або нескінченна.
не існує або нескінченна.
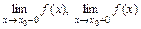 .
. Дослідити на неперервність функцію
Дослідити на неперервність функцію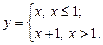

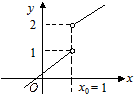
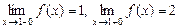 .
.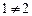 , тому за означенням функція
, тому за означенням функція 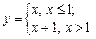 має в точці х = 1 неусувний розрив 1-го роду.
має в точці х = 1 неусувний розрив 1-го роду.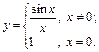
 (0; + ¥) — множина, де функція неперервна.
(0; + ¥) — множина, де функція неперервна.
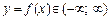 .
.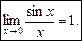 2.
2.  3.
3.  .
.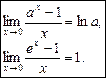 . 5.
. 5. 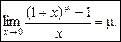
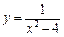 ;
;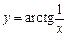 ;
;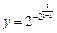 ,
,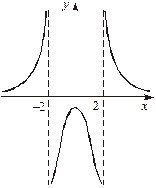
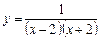 . Можливі точки розриву (функція невизначена в цих точках):
. Можливі точки розриву (функція невизначена в цих точках): 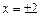 . Оскільки функція парна, то її поведінка в околі цих точок однакова. Дослідимо точку
. Оскільки функція парна, то її поведінка в околі цих точок однакова. Дослідимо точку 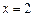 . Функція визначена в околі цієї точки, знайдемо
. Функція визначена в околі цієї точки, знайдемо 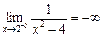 і
і 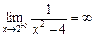 . Отже, односторонні границі не існують, тому в точці
. Отже, односторонні границі не існують, тому в точці 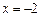 функція має розрив другого роду.
функція має розрив другого роду.
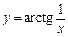 . Точка можливого розриву —
. Точка можливого розриву — 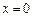 . Знайдемо
. Знайдемо 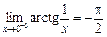 ,
, 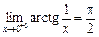 . Обидві односторонні границі функції існують, але нерівні між собою. В точці
. Обидві односторонні границі функції існують, але нерівні між собою. В точці 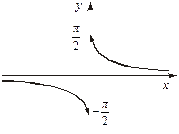
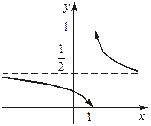
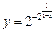 . Точка можливого розри- ву —
. Точка можливого розри- ву — 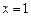 . Знайдемо
. Знайдемо 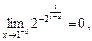
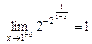 . Односторонні грани- ці існують, але нерівні між собою. В точці
. Односторонні грани- ці існують, але нерівні між собою. В точці 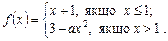
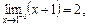
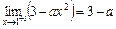 . Згідно з означенням, якщо границі рівні між собою і рівні значенню функції в точці
. Згідно з означенням, якщо границі рівні між собою і рівні значенню функції в точці 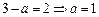 . При
. При 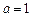 функція неперервна в точці
функція неперервна в точці 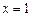 , а при інших значеннях а в цій точці розрив першого роду.
, а при інших значеннях а в цій точці розрив першого роду.