
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференціювання неявної функціїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
І. Функція двох змінних. Функція
Розв’язавши рівняння (11) відносно Це так звана формула диференціювання неявної функції. Нею подаються відносні швидкості зміни значень х щодо значень у, чим забезпечується незмінність f (x, y). Геометрично це означає, що точка (x, y) рухається вздовж кривої, рівняння якої є и = f (x, y), а (12) визначає для будь-якого моменту напрям її руху.
●Нехай
З рівняння (12) знаходимо:
●Нехай
знаходимо частинні похідні цієї функції за х і за у:
Підставляючи в (18), маємо:
За умовою х = 3, у = 1,
1. ● 2. ● 3. ● 4. ● 5. ●
Функція трьох змінних. Нехай Р (х, у, z) — точка на поверхні, заданій рівнянням:
і нехай РС і АР — перерізи, що утворюються площинами, проведеними через точку Р паралельно площинам Y 0 Z і X 0 Z (рис. 3). Для точок кривої АР змінна у лишається сталою. Отже, згідно з (13) z є неявною функцією лише х, а на підставі (16) виконується рівність:
Геометрична інтерпретація. Формула (14) визначає тангенс кута нахилу кривої АР у точці Р до осі0 х.
Рис. 3 У лівій її частині замість Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 Гл.6, стор. 294- 318.
Тема 18 Локальні екстремуми функції багатьох змінних.
Мета заняття Засвоєння поняття локальних екстремумів функції двох змінних. Розвивати логічне мислення, уважність
Студенти повинні знати: формули похідної складеної функції, повної похідної, локальних екстремумів. Студенти повинні вміти: обчислювати похідну складеної функції,повну похідну, локальні екстремуми функцій багатьох змінних. Основні питання теми 1.Поняття точки локального максимуму; 2.Поняття точки локального мінімуму; 3.Необхідні умови екстремуму; 4.Критичні точки функції; 5.Достатні умови екстремуму; 6.Другі достатні умови екстремуму; 7.Правила дослідження диференційованих функцій на екстремум; 8.Приклади.
Завдання для самоперевірки 1.Відкритий прямокутний басейн повинен мати об'єм V. Знайти розміри басейну, за яких на його облицювання піде найменша кількість матеріалу. 2.Знайти екстремуми функції z = х4 + у4 – 2х2 + 4ху – 2у2. 3.Закінчте вирази: - Точка - Точка - Необхідні умови екстремуму функції багатьох змінних полягають у тому, що … - Формула Тейлора для функції двох змінних має вигляд: … - Критерій Сільвестра додатної визначеності квадратичної форми має вигляд: … - Достатні умови існування екстремуму функції багатьох змінних формулюються так: … - Поняття умовного екстремуму функції багатьох змінних полягає у тому, що … - Задача про умовний екстремум функції багатьох змінних 4. Вкажіть правильний розв’язок задачі. Для знаходження найбільшого значення функції а) в стаціонарних точках області б) у точках умовного екстремуму функції в) у стаціонарних точках і точках умовного екстремуму функції г) у стаціонарних точках і точках на межі області Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 Гл.6, стор. 320 – 324.
Для більш глибокого вивчення теми рекомендовано обрати одну із запропонованих тем для написання реферату. Теми рефератів: 1.Застосування частинних похідних. 2.Зображення та застосування функцій багатьох змінних.
Розділ”Інтегральне числення функції однієї змінної” Тема 19 Поняття первісної функції та невизначеного інтегралу. Таблиця основних інтегралів
Мета заняття Узагальнити та систематизувати знання з теми. Розвивати уважність, вміння самостійно визначати головну думку, логічне мислення.
Студенти повинні знати: поняття первісної функції та невизначеного інтегралу, властивості невизначеного інтегралу;основні табличні інтеграли. Студенти повинні вміти: знаходити первісні функції та невизначені інтеграли; використовувати властивості для знаходження первісних та інтегралів.
Основні питання теми 1.Поняття первісної; властивості первісної; 2.Невизначений інтеграл; позначення, властивості; 3.Застосування інваріантності форми першого диференціалу при інтегруванні; 4.Таблиця основних інтегралів; 5.Приклади.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.193.166 (0.006 с.) |

 визначає одну зі змінних х або у як неявну функцію іншої змінної. Поданий вираз — це деяке рівняння, що містить х та у і всі члени якого перенесені в ліву частину. Нехай
визначає одну зі змінних х або у як неявну функцію іншої змінної. Поданий вираз — це деяке рівняння, що містить х та у і всі члени якого перенесені в ліву частину. Нехай 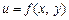 . Тоді
. Тоді  . Проте оскільки
. Проте оскільки  і
і  Звідси
Звідси (11)
(11) (вважаючи, що
(вважаючи, що  і
і  існують), знайдемо залежність
існують), знайдемо залежність  (12)
(12) Для функції
Для функції  знайти
знайти 
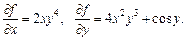
 .
.

 , або
, або  .
. , звідки
, звідки  (дм/с).
(дм/с).
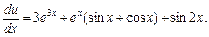








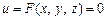 , (13)
, (13) (14)
(14)
 записано
записано  , оскільки згідно з (13) змінна z була спочатку неявною функцією х і у (формулу (14) виведено за припущення, що величина у лишається сталою).
, оскільки згідно з (13) змінна z була спочатку неявною функцією х і у (формулу (14) виведено за припущення, що величина у лишається сталою).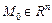 називається точкою максимуму (мінімуму) функції
називається точкою максимуму (мінімуму) функції  , якщо …
, якщо … зводиться до задачі про звичайний екстремум функції …
зводиться до задачі про звичайний екстремум функції …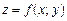 у замкненій області
у замкненій області  з рівнянням межі
з рівнянням межі  потрібно вибрати найбільше значення із обчислених у таких точках:
потрібно вибрати найбільше значення із обчислених у таких точках:


