
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 4. Функції багатьох зміннихСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
74. Множини точок на площині та в n -вимірному просторі. Поняття області. 75. Поняття функції багатьох змінних. Способи задання функції. Виробничі функції. Функція Кобба-Дугласа. 76. Графічне зображення функції та лінії рівня. Область визначення функції. 77. Границя та неперервність функції. Властивості неперервних функцій. 78. Частинні похідні та частинні диференціали функції багатьох змінних. 79. Повний диференціал функції багатьох змінних. 80. Похідна за напрямом функції багатьох змінних. 81. Градієнт функції багатьох змінних. 82. Частинні похідні та диференціали вищих порядків. 83. Екстремум функції багатьох змінних. Необхідні та достатні умови. 84. Поняття про емпіричні формули. Метод найменших квадратів. 85. Умовний екстремум. Метод множників Лагранжа. 86. Оптимізаційні задачі на основі виробничих функцій. 87. Оптимальний розподіл ресурсів.
ІІ СЕМЕСТР Розділ 5. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ 88. Первісна функція. Теорема про множину первісних. 89. Невизначений інтеграл та його властивості. 90. Таблиця невизначених інтегралів. 91. Метод заміни змінної та інтегрування частинами у визначеному інтегралі. 92. Інтегрування виразів, що містять квадратний тричлен. 93. Інтегрування найпростіших раціональних дробів. 94. Інтегрування раціональних дробів. 95. Інтегрування тригонометричних виразів. 96. Інтегрування найпростіших ірраціональних виразів. 97. Задачі що приводять до поняття визначеного інтеграла. 98. Визначений інтеграл та його властивості. 99. Теорема про середнє. 100. Теорема про похідну від інтеграла із змінною верхньою межею. 101. Теорема Ньютона-Лейбніца. 102. Метод заміни змінної та інтегрування частинами у визначеному інтегралі. 103. Наближене обчислення визначеного інтеграла за формулами прямокутників, трапеції та Сімпсона. 104. Геометричне та економічне застосування визначеного інтеграла. 105. Невласні інтеграли. Інтеграл Ейлера-Пуассона. 106. Теореми про порівняння невласних інтегралів. 107. Поняття про подвійний інтеграл. Зведення подвійного інтеграла до повторного. Розділ 6. ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ 108.Основні поняття про диференціальні рівняння та їхні розв’язки. 109. Задача Коші. Теорема існування та єдиності розв’язків. 110. Диференціальні рівняння з відокремленими та відокремлюваними змінними. 111. Лінійні диференціальні рівняння першого порядку. 112. Однорідні диференціальні рівняння першого порядку. 113. Економічні задачі, що приводять до диференціальних рівнянь. Задача адаптації цін по Вальрасу. 114. ЛНДР 2-го порядку з сталими коефіцієнтами. 115. Різницеві рівняння.
Розділ 7. РЯДИ 116. Означення числового ряду та його збіжність. Властивості числових рядів. 117. Необхідна умова збіжності ряду. 118. Достатні умови збіжності рядів з додатніми членами. 119. Знакозмінні ряди. Абсолютна та умовна збіжність знакозмінного ряду. 120. Знакопочережні ряди. Ознака Лейбніца. 121. Степеневі ряди. Теорема Абеля. 122. Радіус, інтервал та область збіжності степеневого ряду. 123. Ряди Тейлора та Маклорена. 124. Розвинення функцій
2. Приклади типових завдань, що виносяться на іспит
1. Обчислити визначник: 1) 2. Розв’язати систему рівнянь за формулами Крамера:
3. Виконати дії: 1)
4. Для матриці А знайти обернену та перевірити результат: 1) 5. Розв”язати систему рівнянь за допомогою оберненої матриці:
6. Розв’язати матричні рівняння 1) 2) 7. Обчислити ранг матриці
8. Дослідити систему рівнянь на сумісність
9. Розв’язати систему рівнянь методом Гаусса – Жордана
10. Довести, що вектори
11. Встановити кількість лінійно незалежних векторів для даної системи векторів
12. Знайти власні числа та власні вектори матриці: 1) 13. Встановити визначеність квадратичної форми:
14. Задана матриця А прямих матеріальних витрат та матриця В кін-цевої продукції
Знайти необхідний обсяг валового випуску (модель Леонтьєва):
15. Паралелограм побудовано на векторах Знайти: 1.Довжину діагоналей паралелограма; 2. Кут між діагоналями; 3. Площу паралелограма; 4. Проекцію 16. Дано трикутник АВС: А (3,2), В (-1,0), С (2,-3). Знайти рівняння: 1. сторони АВ; 2. медіани АЕ; 3. бісектриси СР; 4. висоти ВК; 5. середньої лінії МН що паралельна ВС. Обчислити довжини: 1. сторони АВ; 2. медіани АЕ; 3. бісектриси СР; 4. висоти ВК. Обчислити: 1. Площу трикутника АВС; 2. Кут між медіаною АЕ та бісектрисою СР. 17. Дано ОАВС – піраміда. О (5,-9,-1), А (5,1,2), В (-4,-3,6), С (-9,6,7). Знайти рівняння: 1. грані ОАВ; 2. ребра АО; 3. висоти ОК; 4. площини, що проходить через ребро АО перпендікулярно до основи. Обчислити: 1. площу основи АВС; 2. об’єм піраміди; 3. довжину висоти; 4. кут між ребрами АО та ОВ; 5. віддаль від ребра АО до сторони основи ВС. 18. Задано рівняння кола Знайти: 1. координати центра та довжину радіуса; 2. найкоротшу віддаль від точки М (3,9) до кола; 3. рівняння дотичної із точки К (-5,8) до кола. 19. Знайти ексцентриситет та координати фокусів: 1. еліпса 2. гіперболи 20. Знайти кут між асимптотами гіперболи 21. Знайти область визначення функції
22. Обчислити границі:
23. Встановити характер точок розриву функцій
24. Знайти похідну функції:
25. Знайти диференціал функції:
26. Знайти похідну другого порядку
27. Знайти екстремуми та інтервали монотонності функції:
28. Знайти точки перегину та інтервали напряму опуклості функції:
29. Знайти асимптоти графіка функції
30. Знайти найбільше та найменше значення функції на проміжку [-1;2]. 31. Знайти аналітично та дати геометричну інтерпретацію області визначення функції
32. Знайти повний диференціал функції
33. Знайти частинні похідні функції
34. Знайти частинні похідні другого порядку функції
35. Знайти кут між градієнтами функції В точках (-1;3) і (3;-3). 36. Знайти похідну функції
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |

 у ряд Маклорена.
у ряд Маклорена.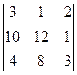 , 2)
, 2)  .
. .
.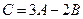 , 2)
, 2)  , якщо
, якщо .
. , 2)
, 2)  .
.
 ,
,  ,
,  , якщо:
, якщо:

 .
. .
. .
. утворюють базис та розкласти вектор
утворюють базис та розкласти вектор  за базисом. Наприклад,
за базисом. Наприклад,
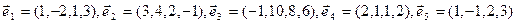 .
. ; 2)
; 2) 

 ,
,  .
.
 та
та  де
де 
 на
на 



 .
. .
.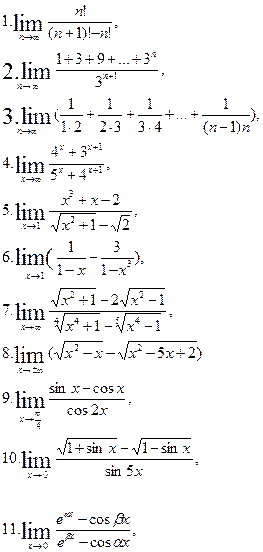
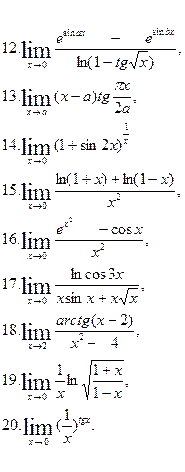
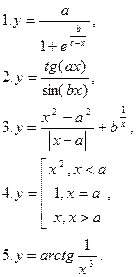
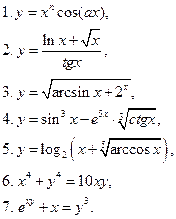











 у точці М (2;-3;1)
у точці М (2;-3;1)


