
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типове завдання індивідуальної роботи №2Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
З ТЕОРІЇ ЙМОВІРНОСТЕЙ
Варіант № 00
1. Задано ряд розподілу випадкової величини:
Побудувати та обчислити: а) многокутник розподілу; б) функцію розподілу; в) графік функції розподілу; г) моду; д) оцінити медіану; е) математичне сподівання; є) дисперсію; ж) середнє квадратичне відхилення; з) асиметрію; и) ексцес; і) 2. В партії із 10 деталей є 7 стандартних. Навмання відібрано 3 деталі. Скласти закон розподілу дискретної випадкової величини Х – числа стандартних деталей серед відібраних. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення. 3. Випадкова величина Х задана функцією розподілу
а) обчислити параметр 4. Власник фермерського господарства вирішив застрахувати нерухомість: кам’яні будівлі на 10 тис. гр., а дерев’яні на 20 тис. гр. Зі статистичних даних відомо, що ймовірність страхового випадку на кам’яних будівлях складає 0,0001, а на дерев’яних – 0,0002. Яку суму повинен сплатити фермер страховій компанії, якщо вона повинна дорівнювати середнім збиткам компанії? 5. Випадкова величина Х нормально розподілена з математичним сподіваням М(Х)= -1 і дисперсію D(X)=10. Записати вирази для щільності розподілу ймовірностей f(x) та функції розподілу F(x) і побудувати їх графіки. Обчислити ймовірність попадання випадкової величини на проміжок [-4,2]. Яка ймовірність відхилення випадкової величини від її математичного сподівання більше, ніж на 2 одиниці? 6. Система випадкових величин (
Знайти: а) двовимірну функцію розподілу, б) ряди розподілу кожної випадкової величини, в) одновимірні функції розподілу, г) числові характеристики системи: математичне сподівання, дисперсію, кореляційний момент, д) умовне математичне сподівання випадкової величини
ТИПОВІ ТЕСТОВІ ЗАВДАННЯ ПОТОЧНОГО КОНТРОЛЮ ЗНАНЬ СТУДЕНТІВ ЗА ТЕМОЮ: ВИПАДКОВІ ВЕЛИЧИНИ , 1. 1. Д (Х-У)= а; Д(Х) – Д(У) -? 2. Д(Х) + Д(У) -?, якщо Х, У – незалежні 3. Д(Х) +Д(У)+2Кху.
4. А і В – незалежні 1. Р (АВ) = Р(А)·Р(В); 2. Р(АВ)=Р(А) ·РА(В); 3. Р(АВ)=Р(В)·РВ(А).
3. Х- дискретна в.в. 1. М(Х) = 2. 3.
ТИПОВІ ТЕСТОВІ ЗАВДАННЯ ПОТОЧНОГО КОНТРОЛЮ ЗНАНЬ СТУДЕНТІВ ЗА ТЕМОЮ: ЧИСЛОВІ ХАРАКТЕРИСТИКИ В.В. 1. Задано закон розподілу ДВВ
а) 1) а = 0,3 б) 1) 5<M(x)<7 в) 1) 2) а = 0,4 2) M(x)<5 2) 3) а = 0,5 3) M(x)=5 3)
2.
1) М(х) =N; 1) D(x) = N2 +2,2; 2) M(x)<N; 2) D(x)=2,2; 3) M(x)>N; 3) D(x)= N2 –2,2. ЗАВДАННЯ ДЛЯ ЛАБОРАТОРНИХ РОБІТ З РОЗДІЛУ МАТЕМАТИЧНА СТАТИСТИКА Лабораторна робота № 1
У ста випадково обраних пунктах обміну валюти було зафіксовано дані про курс продажу долара. Було отримано наступну вибірку: 5.2 5.1 5.0 5.0 5.0 5.0 5.4 5.4 5.2 5.2 4.6 5.0 4.7 5.1 5.0 5.0 4.8 5.4 4.8 5.0 5.2 5.1 4.9 4.6 4.9 5.1 5.2 4.9 4.7 4.9 5.0 4.6 4.7 5.1 4.9 4.8 4.9 5.2 4.6 5.1 5.0 5.3 5.1 5.1 4.9 5.3 4.6 4.9 4.8 5.0 5.0 5.0 5.0 5.0 5.3 5.2 5.0 5.1 4.7 5.0 5.0 4.9 4.8 5.1 4.8 4.9 5.1 5.1 4.8 4.7 5.2 4.8 4.8 4.9 5.2 4.8 5.1 5.0 5.3 5.0 5.1 4.9 5.3 4.8 4.9 4.8 5.0 5.1 5.1 5.1 4.8 4.7 4.9 5.1 5.2 4.9 4.7 4.9 4.8 5.0
На основі приведених вибіркових даних: 1. Знайти середнє значення курсу долара 2. Розбиваючи на дев’ять рівних інтервалів побудувати інтервальний ряд. 3. Згідно інтервальному ряду побудувати гістограму розподілу відносних частот. 4. За критерієм Пірсона перевірити з рівнем значущості а) a = 0,01, б) a = 0,05 гіпотезу про нормальний закон розподілу у сукупності. 5. У випадку, якщо вибіркові дані відповідають нормальному закону розподілу, з надійністю а) 0,95, б) 0,99 знайти довірчий інтервал для
Лабораторна робота № 2
В таблиці записані статистичні дані з п’ятнадцяти ділянок про урожайність зернових Y в залежності від кількості добрив X.
На основі приведених даних потрібно: 1. Виявити кореляційно - регресійну залежність урожайності від кількості добрив; обчислити числові характеристики: вибірковий кореляційний момент та коефіцієнт кореляції. 2. На координатній площині побудувати точки (хі, уі). Проаналізувати, чи існує лінійна залежність між випадковими величинами X та Y. 3. Знайти рівняння лінії регресії та за цим рівнянням побудувати графік прямої. 4. Скориставшись знайденим рівнянням лінії регресії знайти (спрогнозувати) якою буде урожайність, якщо кількість добрив прийме наступне значення: а) х= 7,5; б) х= 32.
ВКАЗІВКИ ПО ВИКОНАННЮ ТИПОВИХ ЗАВДАНЬ ПОТОЧНОГО ТА ПІДСУМКОВОГО КОНТРОЛЮ ЗНАНЬ СТУДЕНТІВ З РОЗДІЛУ «МАТЕМАТИЧНА СТАТИСТИКА»
1. Записати емпіричну функцію розподілу для вибірки, яка представлена статистичним рядом:
Розв’язання: Емпіричною функцією розподілу де n- обсяг вибірки, nх- число значень випадкової величини Х у вибірці, які менші за х. Тоді запишемо емпіричну функцію розподілу
2. Побудувати гістограму частот для інтервального статистичного ряду
Розв’язання: Знайдемо суму частот вибірки: Нижче, на рисунку зображена гістограма. При цьому, основа кожного прямокутника дорівнює довжині інтервалу
3. Протягом 10 днів в банку фіксували кількість підписаних договорів за один день. Отримали наступну вибірку: 15, 20, 14, 17, 15, 22, 18, 17, 20, 21. Знайти вибіркове середнє, вибіркову дисперсію та незміщену вибіркову дисперсію для кількості підписаних договорів за один день. Розв’язання: Для знаходження вибіркового середнього скористаємось формулою (2):
Вибіркову дисперсію знайдемо за формулою (4):
Незміщена (виправлена) вибіркова дисперсія:
4. Із сукупності, що розподілена за нормальним законом зроблена вибірка об’єму Розв’язання: За формулою (9) знайдемо t
З нерівності (8) отримаємо такий довірчий інтервал: для випадку а): для випадку б): Отже, при збільшенні дисперсії довірчий інтервал збільшується, а отже точність оцінки зменшується. У випадку а) б)
5. Для даного інтервального статистичного ряду перевірити гіпотезу про нормальний закон розподілу при рівні значущості
Розв’язання: Перевіримо цю гіпотезу, скориставшись критерієм Пірсона. Нормальний закон розподілу залежить від двох параметрів:
Отже Для нормального закону розподілу ймовірність попадання випадкової величини Х на інтервал знаходять за формулою:
де
Потім складаємо порівняльну таблицю чисел: статистичних частот
За формулою (13) визначаємо міру відхилення емпіричних частот від теоретичних:
Визначимо за формулою (14) число степенів свободи: k =7-2-1=4. За таблицею 3 знайдемо критичне значення критерію при рівні значущості Відповідь: оскільки спостережене значення критерію менше ніж критичне, то гіпотеза про нормальний закон розподілу приймається. 6. В таблиці представлені статистичні дані про капітальні вкладення Х (в тис. грн..) і чистий дохід У (в тис. грн..). Знайти рівняння лінії регресії.
Розв’язання: Спочатку знайдемо числові характеристики (вибіркове середнє, дисперсію, середнє квадратичне відхилення) окремо для випадкової величини Х та У.
Тоді відповідні середньоквадратичні відхилення будуть
Оскільки так як дані таблиці не повторюються, то для обчислення кореляційного моменту скористаємось формулою (15). В даному випадку будемо мати:
Підставимо знайдені значення в рівняння (18) і отримаємо:
Отже, рівняння лінії регресії має вигляд КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ (денна форма) Кафедра вищої математики Навчальний предмет теорія ймовірностей та математична статистика Спеціальність Семестр 2 Екзаменаційний білет № Завдання 1 а) розв’яжіть рівняння б) Біноміальний закон розподілу. У виробництві деякої продукції третій сорт становить 25%. Знайти ймовірність того, що з семи навмання взятих виробів цієї продукції не менше ніж три будуть третього сорту. Завдання 2 а) Закон розподілу дискретної випадкової величини. Випадкова велична Х має такий закон розподілу
Побудувати полігон розподілу, функцію розподілу та її графік. Знайти б) Обчислити a, M(x), D (x), якщо
Завдання 3 а) Біноміальний закон розподілу дискретної випадкової величини. Ймовірність укладання угоди за результатами ділових переговорів дорівнює 0,7. Випадкова величина Х – число укладених угод після 4 ділових зустрічей. Знайти закон розподілу випадкової величини. Знайти б) Щільність розподілу неперервної випадкової величини має вигляд
Знайти параметр С, та Завдання 4 а) Задано таблицю розподілу системи двох випадкових величин
Обчислити кореляційний момент системи випадкових величин.
б) Щільність розподілу функції випадкового аргументу. Задано
Завдання 5 а) Середнє квадратичне відхилення вибірки. За даними вибірки знайти вибіркову середню і середнє квадратичне відхилення. 0;1;0;2;3;1;2;1;3;0;1;2;1;3;1;2;0;1;2;3. б) Маємо дані про розміри основних фондів на випадково вибраних підприємствах 3,8,1,35,42,03,23,31,43,72,73,92,06,15,5,25,53,93,24,84,34,12,2 Побудуйте інтервальний статистичний ряд Завдання 6 а) З великої кількості електричних ламп зроблена вибірка б) За двовимірним статистичним розподілом вибірки
Записати рівняння регресії:
Затверджено на засіданні кафедри вищої математики протокол №___ від__________ Зав. кафедрою__________Макаренко О.І. Екзаменатор_______________
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.82.108 (0.008 с.) |



 ; б) побудувати графік функції розподілу; в) знайти щільність розподілу та намалювати її графік; г) обчислити числові характеристики: моду, медіану, математичне сподівання, дисперсію, середнє квадратичне відхилення, асиметрію, ексцес; д) знайти ймовірність
; б) побудувати графік функції розподілу; в) знайти щільність розподілу та намалювати її графік; г) обчислити числові характеристики: моду, медіану, математичне сподівання, дисперсію, середнє квадратичне відхилення, асиметрію, ексцес; д) знайти ймовірність 
 ) задана таблицею розподілу.
) задана таблицею розподілу.
 , якщо випадкова величина
, якщо випадкова величина  набула значення –2,
набула значення –2,  - кількість букв у прізвищі.
- кількість букв у прізвищі. М(кХ)=КМ(Х)
М(кХ)=КМ(Х) , М(кХ)=КМ(Х)
, М(кХ)=КМ(Х) , М(кХ)=М(Х).
, М(кХ)=М(Х).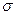 (x)=2,194
(x)=2,194 , а також наступні числові характеристики вибіркової сукупності:
, а також наступні числові характеристики вибіркової сукупності: 
 .
. називається функція, яка має вигляд
називається функція, яка має вигляд  ,
,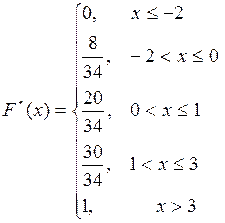
 .
. , а висота дорівнює
, а висота дорівнює  .
.

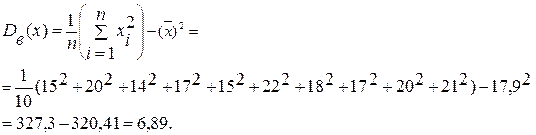 =
= .
. . З надійністю
. З надійністю  знайти довірчий інтервал для математичного сподівання а, якщо дисперсія дорівнює а)
знайти довірчий інтервал для математичного сподівання а, якщо дисперсія дорівнює а)  , б)
, б)  . Як зміниться довірчий інтервал, якщо об’єм вибірки збільшиться. Розв’язати задачу для випадку
. Як зміниться довірчий інтервал, якщо об’єм вибірки збільшиться. Розв’язати задачу для випадку  .
. . Тоді з таблиці 2 знайдемо число t=1,96.
. Тоді з таблиці 2 знайдемо число t=1,96.

 отримаємо наступні довірчі інтервали:
отримаємо наступні довірчі інтервали:

 = 0.05.
= 0.05.
 та
та 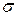 . Замінимо ці параметри їх відповідними точковими оцінками
. Замінимо ці параметри їх відповідними точковими оцінками  . Для цього знайдемо вибіркове середнє та вибіркову дисперсію, причому за представника кожного інтервалу візьмемо його середину:
. Для цього знайдемо вибіркове середнє та вибіркову дисперсію, причому за представника кожного інтервалу візьмемо його середину:

 .
.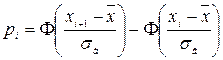 ,
, - функція Лапласа (див. Таблицю 2). Знайдемо значення теоретичних частот
- функція Лапласа (див. Таблицю 2). Знайдемо значення теоретичних частот  для кожного інтервалу. Покажемо як це робиться на прикладі третього інтервалу:
для кожного інтервалу. Покажемо як це робиться на прикладі третього інтервалу:
 (
( ).
). .
. :
:  .
.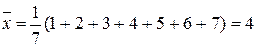 ,
,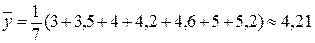 ,
, ,
, .
. ,
,  .
. . Тоді вибірковий коефіцієнт кореляції знайдемо за формулою (17):
. Тоді вибірковий коефіцієнт кореляції знайдемо за формулою (17): .
. .
. .
.
 .
.


 .
.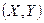
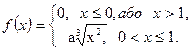 Знайти g (y), якщо Y=x2
Знайти g (y), якщо Y=x2 , обчисліть
, обчисліть 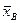 та побудуйте гістограму.
та побудуйте гістограму. . Середній час горіння ламп із вибірки виявився рівним 10000 годин. З надійністю
. Середній час горіння ламп із вибірки виявився рівним 10000 годин. З надійністю 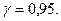 Знайти довірчий інтервал для середнього часу горіння електролампи а, якщо його
Знайти довірчий інтервал для середнього часу горіння електролампи а, якщо його  год.
год.



