
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Міністерство освіти і науки, молоді та спорту україниСодержание книги
Поиск на нашем сайте
МІНІСТЕРСТВО ОСВІТИ і НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
ДВНЗ «КИІВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ Імені В. Гетьмана» КАФЕДРА ВИЩОЇ МАТЕМАТИКИ
ЗАТВЕРДЖУЮ: ПРОРЕКТОР з науково-педагогічної роботи Колот А.М.
____ ____________ 2012 р.
МЕТОДИЧНІ МАТЕРІАЛИ щодо змісту та організації самостійної роботи студентів, Поточного і підсумкового контролю їх знань з науки “Математика для економістів”: ВИЩА МАТЕМАТИКА, ТЕОРІЯ ЙМОВІРНОСТЕЙ ТА МАТЕМАТИЧНА СТАТИСТИКА Укладачі: проф. Макаренко О.І., доц. Лісовська В.П. Затверджено на засіданні кафедри від 03.05.2012, протокол № 10 Завідувач кафедри _______________ проф. Макаренко О.І. ____ ___________ 2012 р. Погоджено начальник науково - методичного відділу _______________ Гуть Т.В. ____ _________ 2012 р.
Шановні панове – студенти та викладачі! Просимо вас ознайомитись з переліком теоретичних питань, Що охоплюють зміст робочої програми, прикладами типових Практичних завдань, змістом та порядком поточного та підсумкового контролю знань та зразками екзаменаційних білетів! Бажаємо успіхів!
ПЕРЕЛІК ПИТАНЬ, ЩО ВХОДЯТЬ ДО ПРОГРАМИ КУРСУ
І СЕМЕСТР Розділ 1. ЛІНІЙНА АЛГЕБРА 1. Означення матриці та дії над матрицями. 2. Визначники першого, другого та третього порядків. 3. Властивості визначника. 4. Мінори та алгебраїчні доповнення. Визначники n -го порядку. 5. Правило Крамера. 6. Обернена матриця. Розв’язування системи рівнянь за допомогою оберненої матриці. 7. Ранг матриці. Методи його обчислення. 8. Теорема Кронекера - Капеллі. 9. Метод Гаусса–Жордана. 10. n – вимірний векторний простір. Лінійна залежність та незалежність векторів. 11. Поняття базису n – вимірного векторного простору. Розкладання вектора за базисом. 12. Власні числа та власні вектори матриці. 13. Поняття про квадратичні форми. Визначеність квадратичної форми. 14. Застосування лінійної алгебри в економіці: модель Леонтьєва багатогалузевої економіки. 15. Матрична модель міжгалузевого балансу в натуральному (або вартісному) виразі. 16. Лінійні моделі оптимального планування.
Розділ 2. АНАЛІТИЧНА ГЕОМЕТРІЯ 17. Системи координат та їх перетворення.
18. Найпростіші задачі аналітичної геометрії. 19. Вектори, лінійні операції над векторами. 20.Проекція вектора на вісь та її властивості. 21. Скалярний, векторний і мішаний добутки векторів та їх властивості. 22. Поняття рівняння лінії в R2. 23. Рівняння прямої з кутовим коефіцієнтом. В”язка прямих. 24. Кут між прямими. Умови паралельності та перпендикулярності прямих. 25. Загальне рівняння прямої та його дослідження. 26. Рівняння прямої що проходить через дві задані точки. 27. Рівняння прямої у відрізках на осях. 28. Відстань від точки до прямої. 29. Коло, його означення та рівняння. 30.Еліпс, гіпербола, парабола: їх означення, канонічні рівняння та дослідження. 31. Загальне рівняння площини та його дослідження. 32. Рівняння площини що проходить через три точки. 33. Рівняння площини у відрізках на осях. 34.Віддаль від точки до площини. 35. Пряма лінія в просторі. 36. Задача про рівновагу доходів та збитків компанії. 37. Моделі рівноваги ринку при умові, що функції попиту та пропозиції лінійні.
Розділ 3. ОСНОВИ МАТЕМАТИЧНОГО АНАЛІЗУ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ 38. Поняття послідовності та її границі. 39. Властивості збіжних послідовностей. 40. Нескінченно великі та нескінченно малі величини, їх властивості, зв’язок між ними. 41. Теореми що полегшують знаходження границь. 42. Число e. Економічна інтерпретація числа e. 43. Поняття границі функції.Теореми про границі. 44. Розкриття невизначеностей для алгебраїчних функцій. 45. Особливі границі. 46. Шкала нескінченно малих величин та їх застосування. 47. Неперервність функції в точці та на проміжку. 48. Властивості неперервних функцій. 49. Точки розриву функції та їх класифікація. 50. Задачі доходу із дослідженням на неперервність. 51. Похідна функції. Фізичний, геометричний, економічний зміст. Задача про продуктивність праці. 52. Правила диференціювання. 53. Похідна оберненої функції. 54. Похідна показникової, логарифмічної, степеневої, тригонометричних та обернених тригонометричних функцій. 55. Рівняння дотичної та нормалі до графіка функцій. 56. Таблиця похідних. 57. Похідна неявної функції. 58. Похідна степенево- показникової функції. 59. Еластичність функції. 60. Диференціал функції.
61. Правила обчислення диференціалів. Інваріантність форми першого диференціала. 62. Похідні та диференціали вищих порядків. 63. Теореми Ферма, Ролля, Лагранжа, Коші. 64. Правило Лопіталя. 65. Формула Тейлора. 66.Теорема про сталість функції на проміжку. 67. Умови зростання та спадання функції на проміжку.. 68. Екстремуми функції. Необхідна та достатня умови. 69. Опуклість функції: означення та достатні умови. 70. Точки перегину: необхідна та достатня умови. 71. Асимптоти функції, їх рівняння та властивості. 72. Алгоритм дослідження функцій та побудова їх графіків. 73. Найбільше та найменше значення функції на відрізку. ІІ СЕМЕСТР Розділ 6. ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ 108.Основні поняття про диференціальні рівняння та їхні розв’язки. 109. Задача Коші. Теорема існування та єдиності розв’язків. 110. Диференціальні рівняння з відокремленими та відокремлюваними змінними. 111. Лінійні диференціальні рівняння першого порядку. 112. Однорідні диференціальні рівняння першого порядку. 113. Економічні задачі, що приводять до диференціальних рівнянь. Задача адаптації цін по Вальрасу. 114. ЛНДР 2-го порядку з сталими коефіцієнтами. 115. Різницеві рівняння.
Розділ 7. РЯДИ 116. Означення числового ряду та його збіжність. Властивості числових рядів. 117. Необхідна умова збіжності ряду. 118. Достатні умови збіжності рядів з додатніми членами. 119. Знакозмінні ряди. Абсолютна та умовна збіжність знакозмінного ряду. 120. Знакопочережні ряди. Ознака Лейбніца. 121. Степеневі ряди. Теорема Абеля. 122. Радіус, інтервал та область збіжності степеневого ряду. 123. Ряди Тейлора та Маклорена. 124. Розвинення функцій
2. Приклади типових завдань, що виносяться на іспит
1. Обчислити визначник: 1) 2. Розв’язати систему рівнянь за формулами Крамера:
3. Виконати дії: 1)
4. Для матриці А знайти обернену та перевірити результат: 1) 5. Розв”язати систему рівнянь за допомогою оберненої матриці:
6. Розв’язати матричні рівняння 1) 2) 7. Обчислити ранг матриці
8. Дослідити систему рівнянь на сумісність
9. Розв’язати систему рівнянь методом Гаусса – Жордана
10. Довести, що вектори
11. Встановити кількість лінійно незалежних векторів для даної системи векторів
12. Знайти власні числа та власні вектори матриці: 1) 13. Встановити визначеність квадратичної форми:
14. Задана матриця А прямих матеріальних витрат та матриця В кін-цевої продукції
Знайти необхідний обсяг валового випуску (модель Леонтьєва):
15. Паралелограм побудовано на векторах Знайти: 1.Довжину діагоналей паралелограма; 2. Кут між діагоналями; 3. Площу паралелограма; 4. Проекцію 16. Дано трикутник АВС: А (3,2), В (-1,0), С (2,-3). Знайти рівняння: 1. сторони АВ; 2. медіани АЕ; 3. бісектриси СР; 4. висоти ВК; 5. середньої лінії МН що паралельна ВС. Обчислити довжини: 1. сторони АВ; 2. медіани АЕ; 3. бісектриси СР; 4. висоти ВК. Обчислити: 1. Площу трикутника АВС; 2. Кут між медіаною АЕ та бісектрисою СР. 17. Дано ОАВС – піраміда. О (5,-9,-1), А (5,1,2), В (-4,-3,6), С (-9,6,7). Знайти рівняння: 1. грані ОАВ; 2. ребра АО; 3. висоти ОК; 4. площини, що проходить через ребро АО перпендікулярно до основи. Обчислити: 1. площу основи АВС; 2. об’єм піраміди; 3. довжину висоти;
4. кут між ребрами АО та ОВ; 5. віддаль від ребра АО до сторони основи ВС. 18. Задано рівняння кола Знайти: 1. координати центра та довжину радіуса; 2. найкоротшу віддаль від точки М (3,9) до кола; 3. рівняння дотичної із точки К (-5,8) до кола. 19. Знайти ексцентриситет та координати фокусів: 1. еліпса 2. гіперболи 20. Знайти кут між асимптотами гіперболи 21. Знайти область визначення функції
22. Обчислити границі:
23. Встановити характер точок розриву функцій
24. Знайти похідну функції:
25. Знайти диференціал функції:
26. Знайти похідну другого порядку
27. Знайти екстремуми та інтервали монотонності функції:
28. Знайти точки перегину та інтервали напряму опуклості функції:
29. Знайти асимптоти графіка функції
30. Знайти найбільше та найменше значення функції на проміжку [-1;2]. 31. Знайти аналітично та дати геометричну інтерпретацію області визначення функції
32. Знайти повний диференціал функції
33. Знайти частинні похідні функції
34. Знайти частинні похідні другого порядку функції
35. Знайти кут між градієнтами функції В точках (-1;3) і (3;-3). 36. Знайти похідну функції ІІ СЕМЕСТР 40. Знайти інтеграли
41. Обчислити визначені інтеграли
42. Обчислити невластиві інтеграли або встановити їх розбіжність,
43. Знайти площу фігури, що обмежена лініями:
44. Обчислити об’єм тіла, утвореного обертанням навколо осі Оу фігури, Що обмежена лініями
45. Обчислити подвійний інтеграл
46. Розв’язати диференціальні рівняння:
47. Дослідити на збіжність ряди: 1. 2. 3. 4.
48. Знайти область збіжності степеневого ряду:
І СЕМЕСТР
Контрольна робота №1
1. Обчислити визначник
3. Роз’вязати систему та знайти загальний і базисний розв’язки
4. Знайти власні числа матриці
5. Дослідити визначеність квадратичної форми
Контрольна робота №2 1. Рівняння площини, що проходить через задану точку перпендикулярно до заданого вектора.
2. Кут між векторами
3. Задані рівняння основ трапеції:
4. Знайти рівняння гіперболи, що має спільні фокуси з еліпсом
5. Записати рівняння площини, що проходить через вісь
Контрольна робота № 1
1. Дослідіть неперервність функції
2. Обчисліть границю: 3. Знайдіть границю: 4. Знайдіть еластичність функції 5. Знайдіть диференціал функції
Контрольна робота № 2
1. Знайдіть екстремум інвестиційної функції рівноваги 2. Знайдіть граничну норму заміщення
3. Знайдіть градієнт функції 4. Знайдіть екстремум функції 5. Побудуйте область визначення функції
ІІ СЕМЕСТР Модуль № І
Контрольна робота №1 Знайти невизначені інтеграли: 1. 4. Контрольна робота №2 1. 4. 5.
Модуль № ІІ
Контрольна робота №1 1. Знайти загальний розв’язок диференціального рівняння (ДР):
2. Знайти частинний розв’язок ДР 3. Знайти частинний розв’язок ДР 4. Знайти частинний розв’язок ЛО ДР 5. Знайти загальний розв’язок ДР
Контрольна робота №2 1. Знайти суму ряду
2. Дослідити на збіжність ряд
3. Дослідити на збіжність (абсолютну чи умовну) ряд
4. Розвинути в ряд за степенями х функцію
5. Знайти область збіжності ряду
Картка самостійної роботи студентів З дисципліни “Математика для економістів: вища математика” (денна форма)
Результати поточного контролю знань студентів в цілому оцінюють в діапазоні від 0 до 50 балів. * Студент отримує: 1) 5 балів за умови виконання домашньої роботи та відповіді в аудиторії (усно, тести, розв’язування задач біля дошки, тощо) на оцінку «відмінно» (в середньому за тему); 2) 4 бали – відповідь на «добре» з виконанням домашнього завдання (в середньому за тему); 3) 3 бали – відповідь на «задовільно» з виконанням домашнього завдання;
4) 1 бал - відповідь на «незадовільно» з виконанням домашнього завдання; 5) 0 балів – відповідь на «незадовільно» без виконаного домашнього завдання. Картка самостійної роботи студентів З дисципліни “Математика для економістів: вища математика” (денна форма)
Результати поточного контролю знань студентів в цілому оцінюють в діапазоні від 0 до 60 балів, але у відомість виставляється оцінка не вище 50балів. * Студент отримує: 1) 5 балів за умови виконання домашньої роботи та відповіді в аудиторії (усно, тести, розв’язування задач біля дошки, тощо) на оцінку «відмінно» (в середньому за тему); 2) 4 бали – відповідь на «добре» з виконанням домашнього завдання (в середньому за тему); 3) 3 бали – відповідь на «задовільно» з виконанням домашнього завдання; 4) 1 бал - відповідь на «незадовільно» з виконанням домашнього завдання; 5) 0 балів – відповідь на «незадовільно» без виконаного домашнього завдання.
2.2.9 ПОРЯДОК ПОТОЧНОГО І ПІДСУМКОВОГО КОНТРОЛЮ ЗНАНЬ СТУДЕНТІВ З ВИЩОЇ МАТЕМАТИКИ. КРИТЕРІЇ ОЦІНКИ. Завданням поточного контролю є перевірка розуміння та засвоєння певного матеріалу, вироблених навичок, проведення розрахункових робіт, умінь самостійно розв‘язувати задачі, здатності осмислити зміст теми чи розділу у взаємозв’зку з іншими темами. Завданням іспиту є перевірка розуміння студентом програмного матеріалу в цілому, логіки та взаємозв‘язків між окремими розділами, здатності творчого використання накопичених знань для розв‘язання задач. Оцінювання здійснюється за 100 бальною шкалою. Завдання поточного контролю оцінюються в діапазоні від 0 до 50 балів, а завдання, що виносяться на іспит – від 0 до 50 балів.
ПОТОЧНИЙ КОНТРОЛЬ ЗНАНЬ СТУДЕНТІВ Об‘єктами поточного контролю знань студента є: 1) системність та активність роботи на практичних заняттях; 2) виконання завдань для самостійного опрацювання; 3) виконання модульних завдань.
1. При контролі систематичності та активності роботи на практичних заняттях оцінці підлягають: а) рівень знань, продемонстрований у відповідях - тестах на практичних заняттях; за кожне практичне заняття та виконання домашнього завдання студент отримує max 5 б; по завершенні вивчення теми в електронний журнал проставляється середній бал за тему від 0 до 5 балів (ці бали можуть бути розподілені на декілька занять в електронному журналі) в) участь в роботі наукових студентських конференцій, олімпіадах, підготовка наукових публікацій тощо (за рішенням кафедри) – не більше 10 балів у сумі, (якщо при цьому загальна кількість балів за поточну роботу не перевищує 50 балів). 2. При контролі виконання завдань для самостійного опрацювання оцінці підлягають самостійне опрацювання тем в цілому чи окремих питань зі звітом у вигляді: а) проведення розрахунків (розв’язування певних задач за своїм варіантом) - не більше 10 балів – І семестр та ІІ семестр. б) виконання індивідуальних завдань. Оцінка за одну індивідуальну роботу не перевищує 5 балів у І та ІІ семестрах. в) написання рефератів (у визначені терміни) – не більше 3 балів. Самостійно виконані роботи перевіряються викладачем та підлягають захисту у ході співбесіди зі студентом. 3. При виконанні модульних завдань оцінці підлягають: а) виконання письмових завдань під час проведення контрольних робіт. Оцінка за цей вид контролю співпадає з кількістю балів за контрольну роботу за 6 бальною шкалою (0; 1; 2; 3; 4; 5). Контрольна робота повинна проводитися в аудиторії без допущення викладачем користування допоміжними матеріалами. Модуль з вищої математики – це частина програми, яка складається з пов‘язаних між собою у певному співвідношенні теоретичних і практичних компонентів змісту, кожна складова якого оцінюється в балах. За семестр з вищої математики проводиться 2 модуля (кожний по 2 контрольні роботи). Результати поточного контролю знань студентів в цілому оцінюють в діапазоні від 0 до 50 балів за І семестр та ІІ семестри. Всі види самостійно виконаних домашніх письмових робіт перевіряються викладачем та підлягають захисту у ході співбесіди зі студентом. В разі невиконання завдань поточного контролю з об‘єктивних причин студент має право, за дозволом декана, виконати їх і скласти залік до останнього практичного заняття. Час та порядок виконання визначає викладач. 4. Підсумковий контроль знань студентів у формі іспиту Оцінювання знань студентів з вищої математики з підсумковим контролем - іспит здійснюється на основі результатів поточного і підсумкового контролю знань (іспиту). Об‘єктом контролю знань студентів у формі іспиту є результати виконання письмових екзаменаційних завдань. На іспит виносяться вузлові питання, типові та комплексні задачі, ситуації, завдання, що потребують творчої відповіді та уміння синтезувати отримані знання і застосовувати їх при вирішенні практичних задач тощо. Перелік питань, що охоплюють зміст програми з вищої математики, критерії оцінювання екзаменаційних завдань визначаються кафедрою, включаються до робочої програми дисципліни і доводяться до студентів на початку семестру. Екзаменаційний білет містить 6 завдань відповідно до пройдених тем, кожне з яких оцінюється за шкалою 10; 8; 6; 0 балів. Кожне завдання містить два приклади, тести чи задачі. Результати іспиту в діапазоні від 0 до 60 балів (включно). Зауваження. 10 балів виставляється за правильне розв’язання завдання, тобто розв’язок завдання не має жодної суттєвої помилки; 8 - якщо розв’язання має не суттєву помилку. Не суттєвою помилкою вважається помилка обчислювального характеру, що приводить до невірної відповіді. Якщо розв’язуване завдання містить недоліки, або вірно розв’язано один пункт із завдання, то завдання оцінюється в 6 балів. Недоліком вважаються такі дії, перетворення чи записи, що не приводять до суттєвих помилок. Неправильно виконане завдання оцінюється в 0 балів. В разі, коли відповіді студента оцінені менше ніж в 30 балів, він отримує незадовільну оцінку за результатами іспиту та незадовільну загальну підсумкову оцінку. Загальна підсумкова оцінка з вищої математики складається з суми балів за результатами поточного контролю знань та за виконання завдань, що виносяться на іспит (за умови, що студент набрав 30 балів і вище), але не перевищує 100 балів. До екзаменаційної відомості заносяться сумарні результати в балах поточного контролю та іспиту. Переведення даних 100-бальної шкали оцінювання в 4-х бальну здійснюється в такому порядку: Оцінка “відмінно” – 90-100 балів. Оцінка “добре” – 70-89 балів. Оцінка “задовільно” – 60-69 балів. Оцінка “незадовільно” – менше 60 балів. Оцінка за 4-и бальною шкалою оцінювання виставляється в заліково-екзаменаційній відомості поряд із загальною підсумковою оцінкою в 100-бальній шкалі. Складання академічної заборгованості студентами всіх форм навчання з вищої математики, що виноситься на іспит, передбачає виконання модульних (контрольних) завдань, та екзаменаційних завдань, і проводиться згідно “Положення про організацію навчального процесу в умовах його індивідуалізації та впровадження кридитно- модульної системи”, затвердженим Вченою радою університету (протокол № 9 від 30.03.2006 р.) та Ухвали Вченої ради університету від 30.09.2004 р. (Протокол №2) зі змінами та доповненнями, затвердженими Ухвалою Вченої ради КНЕУ від 28.04.2005р. (Протокол №9) та Ухвали Вченої Ради «Про нову редакцію Порядку оцінювання знань студентів» від 28.05.2009 р. СТУДЕНТІВ ЗАОЧНОЇ ФОРМИ НАВЧАННЯ
1. Об‘єктом поточного контролю знань студентів заочної форми навчання є домашня контрольна робота, що складена із індивідуальних завдань. 2. Контрольні роботи, виконані самостійно перевіряються викладачем та підлягають захисту у ході співбесіди зі студентом. 3. Результати поточного контролю знань студентів, вносяться до залікової екзаменаційної відомості. Підсумковий контроль знань студентів – заочників – у вигляді іспиту у І та другому семестрах. Завдання для поточного контролю знань студентів Заочної форми навчання. Для студентів – заочників кафедрою вищої математики розроблена допоміжна література, яка знаходиться у бібліотеці 5к. КНЕУ (вул. Мельникова 81): 1. “Збірник завдань для контрольних робіт №1,2” для студентів заочної форми навчання. 2. “Розв’язування завдань для контрольних робіт №1,2” для студентів заочної форми навчання за 2006р. В контрольній роботі за І семестр виконуються наступні завдання із [2]: 1.1, 1.2, 1.3, 1.5, 2.1, 2.2, 2.4, 3.1, 3.1.1, 3.1.2, 3.1.3, 4.1, 4.2. В контрольній роботі за ІІ семестр виконуються наступні завдання із [2]: 5.3,5.4, 6.2, 6.3, 6.4, 6.7, 7.1, 7.3, 8.1, 8.3. Варіант відповідного завдання визначається за двома останніми цифрами залікової книжки.
5. Зразок екзаменаційного білета. Екзаменаційний білет №1 Завдання 1 А).Обчислити визначник: Б).Дослідити систему лінійних алгебраїчних рівнянь на сумісність та знайти загальний та базисний розв’язки: Завдання 2 А). Обчислити Б). Для трикутника з вершинами О(0; 0), А(8; 0) та В(0; 6) написати рівняння медіани ОС та знайти її довжину. Завдання 3 Обчислити границі: А) Б). Дослідити на неперервність функцію: Завдання 4 А). Знайти Б).Знайти еластичність функції Завдання 5 А). Знайти градієнт функції Б). Знайти екстремуми функції Завдання 6 А).Розв’язати рівняння
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.85.59 (0.016 с.) |


 у ряд Маклорена.
у ряд Маклорена.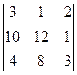 , 2)
, 2)  .
. .
.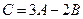 , 2)
, 2)  , якщо
, якщо .
. , 2)
, 2)  .
.
 ,
,  ,
,  , якщо:
, якщо:

 .
. .
. .
. утворюють базис та розкласти вектор
утворюють базис та розкласти вектор  за базисом. Наприклад,
за базисом. Наприклад,
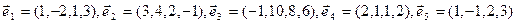 .
. ; 2)
; 2) 

 ,
,  .
.
 та
та  де
де 
 на
на 



 .
. .
.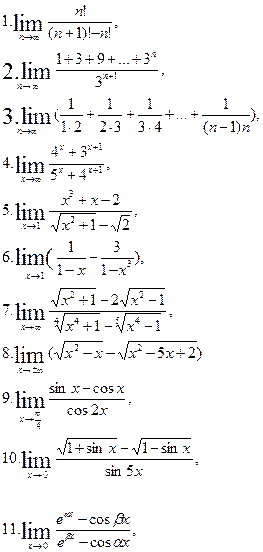
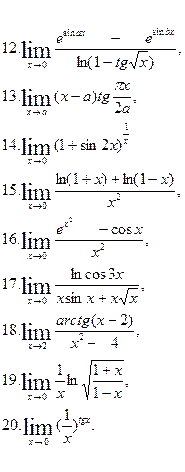
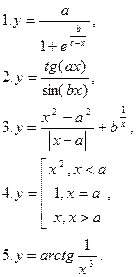
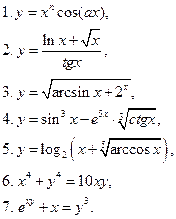











 у точці М (2;-3;1)
у точці М (2;-3;1)


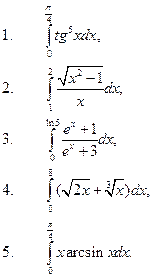
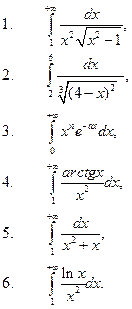










 , якщо
, якщо 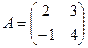 ,
,  ,
,  .
.
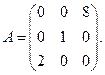
 .
. та
та  дорівнює
дорівнює  ,
,  ,
,  . Знайти коефіцієнт
. Знайти коефіцієнт  такий, щоб вектори
такий, щоб вектори  та
та  були ортогональні.
були ортогональні. та
та  . Знайти висоту трапеції.
. Знайти висоту трапеції. , ексцентриситет якої дорівнює
, ексцентриситет якої дорівнює  .
. і утворює з площиною
і утворює з площиною  кут
кут 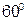 .
. .
. ;
;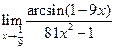 .
. .
. .
.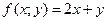 при умові
при умові .
. для функції
для функції .
. у точці
у точці  .
. .
. .
. ; 2.
; 2.  ; 3.
; 3.  ;
; ; 5.
; 5.  .
. ; 2.
; 2.  ; 3.
; 3. 
 ,де область Д обмежена лініями у=х; у= 2 х; х= 4.
,де область Д обмежена лініями у=х; у= 2 х; х= 4. де область Д - прямокутник 0 < х £ 3, 4 £ у £ 9.
де область Д - прямокутник 0 < х £ 3, 4 £ у £ 9.

 при заданих початкових умовах
при заданих початкових умовах  .
. при заданих початкових умовах
при заданих початкових умовах 
 якщо
якщо  при
при  .
.





 .
.
 , якщо
, якщо  ,
,  , кут між векторами
, кут між векторами  .
. ,
, .
. :
:  .
. в точці х=2.
в точці х=2. в точці М(2,3).
в точці М(2,3). =
=  .
. , якщо
, якщо 




