
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачі, що приводять до поняття похідної функціїСодержание книги
Поиск на нашем сайте Базовою задачею економічного аналізу є вивчення зв’язків економічних величин, записаних у вигляді функцій. В економіці дуже часто потрібно знайти найкраще оптимальне значення того чи іншого показника: найвищу продуктивність праці, максимальний прибуток чи мінімальні витрати і т.п. Кожен показник є функцією одного чи декількох аргументів. Наприклад, випуск можна розглядати як функцію витрат праці і капіталу. Таким чином, знаходження оптимального значення показника зводиться до знаходження екстремуму (максимуму чи мінімуму) функції однієї або багатьох змінних. Подібні задачі породжують клас екстремальних задач в економіці, розв'язання яких вимагає використання методів диференціального числення. Найчастіше в економіці приходиться розв’язувати задачі на екстремум функцій багатьох змінних, оскільки економічні показники звичайно залежать від багатьох чинників. Такі задачі добре вивчені теорією функцій багатьох змінних. Багато задач містять у собі не тільки максимізуючу (мінімізуючу) функцію, але й обмеження (наприклад, бюджетне обмеження в задачі споживчого вибору). Це – задачі математичного програмування, для розв'язання яких розроблено спеціальні методи, що спираються на диференціальне числення. Важливий розділ методів диференціального числення, що використовуються в економіці, називається методами граничного аналізу. Отже, граничний аналіз в економіці – це сукупність прийомів дослідження величин, що змінюються, наприклад, витрат, або прибуток при змінах об'ємів виробництва чи споживання і т.п. на основі аналізу їхніх граничних значень. Приклад 3.1. Задача про продуктивність праці. Нехай функція Розв’язання. Очевидно, за період часу від Приклад 3.2. В практиці економічних досліджень широке застосування одержали виробничі функції, що використовуються для встановлення залежностей, наприклад, випуску продукції від витрат ресурсів, витрат виробництва від об'єму продукції, виторгу від продажу товару і т.п. У припущенні диференційованості виробничих функцій важливого значення набувають їхні диференціальні характеристики, пов'язані з поняттям похідної. Розв’язання. Розглянемо деякі типи виробничих функцій. 1). Нехай виробнича функція Припустимо, що кількість продукції збільшується на Середній приріст витрат виробництва є Граничними витратами виробництва називається границя
Граничні витрати виробництва збігаються зі швидкістю зміни витрат виробництва. Їх величина характеризує приблизно додаткові витрати на виробництво одиниці додаткової продукції. 2). Нехай
3). Нехай виробнича функція
За допомогою похідної можна обчислити приріст залежної змінної, що відповідає приросту незалежної змінної.
Поняття похідної Нехай функція Проробимо такі операції. Зафіксуємо точку
Ця границя, якщо вона існує, називається похідною функції Означення 3.1. Похідною функції Похідна функції Як випливає з означення, похідна функції Таким чином, похідна Приклад 3.3. Обчислити похідну функції Розв’язання. Зафіксуємо довільне значення аргументу
Складемо відношення приросту функції до приросту аргументу
Оскільки точка
Економічний зміст похідної. Виходячи з прикладів, розглянутих в §1, похідна функції об’єму зробленої продукції за часом Фізичний зміст похідної. Для довільної функції похідна
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.008 с.) |

 виражає кількість зробленої продукції
виражає кількість зробленої продукції 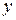 за час
за час  і необхідно знайти продуктивність праці в момент
і необхідно знайти продуктивність праці в момент  .
. кількість зробленої продукції зміниться від значення
кількість зробленої продукції зміниться від значення  до значення
до значення 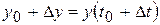 . Тоді середня продуктивність праці за цей період
. Тоді середня продуктивність праці за цей період 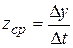 . Продуктивність праці в момент
. Продуктивність праці в момент  , тобто
, тобто  .
.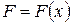 – функція витрат виробництва, що залежить від кількості продукції
– функція витрат виробництва, що залежить від кількості продукції  .
. . Кількості продукції
. Кількості продукції 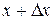 відповідають витрати виробництва
відповідають витрати виробництва 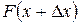 . Отже, збільшенню кількості продукції
. Отже, збільшенню кількості продукції  .
. . Це приріст витрат виробництва на одиницю збільшення кількості продукції.
. Це приріст витрат виробництва на одиницю збільшення кількості продукції.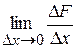 .
.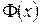 – виторг від продажу
– виторг від продажу  одиниць товару. Граничним виторгом називається границя
одиниць товару. Граничним виторгом називається границя .
. встановлює залежність випуску продукції
встановлює залежність випуску продукції 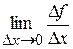 .
. і в її околі.
і в її околі.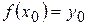 . Додамо аргументу
. Додамо аргументу  . Обчислимо приріст функції
. Обчислимо приріст функції 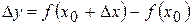 . Складемо відношення приросту функції до приросту аргументу
. Складемо відношення приросту функції до приросту аргументу  . Спрямуємо
. Спрямуємо  . (3.1)
. (3.1) в точці
в точці 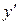 або
або  , що введені французьким математиком Лагранжем або символами
, що введені французьким математиком Лагранжем або символами  ,
, 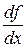 , що введені німецьким математиком Лейбніцом. Символ
, що введені німецьким математиком Лейбніцом. Символ  , підкреслюючи, що похідна обчислюється по аргументу
, підкреслюючи, що похідна обчислюється по аргументу  за означенням.
за означенням.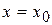 , тоді
, тоді  . Обчислимо приріст функції
. Обчислимо приріст функції
 .
. . Спрямуємо приріст аргументу
. Спрямуємо приріст аргументу  до нуля й обчислимо границю:
до нуля й обчислимо границю: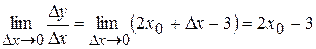 .
. .
. є продуктивність праці в момент
є продуктивність праці в момент 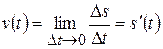 , тобто похідна за часом від функції, що визначає закон руху, дорівнює миттєвій швидкості руху точки.
, тобто похідна за часом від функції, що визначає закон руху, дорівнює миттєвій швидкості руху точки. характеризує швидкість зміни функції в даній точці залежно від зміни аргументу.
характеризує швидкість зміни функції в даній точці залежно від зміни аргументу.


