
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні правила диференціюванняСодержание книги
Поиск на нашем сайте
Нехай функції 1. Похідна алгебраїчної суми функцій дорівнює алгебраїчній сумі похідних функцій, тобто
Нехай
Остаточно одержимо 2. Похідна добутку. Доведемо, що
Нехай
Застосовуючи теореми про границю суми і добутку, будемо мати: Врахуємо, що Зокрема, якщо
тобто сталий множник можна виносити за знак похідної. Використовуючи останню формулу і похідну натурального логарифма, можна одержати похідну функції
3. Похідна частки. Розглянемо функцію
Дійсно, приріст функції, що відповідає приросту аргументу
Застосовуючи теорему про границі частки і добутку і, враховуючи неперервність функції
Приклад 3.5. Довести, що Розв’язання. Маємо:
Аналогічно виводиться формула похідної функції
Похідна складної функції Нехай Нехай функція Доведемо, що
Дамо Запишемо тотожність Наприклад, якщо
Логарифмічне диференціювання. Похідна степеневої, показникової, показниково-степеневої функцій Логарифмічне диференціювання полягає в тому, що функцію попередньо логарифмують, а потім обчислюють її похідну. Нехай функція
Зауваження. Похідна функції Розглянемо степеневу функцію
При Для показникової функції
Поклавши
Показниково-степеневою називається функція вигляду Тоді:
тобто похідна показниково-степеневої функції дорівнює сумі похідних від цієї функції, обчислених як від степеневої і як від показникової окремо. Приклад 3.6. Обчислити похідну функції Розв’язання. Для цієї функції
Похідна оберненої функції. Похідні обернених тригонометричних функцій Нехай функція Теорема 3.3. Похідні обернених функцій обернені за величиною, тобто
Дійсно, запишемо відношення Покажемо, що Дійсно, для функції
З означення функції
Аналогічно можна довести, що
Для функції За теоремою 3.3
Аналогічно
Таблиця похідних Наведемо таблицю похідних з одержаних формул для складної функції 1. 2. 3. 4. 5. 6.
7.
Приклад 3.7. Знайти похідні функцій: а) б) Розв’язання. У випадку а) У випадку б)
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 604; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.104.140 (0.007 с.) |

 і
і  мають похідні в точці
мають похідні в точці  .
. . (3.4)
. (3.4) . Дамо
. Дамо  , тоді функції
, тоді функції  і
і  одержують прирости, відповідно рівні
одержують прирости, відповідно рівні  і
і  , а функція
, а функція 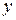 одержить приріст
одержить приріст  . Нове значення функції
. Нове значення функції 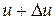 , функції
, функції  і отже
і отже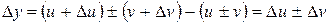 ,
,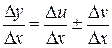 ,
,  .
. .
.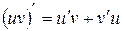 . (3.5)
. (3.5) . Дамо
. Дамо  і
і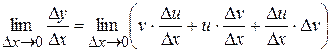 .
. .
. ,
,  ,
,  . Виходить
. Виходить 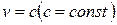
 ,
, . Враховуючи, що
. Враховуючи, що  , одержимо
, одержимо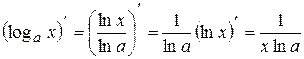 . (3.6)
. (3.6)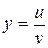 . Припустимо, що функція
. Припустимо, що функція  . (3.7)
. (3.7) ,
,  .
. ,
,  .
. .
.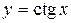 .
. ,
,  , причому область зміни другої функції входить в область визначення першої функції. Тоді
, причому область зміни другої функції входить в область визначення першої функції. Тоді  має похідну по незалежній змінній
має похідну по незалежній змінній  має похідну в точці
має похідну в точці  . (3.8)
. (3.8) і знайдемо його границю при
і знайдемо його границю при  . Якщо
. Якщо 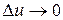 , оскільки
, оскільки  або
або 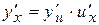 , що і було потрібно довести.
, що і було потрібно довести. , то
, то  . Тоді
. Тоді .
. має похідну при деякому значенні
має похідну при деякому значенні  і застосовуючи правило диференціювання складної функції, одержуємо:
і застосовуючи правило диференціювання складної функції, одержуємо: , звідки
, звідки  . (3.9)
. (3.9) дорівнює
дорівнює  , тобто тому ж самому виразу, що одержимо, якщо опустимо знак модуля у виразі
, тобто тому ж самому виразу, що одержимо, якщо опустимо знак модуля у виразі  і візьмемо похідну від цього логарифма формально; тоді одержимо
і візьмемо похідну від цього логарифма формально; тоді одержимо  не оберталася в нуль. Якщо
не оберталася в нуль. Якщо  , то логарифмічне диференціювання неможливе.
, то логарифмічне диференціювання неможливе. , де
, де  . При будь-якому
. При будь-якому  ,
,  ,
, 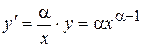 тобто
тобто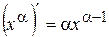 .
. маємо
маємо 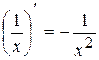 , при
, при 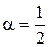 одержимо
одержимо  .
. ,
, 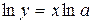 ,
,  ,
,  . Отже,
. Отже,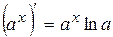 .
. , одержимо
, одержимо .
. . Нехай
. Нехай  . Обчислимо похідну функції
. Обчислимо похідну функції  . Логарифмуючи, одержимо
. Логарифмуючи, одержимо 
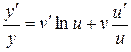 ,
,  , або звідки
, або звідки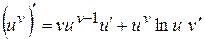 , (3.10)
, (3.10) .
. . Обчислимо похідну останньої рівності:
. Обчислимо похідну останньої рівності:  або
або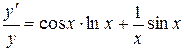 , звідки
, звідки 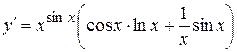 .
. , відмінну від нуля. Обернена їй функція
, відмінну від нуля. Обернена їй функція  має похідну в точці
має похідну в точці  . (3.11)
. (3.11)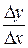 у вигляді
у вигляді  , де
, де  , оскільки функція
, оскільки функція  , що і було потрібно довести.
, що і було потрібно довести. .
.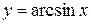 ,
,  . Знаємо, що
. Знаємо, що  , звідки на підставі теореми 3.3 одержимо
, звідки на підставі теореми 3.3 одержимо . (3.12)
. (3.12) випливає, що
випливає, що  , за цією умовою,
, за цією умовою,  , виходить,
, виходить,  . Тому
. Тому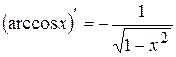 . (3.13)
. (3.13) ,
,  .
. ,
,  , звідки
, звідки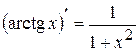 . (3.14)
. (3.14) . (3.15)
. (3.15) ,
,  .
. .
. .
.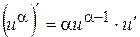 ,
,  ,
,  .
. ,
,  .
. ,
, 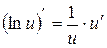 .
. ,
,  ,
, ,
,  .
.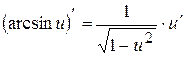 ,
, 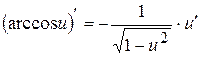 ,
,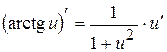 ,
,  .
. ;
; .
. .
.




