
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні теореми диференціального численняСодержание книги
Поиск на нашем сайте
Теорема Лагранжа (теорема про скінченні прирости). Якщо функція
Дана теорема має просту геометричну інтерпретацію (рис. 3.5).
Проведемо січну
Теорема Лагранжа може бути представлена у вигляді
тобто якщо функція неперервна на відрізку Для довільного відрізка
Теорема Ролля (теорема про нулі похідної). Якщо функція Справді, для функції
Геометрично теорема Ролля ілюструється просто: у точках Зокрема, якщо припустити, що Теорема Коші. Якщо кожна з двох диференційованих функцій
Зауважимо, що теорема Лагранжа є частинним випадком теореми Коші при
Правило Лопіталя Нехай для функцій Правило Лопіталя. Якщо функції
Розглянемо відрізок Тоді Нехай при
Якщо виявиться, що Приклад 3.14. Обчислити Розв’язання. Функції
Покажемо, що правило Лопіталя справедливо і за умови, якщо Нехай, наприклад, умови теореми виконуються і Поклавши Функції
звідки одержимо, що
Можна також показати, що правило Лопіталя можна застосувати й у випадку, якщо
Приклад 3.15. Обчислити Розв’язання. Для функції
Розкриття невизначеностей вигляду Приклад 3.16. Обчислити границю Розв’язання. Безпосередньою підстановкою замість
Правило Лопіталя дає можливість розкривати невизначеності вигляду
Для обчислення границі такої функції при Приклад 3.17. Обчислити Розв’язання. Нехай Отже,
|
||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.15.225 (0.008 с.) |

 неперервна на відрізку
неперервна на відрізку  і диференційована у всіх внутрішніх точках цього відрізка, то усередині відрізка
і диференційована у всіх внутрішніх точках цього відрізка, то усередині відрізка  , що
, що . (3.24)
. (3.24)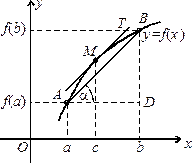 Рис. 3.5.
Рис. 3.5.
 . Координати точок
. Координати точок  і
і 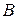 відповідно дорівнюють
відповідно дорівнюють  ,
,  і
і  ,
,  . Очевидно, що кутовий коефіцієнт січної
. Очевидно, що кутовий коефіцієнт січної  . Будемо переміщувати січну
. Будемо переміщувати січну 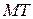 до графіка функції в деякій його точці
до графіка функції в деякій його точці  . Відповідно до побудови кутовий коефіцієнт січної
. Відповідно до побудови кутовий коефіцієнт січної  , (3.25)
, (3.25)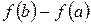 функції на цьому відрізку дорівнює добутку приросту аргументу
функції на цьому відрізку дорівнює добутку приросту аргументу  на значення похідної
на значення похідної  в деякій точці
в деякій точці  , яка знаходиться між точками
, яка знаходиться між точками  і
і  .
. теорему Лагранжа можна записати у вигляді:
теорему Лагранжа можна записати у вигляді: , де
, де 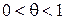 . (3.26)
. (3.26) , то всередині відрізка знайдеться хоча б одна така точка
, то всередині відрізка знайдеться хоча б одна така точка  .
. Рис. 3.6.
Рис. 3.6.
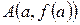 і
і 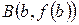 знаходяться на однаковій відстані від вісі
знаходяться на однаковій відстані від вісі  і по один бік від неї (рис. 3.6). Отже, хорда
і по один бік від неї (рис. 3.6). Отже, хорда  . Між цими точками на графіку функції існує хоча б одна точка
. Між цими точками на графіку функції існує хоча б одна точка  , то теорему Ролля можна сформулювати так: між двома коренями функції знаходиться хоча б один корінь похідної, за умови, що функція неперервна на відрізку
, то теорему Ролля можна сформулювати так: між двома коренями функції знаходиться хоча б один корінь похідної, за умови, що функція неперервна на відрізку  існує її похідна.
існує її похідна. неперервні на відрізку
неперервні на відрізку 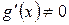
 , то всередині відрізка знайдеться хоча б одна така точка
, то всередині відрізка знайдеться хоча б одна така точка  .
. .
. виконується умова:
виконується умова: 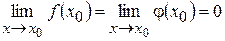 . Тоді відношення
. Тоді відношення 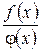 втрачає зміст при
втрачає зміст при  , але границя відношення
, але границя відношення  , неперервні в точці
, неперервні в точці  відрізняється від нуля в точці
відрізняється від нуля в точці  . (3.27)
. (3.27) , для якого виконуються умови теореми. Запишемо відношення
, для якого виконуються умови теореми. Запишемо відношення 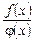 у вигляді
у вигляді 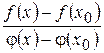 і застосуємо до різниць чисельника і знаменника теорему Лагранжа. Для функції
і застосуємо до різниць чисельника і знаменника теорему Лагранжа. Для функції 
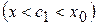 , що
, що  . Для функції
. Для функції 
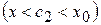 , що
, що  .
. .
.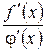 прямує до деякої границі. Оскільки точки
прямує до деякої границі. Оскільки точки  і
і  і
і  , і отже, відношення
, і отже, відношення  прямує до тієї ж границі. Таким чином, при
прямує до тієї ж границі. Таким чином, при  .
. і
і 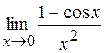 .
.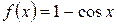 і
і  поблизу точки
поблизу точки  диференційовані, неперервні в точці
диференційовані, неперервні в точці 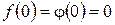 , тому можна застосувати правило Лопіталя.
, тому можна застосувати правило Лопіталя.
 ,
,  ,
, 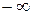 .
. .
. , одержимо, що
, одержимо, що  при
при  і тому, якщо існує границя відношення
і тому, якщо існує границя відношення  при
при  ,
,  поблизу точки
поблизу точки  задовольняють умовам доведеної теореми, тому
задовольняють умовам доведеної теореми, тому ,
, .
. , тобто
, тобто .
. .
. і
і 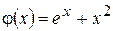 при
при 
 і
і 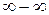 можна привести до розглянутих вище невизначеностей, перетворивши досліджувану функцію на дріб.
можна привести до розглянутих вище невизначеностей, перетворивши досліджувану функцію на дріб. .
.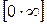 . Перейдемо до дробу, розділивши функцію
. Перейдемо до дробу, розділивши функцію  на функцію
на функцію  , одержимо
, одержимо

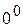 ,
,  ,
,  . Такі невизначеності зустрічаються при обчисленні границі показниково-степеневої функції, тобто функції вигляду
. Такі невизначеності зустрічаються при обчисленні границі показниково-степеневої функції, тобто функції вигляду  .
. . Тоді, якщо
. Тоді, якщо  , то
, то  .
. .
. , тоді
, тоді  і
і  (див. приклад 3.16).
(див. приклад 3.16). .
.


