
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необхідна і достатня умова випуклості (увігнутості) графіка функції.Содержание книги
Поиск на нашем сайте Якщо в усіх точках деякого проміжку друга похідна функції
Доведення проведемо для випадку, коли на проміжку Рівняння кривої має вигляд Оцінимо різницю ординат точок кривої і дотичної для одного й того ж Застосувавши до різниці
де точка Аналогічно можна довести теорему для випадку, якщо друга похідна функції на проміжку додатня. Очевидно, що в точці перегину дотична, якщо вона існує, перетинає криву, оскільки з одного боку від цієї точки крива лежить під дотичною, а з іншого боку – над нею (рис. 3.17, а, б)
Рис. 3.17.
Необхідна умова точки перегину. Якщо точка Необхідна умова просто ілюструється графічно на рис. 3.17, а, б, але не є достатньою. Наприклад, для функції Достатні умови точки перегину. Якщо функція Дійсно, якщо Очевидно, що в точці Можна запропонувати такий алгоритм знаходження проміжків випуклості, увігнутості і точок перегину графіка функції. 1. Знайти область визначення функції. 2. Знайти першу і другу похідні функції. 3. Знайти точки, в яких друга похідна функції дорівнює нулю або не існує. 4. Область визначення знайденими точками розбити на проміжки і дослідити знак другої похідної на кожному з проміжків. Якщо на проміжку Зауважимо, що можна при дослідженні розглядати похідні вищих порядків. Приклад 3.2 2. Знайти проміжки випуклості, увігнутості і точки перегину графіка функції Розв’язання. Відзначимо, що функція визначена на всій числовій прямій. Для неї
Рис. 3.18. Очевидно, що точки з абсцисами
Асимптоти графіка функції Поняття асимптоти вже зустрічалося при вивченні гіперболи. Визначимо асимптоту кривої, заданої рівнянням Означення 3.8. Асимптотою кривої називається пряма (в загальному випадку крива), відстань до якої від точки даної кривої прямує до нуля при необмеженому віддалені цієї точки по кривій від початку координат (рис. 3.19). Будемо розрізняти асимптоти вертикальні, горизонтальні і похилі. Пряма
Рис. 3.19.
Очевидно, що вертикальні асимптоти функція може мати тільки в точках розриву або на границях області визначення. Наприклад, функція Нехай крива Розглянемо різницю ординат графіка функції
Очевидно, якщо
Визначимо з останньої рівності
Якщо
Знаючи
Отже, якщо для функції Якщо Зауважимо, що якщо коефіцієнти Приклад 3.23. Знайти асимптоти графіка функції
Розв’язання. Відзначимо, що задана функція визначена на всій числовій прямій, крім точки
Отже, пряма
Рівняння похилої асимптоти знайдемо у вигляді Згідно з формулами
Отже, пряма
|
||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.15.34 (0.007 с.) |

 від'ємна, то графік функції
від'ємна, то графік функції  на цьому проміжку випуклий; якщо друга похідна додатня, то графік функції
на цьому проміжку випуклий; якщо друга похідна додатня, то графік функції  Рис. 3.16.
Рис. 3.16.
 . Теорема буде доведена, якщо встановимо, що всі точки графіка функції на розглянутому проміжку лежать нижче дотичної, проведеної в деякій точці
. Теорема буде доведена, якщо встановимо, що всі точки графіка функції на розглянутому проміжку лежать нижче дотичної, проведеної в деякій точці 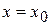 цього проміжку (рис. 3.16).
цього проміжку (рис. 3.16).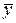 – ордината змінної точки дотичної. Рівняння дотичної до графіка функції в точці
– ордината змінної точки дотичної. Рівняння дотичної до графіка функції в точці  має вигляд
має вигляд 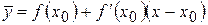 .
. :
: 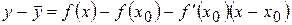 .
.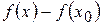 теорему Лагранжа, одержимо
теорему Лагранжа, одержимо 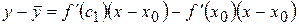 , де точка
, де точка  лежить між точками
лежить між точками 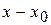 і до виразу в дужках знову застосуємо теорему Лагранжа, одержимо
і до виразу в дужках знову застосуємо теорему Лагранжа, одержимо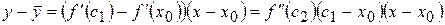 ,
, лежить між
лежить між 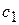 і
і 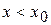 то
то 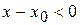 ,
, 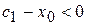 , за умовою
, за умовою 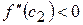 , звідки випливає, що
, звідки випливає, що 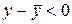 або
або 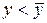 , тобто графік функції розташований під дотичною. Якщо
, тобто графік функції розташований під дотичною. Якщо 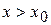 , то
, то 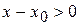 ,
, 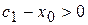 , за умовою
, за умовою 
 дорівнює нулю або не існує.
дорівнює нулю або не існує.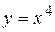 друга похідна
друга похідна 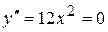 при
при  , але в цій точці графік не має перегину, оскільки крива увігнута на всій числовій вісі.
, але в цій точці графік не має перегину, оскільки крива увігнута на всій числовій вісі.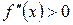 при
при 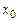 друга похідна функції дорівнює нулю (рис. 3.17, а) або не існує (рис. 3.17, б).
друга похідна функції дорівнює нулю (рис. 3.17, а) або не існує (рис. 3.17, б).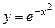 (крива Гауса).
(крива Гауса).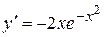 ,
, 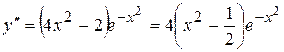 . Друга похідна обертається в нуль, якщо
. Друга похідна обертається в нуль, якщо 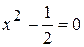 , звідки
, звідки 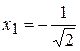 ,
, 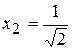 . Зміна знака другої похідної показана на рис. 3.18.
. Зміна знака другої похідної показана на рис. 3.18.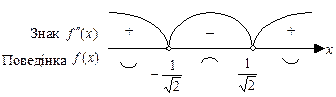
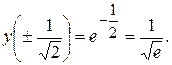
 є вертикальною асимптотою графіка функції
є вертикальною асимптотою графіка функції  .
.
 має вертикальну асимптоту
має вертикальну асимптоту 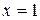 , оскільки
, оскільки  ,
,  . Графік функції зображено на рис. 3. 20.
. Графік функції зображено на рис. 3. 20. . Обчислимо коефіцієнти
. Обчислимо коефіцієнти  і
і  так, щоб відстань
так, щоб відстань  довільної точки
довільної точки  кривої до асимптоти при її віддалені по кривій до нескінченності прямувала до нуля (рис. 3.21).
кривої до асимптоти при її віддалені по кривій до нескінченності прямувала до нуля (рис. 3.21). для одного значення аргументу
для одного значення аргументу  .
. при
при  , то і відстань точки
, то і відстань точки 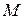 графіка до асимптоти
графіка до асимптоти  . Нехай
. Нехай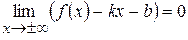 . (3.28)
. (3.28) .
.

 . Оскільки
. Оскільки  , то
, то . (3.29)
. (3.29)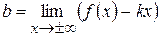 . (3.30)
. (3.30)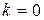 , то рівняння приймає вигляд
, то рівняння приймає вигляд  і асимптота називається горизонтальною.
і асимптота називається горизонтальною.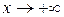 , то асимптота називається правою. Відповідно, якщо
, то асимптота називається правою. Відповідно, якщо 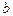 існують і скінченні тільки при
існують і скінченні тільки при 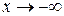 , асимптота називається лівою. При
, асимптота називається лівою. При 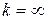 (або
(або 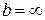 ) графік похилої асимптоти не має.
) графік похилої асимптоти не має.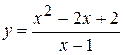 .
. ,
, 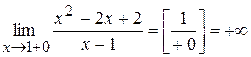 .
.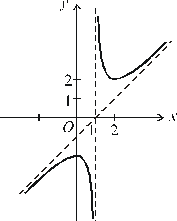 Рис. 3.22.
Рис. 3.22.
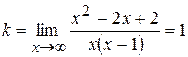 .
.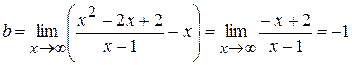
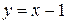 є асимптотою графіка функції (рис. 3.22).
є асимптотою графіка функції (рис. 3.22).


