
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Граничний аналіз в економіці.Содержание книги
Поиск на нашем сайте
В економіці часто використовуються середні величини: середня вартість продукції, середня продуктивність праці і т.п. В однаковій мірі середні величини важливі і при комерційній діяльності: середній доход, середній об'єм продажів і т.п. Але при плануванні розвитку виробництва та будь-якої підприємницької діяльності, виникає, наприклад, така задача: потрібно довідатися, на яку величину виросте результат, якщо будуть збільшені витрати, і, навпаки, наскільки зменшиться результат, якщо витрати скоротяться. Оперуючи середніми величинами, не одержиш відповіді на такі питання. Тут мова йде про прирости змінних величин. У подібних задачах потрібно знайти границю відношення приросту розглянутих величин або, як говорять, граничний ефект. Отже, тут застосовне поняття диференціального числення – похідної функції. Почнемо з поняття граничного прибутку. Загальний чи сумарний прибуток
Крім того, кількість товару (реалізованого) залежить від його ціни. Цей зв'язок дається кривою попиту, яку, будемо вважати лінійною функцією
де кутовий коефіцієнт
Граничний прибуток визначається як похідна від сумарного прибутку
Економічний зміст граничного прибутку дуже простий: він приблизно дорівнює зміні сумарного доходу при зміні кількості реалізованого товару на одиницю. Приблизність викликана тим, що при такому визначенні дотична до графіка заміняється хордою. Ще раз підкреслимо, що прикметник "граничний" в економіці характеризує не самі величини, а ефект їхньої зміни. Крім поняття граничного прибутку, використовується також поняття середнього прибутку,який визначається як прибуток на одиницю продукції
На противагу монополії розглянемо інший граничний випадок – конкурентний ринок. Ця модель припускає, що є велике число незалежних фірм, які продають однорідну продукцію, і немає ніяких перешкод для "входження в ринок". Крім того, кожна фірма робить (продає) лише невелику частку від загального об'єму продукції і не здатна контролювати ціни (змова виключається). При цих умовах можливий стійкий продаж тільки за переважною ринковою ціною. Якщо позначити цю сталу ціну, тобто незалежну від дій окремої фірми, через
граничний прибуток:
середній прибуток:
Звідси випливає, що в моделі чистого ринку граничний і середній прибутки збігаються. Дотепер розглядався прибуток і відповідний йому граничний прибуток, однак такий самий підхід може бути застосований і до інших економічних понять. Наприклад, якщо відома функціональна залежність витрат
Економічний зміст цієї формули такий: граничні витрати приблизно дорівнюють зміні повних витрат при зміні випуску на одиницю. Розглянемо тепер виробничу функцію, тобто таку функцію, незалежна змінна якої приймає значення об’ємів, витраченого або використаного ресурсу (чинника виробництва), а залежна змінна – значення об’ємів продукції, що випускається. Виробнича функція записується у вигляді економіко-математичного рівняння, що зв'язує змінні величини витрат (ресурсів) з величинами продукції (випуску):
Для оцінки ефективності виробництва часто використовується (середня) продуктивність праці
Керівників фірми часто цікавить питання, як зміниться об'єм продукції
Економічний зміст цього поняття очевидний: гранична продуктивність праці приблизно дорівнює зміні об'єму продукції, що випускається, при зміні чисельності персоналу на одиницю. Приклад 3.25. Розглянемо випадок, коли виробнича функція може бути задана емпіричною формулою у вигляді: Розв’язання. Обчислюючи похідну, знаходимо граничну продуктивність праці:
Підставляючи в одержану формулу значення
Звідки видно, що гранична продуктивність праці зменшується з ростом чисельності персоналу і, починаючи з деякої чисельності, стає від'ємною. Це означає, що при подальшому збільшенні персоналу виробництво продукції буде падати. Несподіваний результат! Проте на практиці таке часто спостерігається. Якщо для якоїсь справи залучається занадто багато виконавців, вони починають заважати один одному. Розглянемо ще один приклад граничного аналізу. Розглянемо просту двосекторну макроекономічну модель, у рамках якої національний доход
У свою чергу споживання і заощадження є функціями національного доходу, тобто
Особливий інтерес представляє собою питання: як будуть змінюватися споживання і заощадження при збільшенні (зменшенні) національного доходу. Для аналізу таких проблем вводяться поняття граничної схильності до споживання і граничної схильності до заощадження, що визначаються так:
тобто як похідні за національним доходом Слід зазначити, що у випадку простої двосекторної моделі між граничною схильністю до споживання і граничною схильністю до заощадження існує зв'язок. Дійсно, диференціюючи рівність
одержуємо
Ця формула дозволяє легко обчислювати граничну схильність до споживання, якщо відома гранична схильність до заощадження, і навпаки. Приклад 3.26. Припустимо випадок, що споживання залежить від національного доходу таким чином: Розв’язання. Знаходимо граничну схильність до споживання, оскільки задана саме функція споживання, диференціюючи за
Підставляємо значення національного доходу, що дорівнює 30 одиницям: Звідси можна зробити висновок: при даному рівні національного доходу суспільство більше схильне проїдати його. Дійсно, якщо національний доход збільшується на 1 одиницю від рівня 30, споживання виросте на 0,8 і тільки 0,2 одиниці підуть на інвестиції. Задачі на екстремум. Розглянемо характерний приклади, де для більшої наочності параметрам надано числові значення. Приклад 3.27. Припустимо, що в короткостроковому плані виробнича функція залежить тільки від чисельності персоналу фірми і має вид
де Розв’язання. Насамперед знаходимо стаціонарні точки, для чого обчислюємо похідну і прирівнюємо її до нуля:
Розв’язуючи квадратне рівняння, знаходимо: Обчислюємо другу похідну:
При Для другої точки:
Встановимо деякі загальні співвідношення, властиві виробничій функції. Раніше відзначалося, що в простих випадках виробнича функція пов'язує випуск продукції
Там же було введене поняття середньої продуктивності праці
Цікаво з'ясувати, при якому значенні Для цього знайдемо стаціонарні точки, використовуючи правило диференціювання відношення двох функцій
Згадуючи, що за означенням гранична продуктивність праці Приклад 3.28. Залежність річних витрат управління запасами від розміру партії замовлення має вигляд:
де Визначити економічний розмір замовлення Розв’язання. Маємо Визначимо економічний розмір замовлення, якщо Тоді Приклад 3.29. Відомо, що крива попиту має вигляд Розв’язання. Прибуток можна отримати як різницю між доходом та витратами, а доход – як ціну помножену на кількість:
Функцію прибутку дослідимо на екстремум:
Вправи 3.1. Знайти похідні функцій за означенням: а) г) ж) 3.2. Знайти похідну функції 3.3.–3.41. Знайти похідні функцій. 3.3. 3.5. 3.7. 3.9. 3.11. 3.13. 3.15. 3.17. 3.19. 3.21. 3.23. 3.24. 3.25. 3.26. 3.27. 3.28. а) в) 3.29. а) 3.30. 3.32. 3.34. 3.36. 3.38. 3.39. 3.40. 3.41. а) г) ж) 3.42.–3.43. Знайти похідну параметрично заданої функції. 3.42. а) 3.43. а) 3.44. Знайти похідні другого порядку для функцій: а) 3.45. Для функції 3.46. Знайти диференціали функцій для довільних аргументу і приросту: а) 3.47. Обчислити приблизно: а) д) 3.48. Знайти похідну вказаного порядку: а) в) д) ж) і) 3.49. Знайти диференціал указаного порядку: а) 3.50. Довести тотожності: а) б) 3.51. Довести нерівності: а) в) д) 3.52–3.66. Обчислити границі, використовуючи правила Лопіталя. 3.52. 3.54. 3.56. 3.58. 3.60. 3.62. 3.64. 3.66. 3.67.–3.70. Знайти інтервали монотонності і екстремуми функції. 3.67. 3.69. 3.71. Знайти найменше і найбільше значення функції на проміжку: а) 3.72. Потрібно виготовити шухляду з кришкою, об'єм якої дорівнює 72 см3, причому сторони основи повинні відноситись як 1:2. Які повинні бути розміри всіх сторін, щоб повна поверхня була найменшою? 3.73. Через дану точку 3.74–3.76. Знайти проміжки випуклості, вгнутості і точки перегину графіка функції. 3.74. 3.76. 3.77–3.79. Знайти асимптоти графіків функцій. 3.77. 3.80.–3.82. Дослідити функції і побудувати їхні графіки: 3.80. а) в) 3.81. а) в) д) 3.82. а) 3.83. а) 3.84. Лісівники знайшли, що твірна стовбура європейської сосни досить добре описується рівнянням
де Дослідити функцію 3.85. Написати розклад по цілим невід’ємним степеням змінної а) в) д) 3.86. Використовуючи формулу Тейлора, обчислити границі: а) в) 3.87. Залежність між витратами виробництва 3.88. Нехай вартість 3.89. Розрахувати еластичність даних функцій та знайти значення показника еластичності для заданих а) б) в) г) д) є) 3.90. Крива повних витрат 1) 2) 3) 4) 5) 6) 7) 3.91. Функції попиту а) б) в) г) Знайти ціну рівноваги, еластичність попиту і пропозиції для цієї ціни, зміну прибутку у відсотках при збільшенні ціни на 3% від рівноваги. 3.92. Для наступних функцій попиту знайти таке значення а) в) 3.93. Дана функція а) б) в) 3.94. Обсяг продукції 3.95. Нехай функція витрат і прибуток при виробництві а) б) Чистий прибуток: 3.96. Визначити оптимальне для виробника значення випуску а) б) в) г) д) є) 3.97. Функція витрат має вигляд: 3.98. Відомо, що прогнозована ціна акції має вигляд: | ||||||||||||||
|
| Поделиться: |

 природно визначити як добуток ціни одиниці товару
природно визначити як добуток ціни одиниці товару  на кількість товару
на кількість товару 
 .
. ,
, від'ємний, а параметр
від'ємний, а параметр  додатній, тому функція
додатній, тому функція 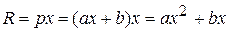 .
. .
. .
. ,
, ,
, .
. від об'єму продукції
від об'єму продукції  , можна визначити граничні витрати так:
, можна визначити граничні витрати так: .
. (
( ,
,  ). У загальному випадку виробництво продукції (продукція розуміється широко і вміщує в себе, наприклад, комерційну і фінансову діяльність) залежить від багатьох чинників. Така залежність однієї величини від ряду інших є функцією декількох змінних і буде розглядатися в наступному розділі. Зараз же обмежимося випадком, коли кількість продукції
). У загальному випадку виробництво продукції (продукція розуміється широко і вміщує в себе, наприклад, комерційну і фінансову діяльність) залежить від багатьох чинників. Така залежність однієї величини від ряду інших є функцією декількох змінних і буде розглядатися в наступному розділі. Зараз же обмежимося випадком, коли кількість продукції  (для фірми це просто чисельність персоналу). У короткостроковому плані таке допущення може бути і виробничу функцію можна записати так:
(для фірми це просто чисельність персоналу). У короткостроковому плані таке допущення може бути і виробничу функцію можна записати так: .
. :
: .
. .
. . Розрахувати граничну продуктивність праці.
. Розрахувати граничну продуктивність праці. .
.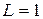 ;
; 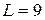 ;
;  ;
;  ;
; 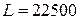 . Результати обчислень представлені у вигляді таблиці:
. Результати обчислень представлені у вигляді таблиці:
 представляє суму споживання
представляє суму споживання 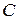 і заощаджень
і заощаджень 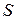 (заощадження звичайно втілюються в капіталовкладеннях чи інвестиціях):
(заощадження звичайно втілюються в капіталовкладеннях чи інвестиціях):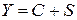 .
. ,
,  .
. ;
;  ,
, .
. . Потрібно знайти граничні схильності до споживання і заощадження, коли національний доход складає 30 одиниць (
. Потрібно знайти граничні схильності до споживання і заощадження, коли національний доход складає 30 одиниць (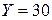 ).
).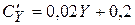 .
. . Тепер знаходимо граничну схильність до заощадження:
. Тепер знаходимо граничну схильність до заощадження: 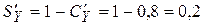 .
. ,
, .
. ,
, 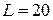 .
. .
.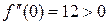 . Таким чином, в цій точці є мінімум. Це природно: важко очікувати випуску якоїсь продукції, якщо немає жодного працюючого.
. Таким чином, в цій точці є мінімум. Це природно: важко очікувати випуску якоїсь продукції, якщо немає жодного працюючого. . Тому в цій точці є максимум. Відповідний випуск продукції
. Тому в цій точці є максимум. Відповідний випуск продукції .
.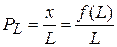 .
. .
. , умову стаціонарності можна переписати у вигляді:
, умову стаціонарності можна переписати у вигляді:  . Звідки остаточно маємо
. Звідки остаточно маємо 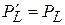 , тобто в стаціонарних точках гранична продуктивність праці дорівнює середньої продуктивності праці.
, тобто в стаціонарних точках гранична продуктивність праці дорівнює середньої продуктивності праці. ,
, – розмір замовленої партії;
– розмір замовленої партії;  – витрати виконання замовлення;
– витрати виконання замовлення;  – закупівельна ціна одиниці товару;
– закупівельна ціна одиниці товару; 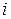 – витрати зберігання, що виражаються як доля від закупівельної ціни одиниці товару.
– витрати зберігання, що виражаються як доля від закупівельної ціни одиниці товару. ,
,  ,
,  – формула Уілсона,
– формула Уілсона,  ,
,  , тоді
, тоді  – точка мінімуму.
– точка мінімуму. грош. од.,
грош. од., 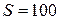 од.,
од.,  грош. од.,
грош. од.,  .
. (од.) – оптимальне замовлення.
(од.) – оптимальне замовлення. , (
, ( ,
,  ), де
), де  , де
, де 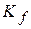 – сталі витрати;
– сталі витрати; 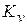 – питомі змінні витрати. Визначити, при якому обсязі виробництва
– питомі змінні витрати. Визначити, при якому обсязі виробництва 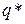 прибуток буде найбільший.
прибуток буде найбільший. ,
, , звідки
, звідки  ,
,  , (оскільки
, (оскільки  ), тобто
), тобто 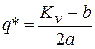 – точка максимуму.
– точка максимуму.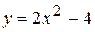 ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; є)
; є)  ;
; ; з)
; з) 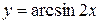 ; і)
; і) 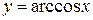 .
.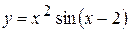 у точці
у точці  .
. . 3.4.
. 3.4.  .
. . 3.6.
. 3.6. 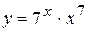 .
. . 3.8.
. 3.8.  .
.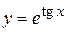 . 3.10.
. 3.10. 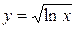 .
. . 3.12.
. 3.12.  .
. . 3.14.
. 3.14.  .
. . 3.16.
. 3.16.  .
. . 3.18.
. 3.18. 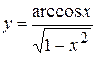 .
. . 3.20.
. 3.20.  .
. . 3.22.
. 3.22.  .
. .
.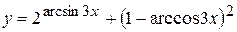 .
. .
. .
. .
. ; б)
; б)  ;
; .
. ; б)
; б)  ; в)
; в)  .
. . 3.31.
. 3.31.  .
.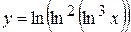 . 3.33.
. 3.33. 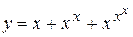 .
. . 3.35.
. 3.35.  .
.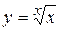 . 3.37.
. 3.37.  .
. .
. .
. .
.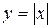 ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; є)
; є)  ;
; .
. б)
б) 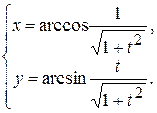
 б)
б) 
 ; б)
; б) 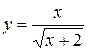 .
. обчислити приріст функції і диференціал при
обчислити приріст функції і диференціал при 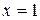 ,
,  .
. ; б)
; б)  ; в)
; в)  .
.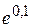 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; ; є)
; є) 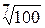 ; ж)
; ж)  ; з)
; з)  .
. ,
,  ,
,  ; б)
; б)  ,
,  ;
; ,
,  ,
,  ;
; ,
,  ; є)
; є)  ,
,  ,
,  ,
,  ,
, 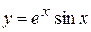 ,
, 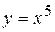 ,
,  ; б)
; б) 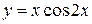 ,
,  ; в)
; в)  ,
, 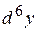 .
.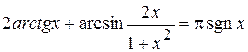 ,
,  ;
;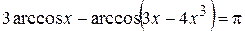 ,
,  .
. ,
,  ; б)
; б)  ,
,  ;
;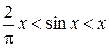 ,
,  ; г)
; г) 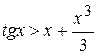 ,
, 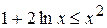 ,
,  . 3.53.
. 3.53.  .
. . 3.55.
. 3.55.  .
. . 3.57.
. 3.57. 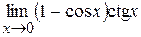 .
. . 3.59.
. 3.59. 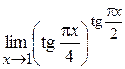 .
. . 3.61.
. 3.61.  .
. . 3.63.
. 3.63.  .
.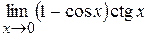 . 3.65.
. 3.65.  .
. .
. . 3.68.
. 3.68.  .
.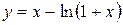 . 3.70.
. 3.70.  .
. ,
, 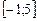 ; б)
; б)  ,
, 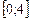 .
. провести пряму так, щоб сума довжин додатних відрізків, що відтинаються нею на координатних осях, була найменшою.
провести пряму так, щоб сума довжин додатних відрізків, що відтинаються нею на координатних осях, була найменшою.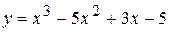 . 3.75.
. 3.75.  .
. .
.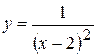 . 3.78.
. 3.78. 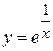 . 3.79.
. 3.79.  .
.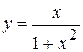 ; б)
; б)  ;
; ; г)
; г)  .
.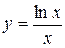 ;
; ; г)
; г) 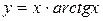 ;
; ; є)
; є)  .
. . б)
. б) 
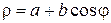 ; б)
; б)  .
. ,
, ,
, 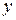 – радіус поперечного переріза стовбура,
– радіус поперечного переріза стовбура, 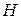 – висота стовбура,
– висота стовбура,  і переконатися, що її властивості відповідають наочним уявленням про деревний стовбур (функція спадає, спочатку увігнута, потім опукла). Побудувати схематичний графік функції.
і переконатися, що її властивості відповідають наочним уявленням про деревний стовбур (функція спадає, спочатку увігнута, потім опукла). Побудувати схематичний графік функції. до
до  ; б)
; б)  до
до  ;
; до
до 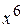 ; г)
; г)  до
до  ;
; до
до  ; б)
; б)  ;
; .
. і обсягом продукції
і обсягом продукції  (грош. од.). Визначити середні і граничні витрати, якщо обсяг продукції 10 од., 20 од., 100 од.
(грош. од.). Визначити середні і граничні витрати, якщо обсяг продукції 10 од., 20 од., 100 од. . Яка маргінальна вартість при
. Яка маргінальна вартість при 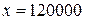 ?
? ,
,  ;
;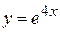 ,
,  ,
,  ,
, 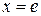 ,
,  ;
; ,
, 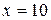 ,
,  ;
; ,
, 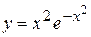 ,
,  .
. . Визначити: а) криву граничних витрат; б) розрахувати коефіцієнти еластичності при заданих значеннях
. Визначити: а) криву граничних витрат; б) розрахувати коефіцієнти еластичності при заданих значеннях  ,
,  ;
; ,
,  ,
,  ;
; ,
,  ,
,  ;
; ,
, 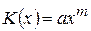 ,
,  ;
; ,
,  ,
, 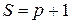 ;
; ,
,  ;
; ,
,  ;
;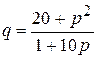 ,
,  .
. ; б)
; б) 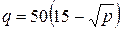 ;
; .
. повних витрат виробництва. Знайти обсяг виробництва, при якому середні витрати будуть мінімальні.
повних витрат виробництва. Знайти обсяг виробництва, при якому середні витрати будуть мінімальні.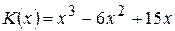 ;
;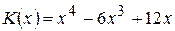 ;
; .
.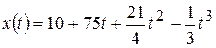 ,
,  , де
, де  – робочий день у годинах. Знайти: а) продуктивність праці, швидкість і темп її зміни; б) при якому значенні
– робочий день у годинах. Знайти: а) продуктивність праці, швидкість і темп її зміни; б) при якому значенні  ,
, 
 ,
,  ,
,  .
. .Визначити оптимальне для виробника значення випуску
.Визначити оптимальне для виробника значення випуску  .
. ,
,  ;
; ,
, 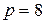 ;
; ,
,  ;
; ,
,  ;
;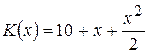 ,
,  ;
; ,
,  .
. . На початковому етапі фірма організує виробництво таким чином, щоб мінімізувати середні витрати
. На початковому етапі фірма організує виробництво таким чином, щоб мінімізувати середні витрати  . В подальшому на товар встановлюється ціна 4 грош. од. за одиницю. На скільки одиниць товару фірмі потрібно збільшити випуск?
. В подальшому на товар встановлюється ціна 4 грош. од. за одиницю. На скільки одиниць товару фірмі потрібно збільшити випуск? , де
, де  – початкова ціна,
– початкова ціна,  – відносний прибуток корпорації,
– відносний прибуток корпорації,  –частка прибутку на виплату дивідендів,
–частка прибутку на виплату дивідендів,  – найбільш ефективна ставка, по якій можливо реінвестувати дивіденди. розглядаються дві акції з початковою ціною 1 грош. од. і характеристиками:
– найбільш ефективна ставка, по якій можливо реінвестувати дивіденди. розглядаються дві акції з початковою ціною 1 грош. од. і характеристиками:  ,
, 


