
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зростання і спадання функції на проміжкуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Як відомо, функція Аналогічно, функція називається спадною на даному проміжку, якщо для будь-яких точок З цих означень випливає, що функція зростає на проміжку, якщо для будь-яких двох точок Необхідна умова зростання і спадання функції. Якщо диференційована функція Дійсно, нехай, наприклад, функція Аналогічно доводиться необхідна умова спадання функції на проміжку. Геометрично тлумачення теореми означає, що в кожній точці графіка зростаючої функції дотична утворює гострий кут з віссю Достатня умова зростання і спадання функції. Нехай Нехай, наприклад, на даному проміжку
де точка Оскільки Аналогічно розглядається випадок, коли На рис. 3.7 інтервали монотонності розділені точками
Рис. 3.7.
Виходячи зі сказаного, можна сформулювати такий порядок дослідження функції на монотонність: - знайти область визначення функції; - знайти похідну функції; - знайти критичні точки. - критичними точками область визначення функції розбити на проміжки і досліджувати знак Говорять, якщо на проміжку Приклад 3.18. Знайти інтервали монотонності функції Розв’язання. Функція визначена на всій числовій прямій, крім точки Схематично результат дослідження зображено на рис. 3.8.
Рис. 3.8.
Екстремуми функції Нехай функція Означення 3.5. Точка Точки максимуму і мінімуму функції називають точками екстремуму. Значення функції Функція
Рис. 3.9.
На рис. 3.10 зображена функція, у якої в точці
|
|||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 774; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.158.124 (0.008 с.) |

 називається зростаючою на даному проміжку, якщо для будь-яких двох точок
називається зростаючою на даному проміжку, якщо для будь-яких двох точок  ,
,  цього проміжку з умови
цього проміжку з умови  випливає
випливає 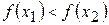 , тобто меншому значенню аргументу відповідає менше значення функції.
, тобто меншому значенню аргументу відповідає менше значення функції.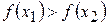 , тобто меншому значенню аргументу відповідає більше значення функції.
, тобто меншому значенню аргументу відповідає більше значення функції. і
і  приріст аргументу
приріст аргументу  і приріст функції
і приріст функції  одного знака на цьому проміжку, і відповідно функція спадає на проміжку, якщо для неї на цьому проміжку приріст аргументу і приріст функції різних знаків.
одного знака на цьому проміжку, і відповідно функція спадає на проміжку, якщо для неї на цьому проміжку приріст аргументу і приріст функції різних знаків. цього проміжку
цього проміжку  . Якщо диференційована функція
. Якщо диференційована функція  .
. одного знака з
одного знака з  . Переходячи в цій нерівності до границі при
. Переходячи в цій нерівності до границі при  , одержуємо
, одержуємо  .
. , а в кожній точці графіка спадної функції дотична утворює тупий кут з віссю
, а в кожній точці графіка спадної функції дотична утворює тупий кут з віссю  ,
, лежить між точками
лежить між точками  , то знаки різниць
, то знаки різниць  і
і  однакові, тобто функція на даному проміжку зростає.
однакові, тобто функція на даному проміжку зростає. ,
,  , причому в точці
, причому в точці 
 на кожному з проміжків.
на кожному з проміжків. , то це проміжок зростання, якщо ж
, то це проміжок зростання, якщо ж  , то це проміжок спадання.
, то це проміжок спадання.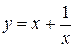 .
. , тобто її область визначення складається з інтервалів
, тобто її область визначення складається з інтервалів  . Похідна функції
. Похідна функції  дорівнює нулю при
дорівнює нулю при  , тобто
, тобто  . Розв’язуючи рівняння, одержимо дві стаціонарні точки
. Розв’язуючи рівняння, одержимо дві стаціонарні точки 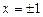 . Похідна не існує при
. Похідна не існує при  ,
,  ,
,  , що розбивають область визначення функції на проміжки
, що розбивають область визначення функції на проміжки  ,
,  ,
,  ,
,  . Знак похідної на кожному проміжку визначимо за значенням похідної в деякій, довільно обраній точці проміжку. Наприклад, знак похідної на проміжку
. Знак похідної на кожному проміжку визначимо за значенням похідної в деякій, довільно обраній точці проміжку. Наприклад, знак похідної на проміжку  :
:  , отже на цьому проміжку функція зростає. Провівши аналогічні дослідження, одержимо, що на проміжках
, отже на цьому проміжку функція зростає. Провівши аналогічні дослідження, одержимо, що на проміжках 
 .
. з цього околу виконується нерівність
з цього околу виконується нерівність 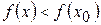 (рис. 3.9, а). Точка
(рис. 3.9, а). Точка 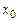 називається точкою мінімуму функції
називається точкою мінімуму функції 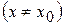 цього околу виконується нерівність
цього околу виконується нерівність  (рис. 3.9, б).
(рис. 3.9, б).
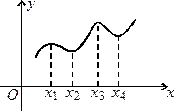 Рис. 3.10.
Рис. 3.10.
 . Але це не суперечить означенню екстремуму функції, оскільки в означенні екстремуму порівнюються значення функції в точці і деякому її околі. Говорять, що мова йде про локальні екстремуми.
. Але це не суперечить означенню екстремуму функції, оскільки в означенні екстремуму порівнюються значення функції в точці і деякому її околі. Говорять, що мова йде про локальні екстремуми.


