
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівняння дотичної площини і нормалі до поверхні. Екстремум функції двох зміннихСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рівняння дотичної площини і нормалі до поверхні
Нехай функція Необхідна умова існування екстремуму. Якщо диференційована функція
Точки, в яких виконуються рівності (2.11), називаються точками можливого екстремуму або стаціонарними. Достатня умова існування екстремуму функції. Нехай у точці а) якщо б) якщо в) у випадку
Зразки розв’язування задач 1. Скласти рівняння дотичної площини і нормалі до поверхні а) Знайдемо Позначимо
Обчислимо значення частинних похідних в точці
Згідно з формулою (2.9), рівняння дотичної площини має вигляд:
За формулою (2.10) складемо рівняння нормалі:
б) Знайдемо Значення частинних похідних в точці
Складемо рівняння дотичної площини:
Рівняння нормалі:
2. Дослідити функції на екстремум: а) Обчислимо частинні похідні функції: Знайдемо стаціонарні точки. Для цього розв’яжемо систему рівнянь:
Визначаючи друге, маємо: Отже, точки Знайдемо їх значення в стаціонарних точках:
Враховуємо, що екстремуму немає. Обчислимо б) Частинні похідні першого порядку: стаціонарні точки:
Отже, точка
Тоді
Отже, в точці
Завдання для самостійної роботи 1. Скласти рівняння дотичної площини і нормалі до поверхні у заданій точці: а) б) в) 2. Дослідити функції на екстремум: а)
Розділ 3 НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ Поняття первісної функції та невизначеного інтеграла. Метод безпосереднього інтегрування Функція Сукупність усіх первісних функції
де Операцію знаходження невизначеного інтеграла від функції називають інтегруванням цієї функції. Властивості невизначеного інтеграла: 1. 2. 3. 4. 5. 6. Якщо При обчисленні невизначених інтегралів зручно користуватися наступними правилами: якщо
де
Таблиця основних інтегралів 1.
1'.
2.
3.
3'.
4.
5.
6.
7.
8.
8'.
9.
9'.
10.
11.
12.
13.
14.
15. Зауваження. Варто відзначити, що задача інтегрування функції вирішується неоднозначно. Тобто один і той же інтеграл може бути обчислений не єдиним методом. Метод безпосереднього інтегрування полягає у зображенні вихідного інтеграла у вигляді алгебраїчної суми табличних інтегралів.
Зразки розв’язування задач Обчислити інтеграли. 1.
Користуючись властивостями 4 та 5, будемо мати:
2.
3.
4.
5. Тут, крім властивостей 4 та 5, застосуємо правила інтегрування. Дістанемо:
6.
7.
Інтеграл не є табличним, тому за допомогою алгебраїчних перетворень треба підінтегральну функцію подати у такому вигляді, щоб можна було застосувати властивості невизначеного інтеграла та обчислити його. Для цього в чисельнику дробу додамо і віднімемо 1. Поділивши почленно
8. Використаємо формулу тригонометрії:
Тоді
Завдання для самостійної роботи Обчислити інтеграли:
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
|
||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 660; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.172 (0.011 с.) |

 в даній її точці
в даній її точці  мають вигляд:
мають вигляд: ; (2.9)
; (2.9) . (2.10)
. (2.10)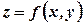 визначена в деякому околі точки
визначена в деякому околі точки  . Точка
. Точка  називається точкою максимуму (мінімуму) функції
називається точкою максимуму (мінімуму) функції  , якщо знайдеться такій окіл точки
, якщо знайдеться такій окіл точки 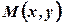 виконується нерівність:
виконується нерівність: 
 . Максимуми і мінімуми функції називаються її екстремумами, а точки, в яких досягаються екстремуми - точками екстремуму.
. Максимуми і мінімуми функції називаються її екстремумами, а точки, в яких досягаються екстремуми - точками екстремуму. ,
,  . (2.11)
. (2.11) і покладемо
і покладемо  . Тоді:
. Тоді: , то
, то  - точка максимуму, при
- точка максимуму, при  - мінімуму;
- мінімуму; , то в точці
, то в точці  , функція
, функція  у стаціонарній точці
у стаціонарній точці  :
: у точці
у точці  .
. :
:  . Отже,
. Отже,  .
. .Тоді частинні похідні:
.Тоді частинні похідні: ,
,  ,
,  .
. ,
, ,
, .
. ,
, або
або  .
. .
. у точці
у точці  .
. ,
,  ,
,  .
. ,
, ,
, .
. ,
, або
або  .
. або
або  .
. .
. ,
, 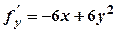 .
. або
або 
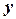 з першого рівняння і підставляючи його вираз
з першого рівняння і підставляючи його вираз  у
у , звідки
, звідки  ,
,  . Тоді
. Тоді  ,
,  .
. і
і  - стаціонарні. Обчислимо частинні похідні другого порядку даної функції:
- стаціонарні. Обчислимо частинні похідні другого порядку даної функції:  ,
,  ,
,  .
. ,
,  ,
,  ;
; ,
, 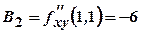 ,
,  .
. , отже, в точці
, отже, в точці  та
та  , а тому в точці
, а тому в точці  .
. .
. та
та  . Знайдемо
. Знайдемо

 , звідки
, звідки 
 є стаціонарною. Частинні похідні другого порядку:
є стаціонарною. Частинні похідні другого порядку: ,
,  ,
,  .
. ,
,  ,
,  . Обчислимо
. Обчислимо  .
.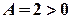 , то в точці
, то в точці  .
. ,
,  ;
; ,
,  ,
,  .
. ; б)
; б)  .
. називається первісною функції
називається первісною функції  на проміжку
на проміжку  , якщо
, якщо  для всіх
для всіх  . Очевидно, що будь-яка з функцій
. Очевидно, що будь-яка з функцій  , де
, де  - довільна стала, також є первісною функції
- довільна стала, також є первісною функції  ,
, - підінтегральний вираз,
- підінтегральний вираз,  .
. .
. .
. .
. .
. і
і  - довільна функція, що має неперервну похідну, то
- довільна функція, що має неперервну похідну, то  .
. ,
, ,
, ,
, та
та 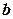 - сталі величини.
- сталі величини.
 ,
, ,
,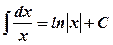 ,
, ,
,  >
>  ,
,  ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,  ,
, ,
, 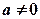 ,
, ,
,  ,
, ,
, ,
, ,
, .
. .
.






 .
.
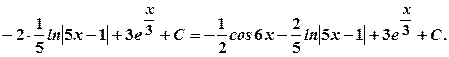



 .
. на
на  , отримаємо алгебраїчну суму двох табличних інтегралів:
, отримаємо алгебраїчну суму двох табличних інтегралів:
 .
. .
.
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.


