
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Канонічні рівняння ліній другого порядку.Содержание книги
Поиск на нашем сайте Рівняння кола з центром
Рівняння еліпса: Рівняння гіперболи: Рівняння параболи симетричної відносно осі Рівняння параболи симетричної відносно осі Вступ в математичний аналіз Якщо кожному значенні змінної Множина Х називається областю визначення функції, множина Множина значень Числа Число Якщо послідовність має скінчену границю, то її називають збіжною. Важливим прикладом числової послідовності є геометрична прогресія. Послідовність чисел називається геометричною прогресією, якщо кожний наступний її член дорівнює попередньому помноженому на деяке стале число Число Основні теореми про границі функцій: 1. Границя сталої дорівнює цій сталій. 2. Границя алгебраїчної суми, добутку, частки двох функцій дорівнює відповідно алгебраїчній сумі, добутку та частці їх границь при умові, що границя функції в знаменнику не дорівнює 0. Випадки, коли не можна знайти границі безпосередньо за цими теоремами, це невизначеності: 1. 2. В фінансових розрахунках використовують формули нагромадження капіталу за складними відсотками знайдені на основі геометричної прогресії: Якщо відсотки нараховуються Якщо зростання за складними відсотками неперервне, то на основі другої визначної границі формула набуде вигляду Диференціальне числення функцій однієї змінної Похідною функції у=f(x) в точці x називається границя відношення приросту функції ∆ у до приросту аргументу ∆х в цій точці, коли ∆х →0 Позначають похідну
Якщо ця границя скінченна, то функція називається диференційованою в т.
Диференціал функції
Застосування похідної. Правило Лопіталя. Для “невизначеностей типу Достатні умови зростання та спадання функції. Якщо похідна неперервної на відрізку Необхідні умови екстремуму функції. Якщо в точці Точки, в яких похідна дорівнює нулю або не існує називають критичними. Достатні умови екстремуму (перше правило). Якщо при переході через критичну точку Друге правило. Якщо в критичній точці Графік функції Точка В економічних дослідженнях використовують поняття еластичності функції
Повне дослідження функції Загальна схема дослідження функції і побудова її графіка. 1. Знаходимо область визначення функції у = f(x). 2. Знаходимо точки перетину кривої у=f(x) з осями координат, відкладаємо їх на рисунку. 3. Визначаємо, чи симетрична крива у = f(x) відносно осей координат і початку координат (парність і непарність). 4. Досліджуємо функцію на неперервність. Якщо функція маєу точці x 0 розрив, то визначаємо, якого він роду. 5. Досліджуємо функцію на періодичність. 6. Знаходимо асимптоти кривої, якщо вони існують. 7. Визначаємо інтервали монотонності, максимум і мінімум функції і позначаємо на рисунку точки кривої з максимальною і мінімальною ординатами. 8. Знаходимо точки перегину, інтервали опуклості і увігнутості. Функції багатьох змінних Якщо кожній парі чисел Змінні Якщо Частинні похідні першого порядку:
Їх знаходять як звичайні похідні, вважаючи при обчисленні Необхідні умови екстремуму функції двох змінних Якщо в точці
Достатні умови екстремуму функції двох змінних Нехай в точці Визначимо: Якщо Якщо Градієнтом функції двох змінних називається вектор g = Для функції g = Невизначений інтеграл. Первісною функцією до заданої функції
Множина всіх первісних Отже, В формулі
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.147 (0.01 с.) |

 і радіусом
і радіусом 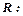

 , де
, де  і
і  - півосі еліпса,
- півосі еліпса,  відстань від центра до одного з фокусів,
відстань від центра до одного з фокусів,  - ексцентриситет еліпса.
- ексцентриситет еліпса.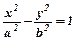 , де
, де  - відстань від центра до одного з фокусів,
- відстань від центра до одного з фокусів,  - асимптоти гіперболи.
- асимптоти гіперболи.
 її фокус
її фокус  , директриса:
, директриса: 

 , її фокус
, її фокус 
 директриса:
директриса: 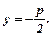
 поставлено у відповідність за певним правилом значення
поставлено у відповідність за певним правилом значення  то говорять, що задана функція. Її позначають
то говорять, що задана функція. Її позначають 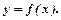
 - областю значень функції.
- областю значень функції. яка за певним правилом поставлена у відповідність натуральному ряду чисел
яка за певним правилом поставлена у відповідність натуральному ряду чисел 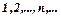 називається числовою послідовністю.
називається числовою послідовністю. називають членами послідовності, при цьому
називають членами послідовності, при цьому  - загальним членом.
- загальним членом. , якщо для всякого як завгодно малого додатнього числа
, якщо для всякого як завгодно малого додатнього числа  знайдеться такий номер
знайдеться такий номер 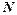 , що для всіх
, що для всіх 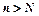 виконується нерівність
виконується нерівність  . Це позначають
. Це позначають 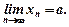
 - знаменник прогресії:
- знаменник прогресії: 
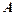 називається границею функції
називається границею функції  в точці
в точці  , якщо для будь-якої збіжної до
, якщо для будь-якої збіжної до  відповідна послідовність значень функції
відповідна послідовність значень функції  збіжна до
збіжна до 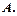 Це записують
Це записують 
 Для розкриття невизначеностей використовують визначні границі:
Для розкриття невизначеностей використовують визначні границі:
 .
. де
де  - сума вкладу нагромадження через
- сума вкладу нагромадження через 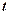 років,
років,  - початкова сума вкладу,
- початкова сума вкладу, 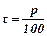 - коефіцієнт складних відсотків при
- коефіцієнт складних відсотків при  - щорічному відсотковому приросту.
- щорічному відсотковому приросту. разів за рік, то
разів за рік, то 

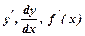 .
. .
.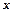 . Основні правила і формули диференціювання поміщені в таблиці:
. Основні правила і формули диференціювання поміщені в таблиці: v
v
 v'
v'


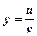


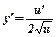
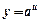

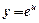





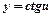














 обчислюється за формулою:
обчислюється за формулою: .
. та
та  ” границя відношення функцій дорівнює границі відношення їх похідних, якщо вона існує.
” границя відношення функцій дорівнює границі відношення їх похідних, якщо вона існує.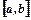 функції
функції  в цій точці дорівнює нулю або не існує.
в цій точці дорівнює нулю або не існує. , то в цій точці функція
, то в цій точці функція  має екстремум: максимум при
має екстремум: максимум при 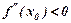 , мінімум при
, мінімум при  .
. , якщо в кожній точці його
, якщо в кожній точці його  і при переході через яку
і при переході через яку 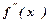 змінює знак є точкою перегину.
змінює знак є точкою перегину. .
. , де
, де  ,
,  поставлено у відповідність за певним правилом значення
поставлено у відповідність за певним правилом значення  , то говорять, що задана функція двох змінних, яку позначають
, то говорять, що задана функція двох змінних, яку позначають  .
.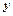 називають аргументами.
називають аргументами. , а
, а  одержить приріст
одержить приріст 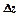 . Частинний приріст
. Частинний приріст  , частинний приріст
, частинний приріст  .
. ,
,  .
. змінну
змінну  змінну
змінну 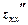 ,
,  ,
,  .
.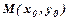 функція
функція 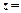
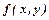 досягає екстремуму, то її частинні похідні перешого порядку в цій точці дорівнюють нулю:
досягає екстремуму, то її частинні похідні перешого порядку в цій точці дорівнюють нулю:
 виконується умова
виконується умова  і існують частинні похідні другого порядку
і існують частинні похідні другого порядку 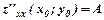 ;
; 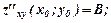
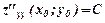 .
.
 то в точці
то в точці  то екстремуму немає.
то екстремуму немає. і
і  (або
(або  ), то функція досягає мінімуму, якщо
), то функція досягає мінімуму, якщо  (або
(або  ), то функція досягає максимуму.
), то функція досягає максимуму. .
. 
 градієнт має вид
градієнт має вид

 , похідна якої дорівнює
, похідна якої дорівнює  :
: або
або  .
.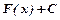 для даної функції
для даної функції  - довільна стала, називається невизначеним інтегралом від функції
- довільна стала, називається невизначеним інтегралом від функції  .
. .
. - знаком невизначеного інтеграла.
- знаком невизначеного інтеграла.


