
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференціальні рівняння першого порядку.Содержание книги
Поиск на нашем сайте
Диференціальним рівнянням першого порядку називається рівняннявигляду Функція Задача знаходження розв’язку, який задовільняє початкові умови Розглянемо деякі класи диференціальних рівнянь, які розв’язуються в квадратурах (розв’язки виражаються через інтеграли від заданих функцій). Диференціальне рівняння вигляду Диференціальне рівняння вигляду В ньому змінні можна розділити і знайти загальний інтеграл
Зауваження. Часто для зручності спрощень Лінійним дифрінянням першого порядку називається рівняння, яке містить шукану функцію Підстановкою Однорідним дифрівнянням першого порядку називається рівняння вигляду Однорідне дифрівняння зводиться до рівняння вигляду Підстановкою
Лінійні диференціальні рівняння другого Порядку з постійними коефіцієнтами. Лінійним диференціальним рівнянням другого порядку з постійними коефіцієнтами називається рівняння вигляду Відповідним характеристичним рівнянням називається рівняння:
Загальний розв’язок заданого дифрівняння залежить від коренів цього характеристичного рівняння. 1. Якщо корені характеристичного рівняння дійсні та різні, 2. Якщо корені характеристичного рівняння дійсні і рівні, тобто 3. Якщо корені характеристичного рівняння комплексно спряжені, тобто Неоднорідне лінійне дифрівняння другого порядку з постійними коефіцієнтами має вигляд Загальний розв’язок лінійного дифрівняння ( Частковий розв’язок ( 1. Нехай
2. Нехай
Для дифрівняння другого порядку загальний розв’язок містить дві довільні сталі. Задача Коші ставиться так: Знайти такий розв’язок, який би задовільняє умови Числові ряди
Нехай задана нескінченна послідовність чисел Вираз Частковою сумою числового ряду називають суму Сумою Якщо границя часткової суми ряду є скінченним числом, то ряд називають збіжним і позначають Якщо границя часткової суми ряду не існує або дорівнює Числовий ряд вигляду При Числовий ряд вигляду Необхідна ознака збіжності числового ряду. Якщо числовий ряд Достатні ознаки збіжності числових рядів. 1. Ознака Даламбера. Нехай усі члени числового ряду
Якщо 2. Ознака порівняння. Нехай треба дослідити збіжність заданого ряду: а) якщо б) якщо 3. Інтегральна ознака Коші. Нехай Тоді для збіжності ряду необхідно і достатньо, щоб невласний інтеграл Якщо члени числового ряду мають різні знаки, то ряд називають знакозмінним. Ряд, члени якого почергово мають додатний та від’ємний знаки, називають знакопереміжним. Такий ряд можна записати у вигляді:
Ознака Лейбніца. Якщо абсолютні величини знакопереміжного ряду монотонно спадають Якщо знакопереміжний ряд збігається, а ряд, складений з абсолютних величин, розбігається, то знакопереміжний ряд називають неабсолютно збіжним (або умовно збіжним). Степеневі ряди. Степеневим рядом називають ряд такого вигляду:
де Число Радіус збіжності знаходимо за формулою: Інтервал Ряд Тейлора: Ряд Маклорена:
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

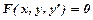 , яке, коли його можна розв’язати відносно
, яке, коли його можна розв’язати відносно 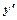 набуває вигляду
набуває вигляду 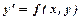 або
або 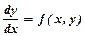 .
.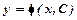 , де
, де  - довільна стала, називається загальним розв’язком рівняння першого порорядку, якщо при підстановці її в рівняння, вона перетворює його в правильну рівність. Якщо цей розв’язок задає функцію
- довільна стала, називається загальним розв’язком рівняння першого порорядку, якщо при підстановці її в рівняння, вона перетворює його в правильну рівність. Якщо цей розв’язок задає функцію 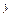 неявно:
неявно: 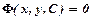 , то знайдено загальний інтеграл. При довільному
, то знайдено загальний інтеграл. При довільному 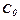 одержимо частковий розв’язок (частковий інтеграл).
одержимо частковий розв’язок (частковий інтеграл).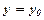 при
при 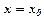 , називається задачею Коші для рівняння першого порядку.
, називається задачею Коші для рівняння першого порядку.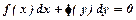 називається рівнянням з відокремленими змінними. Його загальний інтеграл:
називається рівнянням з відокремленими змінними. Його загальний інтеграл: 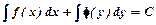 .
.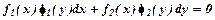 називається рівнянням з відокремлюваними змінними.
називається рівнянням з відокремлюваними змінними.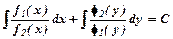 .
.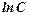 .
.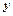 , та її похідну
, та її похідну 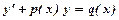 .
.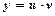 , за методом Бернулі воно приводиться до інтегрування двох дифрівнянь з відокремлюваними змінними.
, за методом Бернулі воно приводиться до інтегрування двох дифрівнянь з відокремлюваними змінними.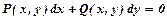 , де
, де 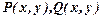 - однорідні функції одного виміру. Функція
- однорідні функції одного виміру. Функція 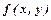 називається однорідною виміру
називається однорідною виміру  , якщо
, якщо 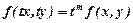 .
.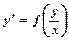 .
.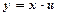 воно зводиться до рівняння з відокремлюваними змінними.
воно зводиться до рівняння з відокремлюваними змінними.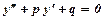 , де
, де 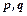 - сталі числа.
- сталі числа.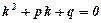 .
.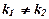 , то загальний розв’язок дифрівняння має вигляд
, то загальний розв’язок дифрівняння має вигляд 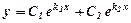 .
.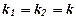 , то загальний розв’язок
, то загальний розв’язок 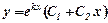 .
.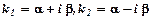 ,де
,де 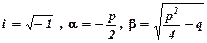 , то загальний розв’язок
, то загальний розв’язок 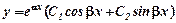 .
.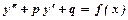 , де
, де 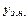 ) дорівнює сумі загального розв’язку відповідного однорідного рівняння (
) дорівнює сумі загального розв’язку відповідного однорідного рівняння (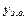 ) і довільного часткового розв’язку (
) і довільного часткового розв’язку (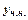 ) даного неоднорідного рівняння, тобто
) даного неоднорідного рівняння, тобто 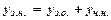
 подібним до неї.
подібним до неї.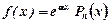 , де многочлен
, де многочлен 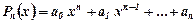 . Тоді частковий розв’язок шукаємо у вигляді
. Тоді частковий розв’язок шукаємо у вигляді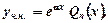 якщо
якщо 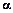 - не корінь характеристичного рівняння;
- не корінь характеристичного рівняння;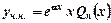 , якщо
, якщо 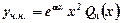 , якщо
, якщо 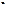
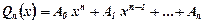 ,(
,(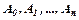 -невідомі сталі коефіцієнти, які знаходяться методом невизначених коефіцієнтів).
-невідомі сталі коефіцієнти, які знаходяться методом невизначених коефіцієнтів).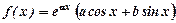 , тоді частковий розв’язок
, тоді частковий розв’язок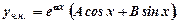 якщо
якщо 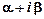 - не корінь характеристичного рівняння;
- не корінь характеристичного рівняння;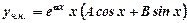 , якщо
, якщо 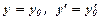 , при
, при 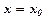 .
.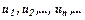
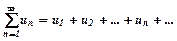 називають нескінченним числовим рядом (або просто рядом), числа
називають нескінченним числовим рядом (або просто рядом), числа 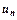 – загальним членом ряду.
– загальним членом ряду.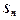 перших
перших 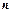 членів числового ряду, тобто
членів числового ряду, тобто 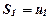 ,
, 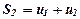 ,...,
,..., 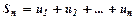 .
.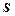 числового ряду
числового ряду 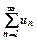 називають границю його часткової суми
називають границю його часткової суми 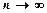 , тобто
, тобто 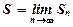 .
.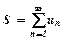 .
.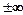 , то числовий ряд називають розбіжним.
, то числовий ряд називають розбіжним.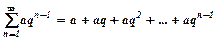 називають рядом геометричної прогресії зі знаменником
називають рядом геометричної прогресії зі знаменником  .
.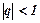 ряд геометричної прогресії збігається і його сума дорівнює
ряд геометричної прогресії збігається і його сума дорівнює 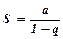 . При
. При 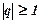 ряд розбігається.
ряд розбігається.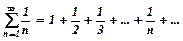 називають гармонічним рядом. Цей ряд розбігається.
називають гармонічним рядом. Цей ряд розбігається.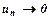 при
при 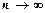 , тобто
, тобто 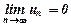 .
.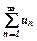 додатні і при необмеженому зростанні номера
додатні і при необмеженому зростанні номера 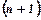 -го члена до
-го члена до 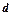 . Тобто
. Тобто 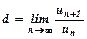 .
.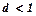 , тоді числовий ряд збігається. При
, тоді числовий ряд збігається. При 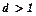 , цей ряд розбігається. При
, цей ряд розбігається. При 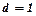 потрібно застосовувати іншу ознаку.
потрібно застосовувати іншу ознаку.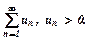 Візьмемо другий додатний числовий ряд, збіжність чи розбіжність якого відома:
Візьмемо другий додатний числовий ряд, збіжність чи розбіжність якого відома: 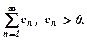 Тоді:
Тоді: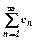 ряд збігається і, починаючи з деякого номера
ряд збігається і, починаючи з деякого номера 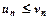 , тоді й ряд
, тоді й ряд 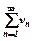 ряд розбігається і, починаючи з деякого номера
ряд розбігається і, починаючи з деякого номера 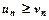 , тоді й ряд
, тоді й ряд 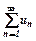 також розбігається.
також розбігається.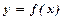 -неперервна, монотонно спадна і додатна в інтервалі
-неперервна, монотонно спадна і додатна в інтервалі 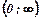 функція, значення якої
функція, значення якої 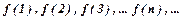 дорівнюють відповідним додатним членам ряду
дорівнюють відповідним додатним членам ряду 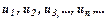
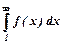 мав скінченну величину.
мав скінченну величину.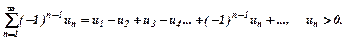 Знакопереміжний ряд називають збіжним абсолютно, якщо збігається додатний числовий ряд
Знакопереміжний ряд називають збіжним абсолютно, якщо збігається додатний числовий ряд 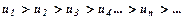 і границя загального члена дорівнює нулю при
і границя загального члена дорівнює нулю при 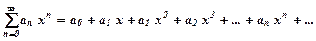 або
або 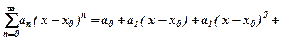
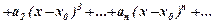 ,
,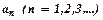 - дійсні числа, які називають коефіцієнтами степеневого ряду;
- дійсні числа, які називають коефіцієнтами степеневого ряду; 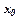 -деяке постійне число.
-деяке постійне число.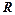 називають радіусом збіжності степеневого ряду, якщо для
називають радіусом збіжності степеневого ряду, якщо для 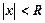 ряд збігається, а для
ряд збігається, а для 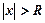 - розбігається.
- розбігається.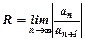 .
.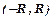 називають інтервалом збіжності степеневого ряду.
називають інтервалом збіжності степеневого ряду.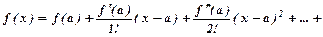
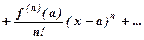 .
.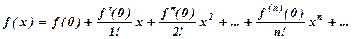 .
.


