
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Означення та область визначення. Частинні похідні першого порядкуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Нехай Змінну Множину пар чисел Оскільки кожній упорядкованій парі чисел Значення функції Величина Величина Якщо існує границя
Якщо існує границя
При обчисленні частинних похідних функції двох змінних користуються вже відомими формулами і правилами диференціювання функції однієї змінної. Слід лише пам’ятати, що при знаходженні частинної похідної Зразки розв’язування задач 1. Знайти та зобразити області визначення функцій двох змінних: а) Функція не визначена лише тоді, коли б) Функція визначена при умові
в)
г) z Областю визначення цієї функції є сукупність пар
2. Знайти частинні похідні функцій: а) Функція
б) Вважаючи, що Якщо, в)
г)
д) При диференціюванні по
При диференціюванні по
є) Аналогічно попередньому прикладу маємо:
ж) При знаходженні частинних похідних
з) При диференціюванні по і) Аналогічно попередньому прикладу маємо: по к) Обчислюючи Обчислюючи похідну л)
м)
н)
3. Довести, що функція Знайдемо частинні похідні функції
Підставимо саму функцію
Будемо мати:
Отримано тотожність, це означає, що функція
Завдання для самостійної роботи 1. Знайти область визначення функцій: а) 2. Знайти частинні похідні функцій: а) б) в) г) д) є) ж) з)
3. Довести, що функція
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 779; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

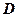 - множина упорядкованих пар чисел
- множина упорядкованих пар чисел  . Якщо кожній парі чисел
. Якщо кожній парі чисел 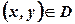 за певним законом відповідає число
за певним законом відповідає число 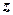 , то кажуть, що на множині
, то кажуть, що на множині 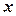 і
і 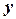 і записують
і записують 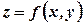 .
.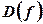 . Множину значень
. Множину значень 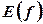 .
.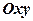 єдина точка
єдина точка 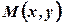 площини, і, навпаки, кожній точці
площини, і, навпаки, кожній точці  і замість
і замість  . Областю визначення функції у цьому випадку є деяка множина точок площини
. Областю визначення функції у цьому випадку є деяка множина точок площини 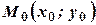 позначають
позначають 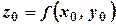 або
або 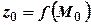 , або
, або 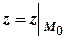 .
. називається частинним приростом функції
називається частинним приростом функції 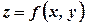 по змінній
по змінній  називається частинним приростом функції
називається частинним приростом функції 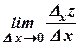 , то вона називається частинною похідною функції
, то вона називається частинною похідною функції 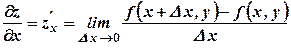 .
.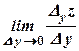 , то вона називається частинною похідною функції
, то вона називається частинною похідною функції  .
. обчислюють звичайну похідну функції змінної
обчислюють звичайну похідну функції змінної 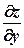 сталою вважається змінна
сталою вважається змінна 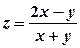 .
.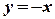 . Геометрично це означає, що область визначення функції складається із двох півплощин, одна з яких лежить вище, а друга нижче прямої
. Геометрично це означає, що область визначення функції складається із двох півплощин, одна з яких лежить вище, а друга нижче прямої 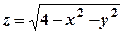 .
. , тобто
, тобто 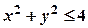 . Рівняння
. Рівняння  визначає в площині
визначає в площині 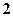 . Функція визначена в точках, які лежать усередині кола та на його межі, так як для всіх точок, які лежать поза колом, має місце нерівність
. Функція визначена в точках, які лежать усередині кола та на його межі, так як для всіх точок, які лежать поза колом, має місце нерівність  (рис.2.2).
(рис.2.2).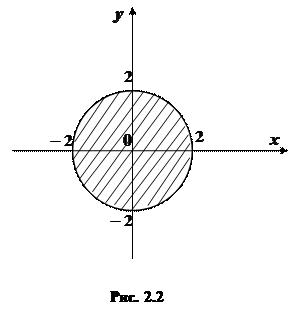
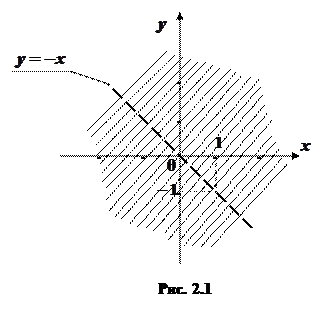
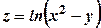 .
. Область визначення цієї функції визначається з нерівності
Область визначення цієї функції визначається з нерівності 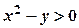 . Межа області – парабола
. Межа області – парабола  , яка ділить всю площину на дві частини. Щоб виявити, яка з частин є областю визначення даної функції, тобто задовольняє умову
, яка ділить всю площину на дві частини. Щоб виявити, яка з частин є областю визначення даної функції, тобто задовольняє умову 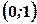 належить області визначення, тому що
належить області визначення, тому що 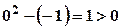 . Отже, область визначення даної функції є множина точок, розташованих нижче параболи. Межа (парабола
. Отже, область визначення даної функції є множина точок, розташованих нижче параболи. Межа (парабола 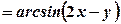 .
.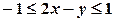 . На площині
. На площині 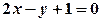 і
і  (рис.2.4)
(рис.2.4)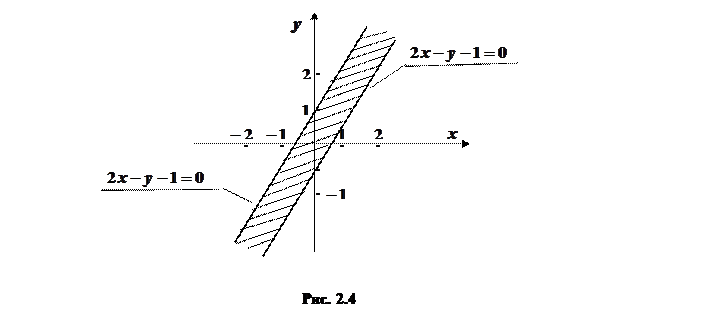
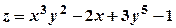 .
. . Припускаючи, що стала
. Припускаючи, що стала 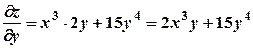 .
. .
.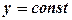 , маємо:
, маємо: 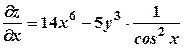 .
.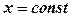 , то
, то 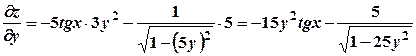 .
.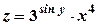 .
. ;
; 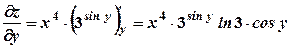 .
.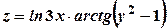 .
.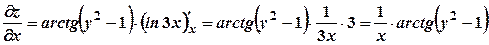 ;
;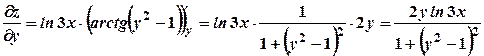 .
.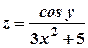 .
.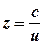 . Тому
. Тому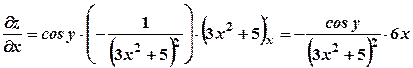 .
.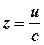 , тому
, тому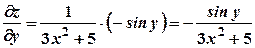 .
. .
.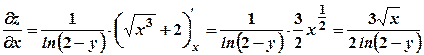 ;
;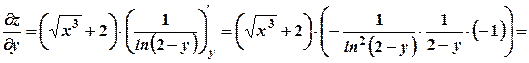
 .
.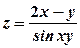 .
. ;
;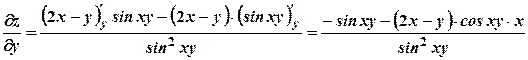 .
. .
.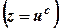 . Тоді отримаємо
. Тоді отримаємо  . При диференціюванні по
. При диференціюванні по 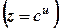 . Будемо мати
. Будемо мати  .
. .
.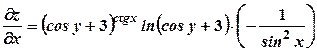 ;
; 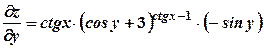 .
.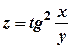 .
. і знаходимо частинну похідну від складеної функції по
і знаходимо частинну похідну від складеної функції по 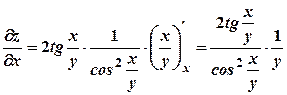 .
. .
.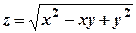 .
.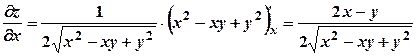 ;
;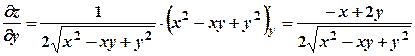 .
.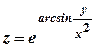 .
.
 ;
; 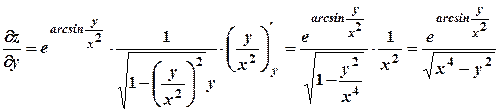 .
. .
.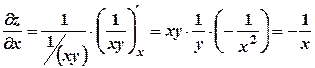 ;
;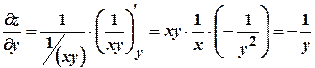 .
.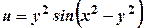 задовольняє рівняння
задовольняє рівняння 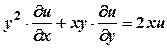 .
. :
: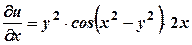 ;
;  .
.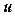 та її частинні похідні в наведене рівняння:
та її частинні похідні в наведене рівняння: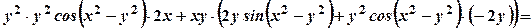
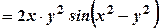 .
.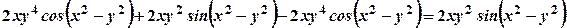 ;
;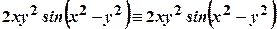 .
. ; б)
; б)  ; в)
; в)  ; г)
; г) 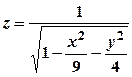 .
.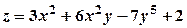 ;
;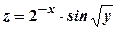 ;
; ;
;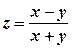 ;
;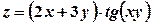 ;
;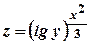 ;
; ;
;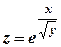 .
.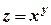 задовольняє рівняння
задовольняє рівняння 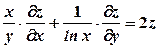 .
.


