
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтегрування функцій, раціонально залежнихСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Від тригонометричних Домовимось позначати 1) Інтеграли виду
При цьому використовуються формули:
Варто помітити, що недоліком цієї підстановки є той факт, що її використання в багатьох випадках зводить вихідний інтеграл до інтегралу від раціонального дробу з великими степенями. Тому в багатьох випадках користуються іншими підстановками. Наведемо деякі з них: а) б) Використовується підстановка в)
г) 2) Інтеграли виду а) якщо б) якщо в) якщо
г) якщо д) якщо
3) Інтеграли виду
Зразки розв’язування задач Обчислити інтеграли. Почнемо з прикладів ілюструючих різні випадки пункту 1. 1. Застосуємо до інтеграла універсальну підстановку Тоді
2.
3.
4. Зауважимо на те, що підінтегральна функція непарна відносно Отримаємо:
5. Підінтегральна функція непарна відносно Отже,
Зауваження: отриманий інтеграл
6. Так як підінтегральна функція є раціональною функцією від
7. В цьому випадку зручнішою буде підстановка
8. Підінтегральна функція є раціональною функцією відносно
Порівнюючи коефіцієнти при однакових степенях
9. Підінтегральна функція непарна відносно Після розкладання дробу
Коефіцієнти розкладання
Далі розглянемо приклади різних випадків пункту 2.
10.
При заміні Тут доцільна підстановка
11.
12. Підінтегральна функція містить тільки парний степінь синуса, який допускає пониження степеня за формулою:
13.
Застосуємо заміну
14. Показники
15. Показники
Перейдемо до розглядання прикладів до пункту 3. 16. Перетворимо добуток тригонометричних функцій в суму згідно з наведеною формулою:
17.
Завдання для самостійної роботи Обчислити інтеграли: 1. 2. 3. 4. 5.
6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16.
Насамперед зауважимо, що інтеграл від іраціональної функції не завжди обчислюється в скінченному вигляді. Розглянемо деякі типи таких інтегралів, які за допомогою певної підстановки можна звести до інтеграла від раціональної функції, а отже, знайти його. 1) Інтеграли виду
2) Інтеграли виду де 3) а) Інтеграли виду
б) інтеграли виду 4) Для перелічених нижче видів іраціональностей використовуються тригонометричні підстановки, що дозволяють прийти до інтегралів від тригонометричних функцій Розглянемо випадки: а) для інтегралів виду б) для інтегралів виду в) для інтегралів виду
Зразки розв’язування задач Обчислити інтеграли.
1. Найменшим спільним кратним показників коренів є
Отримали інтеграл від неправильного раціонального дробу. Виділивши цілу частину дробу і виконавши почленне ділення в отриманому правильному дробу, матимемо:
Повернемось до початкової змінної, враховуючи що 2. Для інтегрування отриманого раціонального дробу запишемо його у вигляді суми найпростіших дробів:
Невизначені коефіцієнти Шуканий інтеграл матиме вигляд:
3.
4.
5.
6.
7. Введемо підстановку Після підстановки отримаємо:
Повернувшись до початкової змінної, маємо:
8. Виділимо під коренем повний квадрат, звівши тим самим інтеграл до табличного:
9. Перетворимо підкореневий вираз:
Тоді інтеграл має вигляд:
10. Використаємо підстановку
Внесемо в знаменнику
11. Обчислимо даний інтеграл за допомогою заміни Маємо: Обчислимо отриманий інтеграл, використовуючи формулу пониження степеня: Отримаємо:
Зауваження. У перетвореннях використовуються тотожності:
12.
Враховуючи, що
13.
Зауваження. У перетвореннях використовуються тотожності:
Завдання для самостійної роботи Обчислити інтеграли: 1. 2. 3. 4. 5. 6. Л І Т Е Р А Т У Р А 1. Дубовик В.П., Юрик І.І. Вища математика: Навч. посібник. – К.: А.С.К., 2001. 2. Овчинников П.П. та ін. Вища математика: Підручник. У 2 ч. – К.: Техніка, 2004. 3. Шипачёв В.С. Высшая математика: Учебник для вузов. – М.: Высшая школа, 1998. 4. Шкіль М.І., Колесник Т.В. Вища математика. У 3-х кн.. – К: Либідь, 1994. 5. Вища математика: Збірник задач: Навч. посібник / За ред. В.П. Дубовика, І.І. Юрика. – К.: А.С.К., 2004. 6. Шипачёв В.С. Задачник по высшей математике: Учебное пособие для вузов.- М.: Высшая школа, 2002. 7. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч.: Учебное пособие для вузов. – М.: Высшая школа, 2000.
Навчальне видання
Кадильникова Тетяна Михайлівна Шинковська Iрина Леонідівна Заєць Iрина Петрівна
Запорожченко Олена Євгенівна Бас Тетяна Петрівна
ВИЩА МАТЕМАТИКА В ПРИКЛАДАХ ТА ЗАДАЧАХ Частина II Навчальний посібник
Тем. план 2010, поз.250
Підписано до друку 27.10.2010. Формат 60x84 1/16 Папір друк. Друк плоский. Облік.-вид.арк. 5,30. Умов. друк. арк.5,22. Тираж 100 пр. Замовлення №.
Національна металургійна академія України 49600, м. Дніпропетровськ – 5, пр. Гагаріна, 4 ____________________________________________ Редакційно-видавничий відділ НМетАУ
|
|||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.85.61 (0.008 с.) |

 - раціональну функцію, залежну від
- раціональну функцію, залежну від  , якщо вона утворена з цих тригонометричних функцій та сталих за допомогою раціональних алгебраїчних дій.
, якщо вона утворена з цих тригонометричних функцій та сталих за допомогою раціональних алгебраїчних дій. приводяться до інтегралів від раціональної функції нового аргументу
приводяться до інтегралів від раціональної функції нового аргументу  підстановкою
підстановкою , яка називається універсальною.
, яка називається універсальною. ,
,  ,
,  ,
,  .
. , тобто підінтегральна функція непарна відносно
, тобто підінтегральна функція непарна відносно  . Використовується підстановка
. Використовується підстановка  , тоді
, тоді 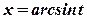 ,
,  ;
;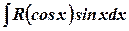 - підінтегральна функція непарна відносно
- підінтегральна функція непарна відносно  .
. , тоді
, тоді  ,
,  ;
; . При цьому використовуються формули:
. При цьому використовуються формули: ,
,  ,
, 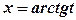 ,
, 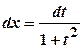 ;
; . Тут підінтегральна функція залежить раціональним образом тільки від
. Тут підінтегральна функція залежить раціональним образом тільки від  . Слід застосовувати підстановку
. Слід застосовувати підстановку  обчислюються за допомогою таких підстановок:
обчислюються за допомогою таких підстановок: - ціле додатне непарне число:
- ціле додатне непарне число:  ;
; - ціле додатне непарне число:
- ціле додатне непарне число:  ,
,  ;
; ,
,  ,
,  обчислюються за допомогою тригонометричних формул:
обчислюються за допомогою тригонометричних формул: ,
, ,
, .
. .
.
 .
.

 .
.

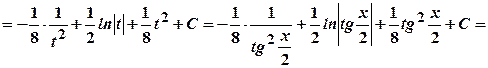
 .
.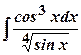 .
. один множник, а
один множник, а  виразимо через
виразимо через  . Інтеграл матиме вигляд:
. Інтеграл матиме вигляд: 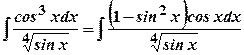 , тобто ми звели його до випадку
, тобто ми звели його до випадку  .
.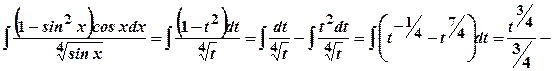
 .
. .
. .
.
 .
. може бути обчислений іншим методом за допомогою формул тригонометрії, а саме:
може бути обчислений іншим методом за допомогою формул тригонометрії, а саме: .
. .
. та
та 

 .
.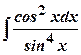 .
.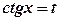 ,
,  . Перетворивши підінтегральний вираз та використавши наведену підстановку, отримаємо:
. Перетворивши підінтегральний вираз та використавши наведену підстановку, отримаємо: .
.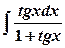 .
. . Останній інтеграл є інтегралом від правильного раціонального дробу. Для інтегрування розкладемо дріб на суму найпростіших:
. Останній інтеграл є інтегралом від правильного раціонального дробу. Для інтегрування розкладемо дріб на суму найпростіших: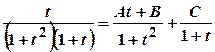 ,
,  .
.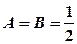 ,
,  . Отже,
. Отже,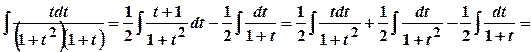
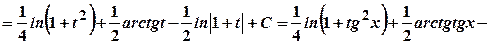
 .
. .
. ;
;  ,
,  .
. на суму найпростіших одержимо:
на суму найпростіших одержимо: .
. обчислюються звичними методами і дорівнюють:
обчислюються звичними методами і дорівнюють:  ,
, 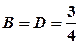 ,
,  . Тоді інтеграл дорівнюватиме:
. Тоді інтеграл дорівнюватиме: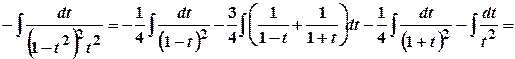
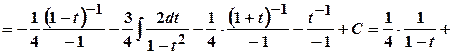


 .
. (тут
(тут  - ціле додатне непарне).
- ціле додатне непарне). на
на  підінтегральна функція не змінює знак.
підінтегральна функція не змінює знак.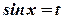 ,
,  ,
,  .
.
 .
. (
(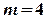 ,
, 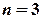 - ціле додатне непарне число).
- ціле додатне непарне число).
 .
. .
. . Отже,
. Отже, 
 .
.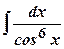 (
( ,
,  - ціле парне від’ємне число).
- ціле парне від’ємне число). .
. ,
, 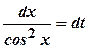 ,
,  . Тоді
. Тоді 
 .
. .
. обидва парні від’ємні. Зручною буде заміна
обидва парні від’ємні. Зручною буде заміна  ,
,  ,
, 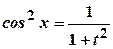 . Після підстановки інтеграл набуває вигляду:
. Після підстановки інтеграл набуває вигляду:

 .
. .
.

 .
.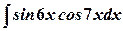 .
. . Проінтегруємо отриманий вираз:
. Проінтегруємо отриманий вираз: .
.
 .
. ;
;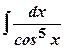 ;
; ;
; ;
; ;
; ;
;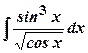 ;
; ;
; ;
;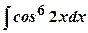 ;
; ;
; ;
; ;
; ;
; ;
; .
. 3.6. Інтегрування деяких іраціональних функцій
3.6. Інтегрування деяких іраціональних функцій , де
, де  >
>  ,
,  - натуральні числа, обчислюються за допомогою підстановки
- натуральні числа, обчислюються за допомогою підстановки  , де
, де  - спільний знаменник дробів
- спільний знаменник дробів 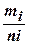 .
. ,
, - дійсні числа, причому
- дійсні числа, причому  (бо у противному випадку відношення
(бо у противному випадку відношення  є сталим і підінтегральна функція в цьому разі є раціональною функцією від
є сталим і підінтегральна функція в цьому разі є раціональною функцією від  ) за допомогою підстановки
) за допомогою підстановки  зводяться до інтегралів від раціональної функції змінної
зводяться до інтегралів від раціональної функції змінної  вилученням повного квадрату під радикалом зводяться до табличних інтегралів:
вилученням повного квадрату під радикалом зводяться до табличних інтегралів: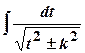 ,
,  ;
; за допомогою підстановки
за допомогою підстановки  зводяться до інтегралів попереднього виду.
зводяться до інтегралів попереднього виду. застосовується підстановка
застосовується підстановка 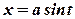 або
або 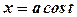 ;
; застосовується підстановка
застосовується підстановка  або
або  ;
; підстановка
підстановка  або
або  дає змогу позбутися іраціональності.
дає змогу позбутися іраціональності. .
. . Виконаємо підстановку
. Виконаємо підстановку  ,
,  ,
, 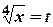 ,
,  .
. .
.
 .
. . Тоді
. Тоді  .
. .
. .
.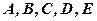 знайдемо порівнянням коефіцієнтів при однакових степенях
знайдемо порівнянням коефіцієнтів при однакових степенях  .Отримаємо:
.Отримаємо:  .
.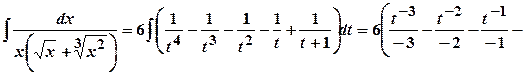

 .
.
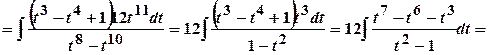

 .
.
 .
.
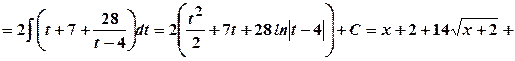
 .
.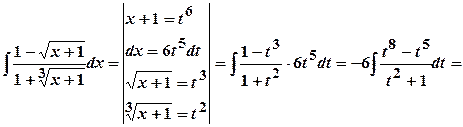
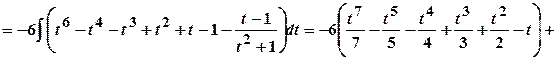

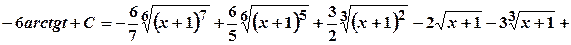
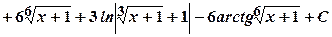 .
.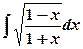 .
. . Тоді
. Тоді  ,
, 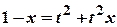 ,
,  ,
,  , звідки
, звідки  . Знайдемо
. Знайдемо  :
: 
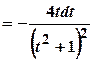 .
. . Інтеграл може бути обчислений розкладанням дробу на суму найпростіших дробів. Розглянемо інший спосіб. Проінтегруємо частинами:
. Інтеграл може бути обчислений розкладанням дробу на суму найпростіших дробів. Розглянемо інший спосіб. Проінтегруємо частинами:
 .
.

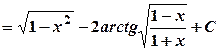 .
. .
.
 .
. .
.
 .
.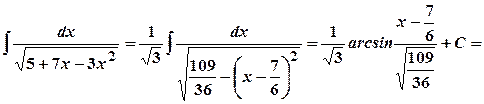
 .
. .
.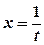 ,
, 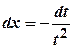 .
.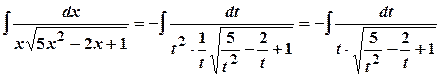 .
.
 .
. .
. . Тоді
. Тоді  ,
, 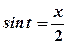 ,
,  .
.
 .
. .
.
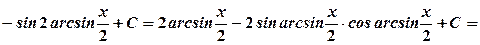

 .
.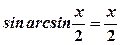 ,
,  .
.
 .
. , маємо далі:
, маємо далі:

 .
.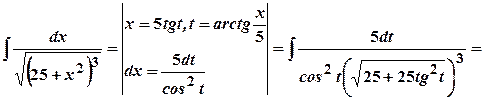



 .
. ,
,  .
. ;
; ;
; ;
; ;
; ;
; .
.


