
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтегрування раціональних дробів, тригонометричних та ірраціональних функцій.Содержание книги
Поиск на нашем сайте
До раціональних функцій належать цілі та дробові раціональні функції. Інтегрування цілих раціональних функцій (многочленів) не складне. Розглянемо дробово-раціональну функцію (раціональний дріб), яка являє собою відношення двох многочленів степенів
Раціональний дріб називають правильним, якщо степінь чисельника менше від степеня знаменника Якщо раціональний дріб (3.1) неправильний, то діленням многочлена
де многочлен Отже, щоб проінтегрувати правильний раціональний дріб 1) розкласти многочлен 2) розкласти дріб
де Для їх знаходження найчастіше користуються так званим методом невизначених коефіцієнтів. Потрібно звести праву частину рівності (3.2)до спільного знаменника, який дорівнює многочлену
Існує ще один спосіб знаходження невизначених коефіцієнтів. У рівності тотожніх многочленів чисельників лівого та правого дробу розкладання (3.2)слід надавати змінній 3) тепер залишається обчислити I. II. III. IV. де
Зразки розв’язування задач Обчислити інтеграли. 1. Дріб
Отже, розкладання раціонального дробу на найпростіші має вигляд:
Невідомі
При В результаті отримали ті самі значення Таким чином,
Зауваження. Якщо корені знаменника – числа тільки дійсні та різні, спосіб часткових значень є найзручнішим. В інших випадках поєднують обидва способи.
Інтегрування функцій, раціонально залежних Від тригонометричних Домовимось позначати 1) Інтеграли виду
При цьому використовуються формули:
Варто помітити, що недоліком цієї підстановки є той факт, що її використання в багатьох випадках зводить вихідний інтеграл до інтегралу від раціонального дробу з великими степенями. Тому в багатьох випадках користуються іншими підстановками. Наведемо деякі з них: а) б) Використовується підстановка в)
г) 2) Інтеграли виду а) якщо б) якщо в) якщо
г) якщо д) якщо
3) Інтеграли виду
Зразки розв’язування задач Обчислити інтеграли. Почнемо з прикладів ілюструючих різні випадки пункту 1. 1. Застосуємо до інтеграла універсальну підстановку Тоді
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.195.90 (0.009 с.) |

 і
і 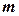 із коефіцієнтами
із коефіцієнтами  та
та  відповідно:
відповідно: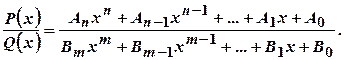 (3.1)
(3.1) <
<  . У противному разі, а саме при
. У противному разі, а саме при  , дріб називають неправильним.
, дріб називають неправильним. на
на  його можна подати у вигляді суми цілої раціональної функції та правильного раціонального дробу, тобто
його можна подати у вигляді суми цілої раціональної функції та правильного раціонального дробу, тобто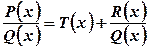 ,
, - частка від ділення, многочлен
- частка від ділення, многочлен  - остача від ділення.
- остача від ділення. , треба:
, треба: , де
, де  - дійсні числа,
- дійсні числа,  - цілі додатні числа,
- цілі додатні числа,  -
-  не має дійсних коренів
не має дійсних коренів  <
<  ;
; (3.2)
(3.2) ,
, - невизначені коефіцієнти (деякі дійсні числа).
- невизначені коефіцієнти (деякі дійсні числа). лівої та правої частин тотожності, дістанемо систему лінійних алгебраїчних рівнянь, з якої визначаються шукані невідомі
лівої та правої частин тотожності, дістанемо систему лінійних алгебраїчних рівнянь, з якої визначаються шукані невідомі 
 ,…,
,…, .
. ;
; як суму інтегралів від знайдених елементарних дробів. При цьому матимемо справу із наступними інтегралами:
як суму інтегралів від знайдених елементарних дробів. При цьому матимемо справу із наступними інтегралами: ,
, 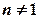 .
. ,
,  .
. ,
,  .
. ,
, ,
, 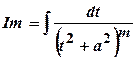 , в якому
, в якому  , визначається
, визначається  - кратним застосуванням рекурентної формули
- кратним застосуванням рекурентної формули .
. .
. є правильним. Розкладемо його на суму найпростіших дробів. Коренями знаменника є дійсні числа
є правильним. Розкладемо його на суму найпростіших дробів. Коренями знаменника є дійсні числа  та
та  , серед яких немає кратних. Тому чисельниками кожного дробу будуть числа
, серед яких немає кратних. Тому чисельниками кожного дробу будуть числа  . Отримаємо:
. Отримаємо:  . Помноживши обидві частини рівності на спільний знаменник, здобудемо:
. Помноживши обидві частини рівності на спільний знаменник, здобудемо: , або
, або  .
. Порівнюючи коефіцієнти при однакових степенях
Порівнюючи коефіцієнти при однакових степенях 
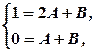 з якої знайдемо
з якої знайдемо  .
. .
.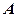 і
і  можна визначити інакше. Після того, як позбулися знаменника, змінній
можна визначити інакше. Після того, як позбулися знаменника, змінній  При
При  :
:  , звідки
, звідки 
 .
. :
:  , звідки
, звідки  ,
,  .
.
 - раціональну функцію, залежну від
- раціональну функцію, залежну від 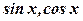 , якщо вона утворена з цих тригонометричних функцій та сталих за допомогою раціональних алгебраїчних дій.
, якщо вона утворена з цих тригонометричних функцій та сталих за допомогою раціональних алгебраїчних дій. приводяться до інтегралів від раціональної функції нового аргументу
приводяться до інтегралів від раціональної функції нового аргументу 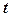 підстановкою
підстановкою , яка називається універсальною.
, яка називається універсальною. ,
,  ,
, 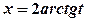 ,
,  .
. , тобто підінтегральна функція непарна відносно
, тобто підінтегральна функція непарна відносно 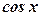 . Використовується підстановка
. Використовується підстановка  , тоді
, тоді  ,
,  ;
; - підінтегральна функція непарна відносно
- підінтегральна функція непарна відносно  .
. , тоді
, тоді  ,
,  ;
;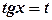 . При цьому використовуються формули:
. При цьому використовуються формули: ,
,  ,
,  ,
,  ;
; . Тут підінтегральна функція залежить раціональним образом тільки від
. Тут підінтегральна функція залежить раціональним образом тільки від  . Слід застосовувати підстановку
. Слід застосовувати підстановку  обчислюються за допомогою таких підстановок:
обчислюються за допомогою таких підстановок: ;
; ,
,  ;
; ,
,  ,
,  обчислюються за допомогою тригонометричних формул:
обчислюються за допомогою тригонометричних формул: ,
, ,
, .
. .
.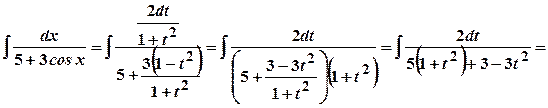
 .
.


