
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференціювання та інтегрування степеневих рядів.Содержание книги
Поиск на нашем сайте
1. Степеневі ряди можна почленно додавати і віднімати, причому, якщо ряд 2. Степеневі ряди можна множити за правилом множення многочленів, причому радіус збіжності ряду, отриманий в результаті множення, знову не менший меншого з чисел Для степеневих рядів справедливі такі теореми (приводимо їх без доведення): Теорема 1. Якщо степеневий ряд Теорема 2. Збіжний степеневий ряд можна почленно диференціювати в середині проміжку збіжності Це означає, що існують похідні Теорема 3. Збіжний степеневий ряд можна почленно інтегрувати в будь-якому проміжку, що лежить в середині області збіжності Нехай, наприклад, = звідки можна знайти, що Таким чином, степеневий ряд в своєму інтервалі збіжності по відношенню до операцій диференціювання та інтегрування веде себе так само, як многочлен із скінченною кількістю членів. Розглянемо, наприклад, розклад в ряд логарифмічної функції. Добре відомий ряд, який представляє собою суму членів нескінченно спадної геометричної прогресії Якщо цю рівність почленно проінтегрувати при З іншого боку Аналогічно можна представити дріб Звідси Але Причому, оскільки у прогресії ми покладали У випадку Представляючи функцію Однак, слід відмітити, що ряд для Віднявши від (5.7) розклад (5.8) і враховуючи рівність знаходимо За допомогою розкладу (5.9) вже можуть бути підраховані з будь-яким ступенем точності натуральні логарифми будь-яких додатніх чисел. Для цього досить дане число Оскільки знайдене значення Нехай Розглянемо розклад Щоб отримати цей розклад, досить в геометричній прогресії З іншої сторони
Ряди Тейлора і Маклорена. Якщо функція
то такий ряд називають рядом Тейлора, а вираз (66) називають розвиненням функції у степеневий ряд. Якщо у виразі (66)
і називається рядом Маклорена для функції Розлянемо приклади розвинення у степеневі ряди деяких елементарних функцій. Розвинути у степеневий ряд функцію функції:
При
Одержані значення підставимо у ряд Маклорена (67). Одержимо розвинення функції у степеневий ряд
Аналогічно можна знайти розвинення інших функцій у степеневі ряди. Так
Ряд (69) називають біноміальним рядом. Цей ряд збігається при Степеневі ряди мають широке застосування в точних та наближених обчисленнях функцій, інтегралів, наближеному розв’язуванні диференціальних рівнянь та інших випадках.
Приклад. Розкласти в степеневий ряд функцію Розв’язання. Позначимо
При підстановці замість
За формулою (65) знайдемо радіус збіжності одержаного ряду. Враховуючи, що коефіцієнти
Ряд збіжний на всій числовій осі
Приклад. Розкладаючи підінтегральну функцію в ряд обчислити з точністю до
Розв’язання. Підінтегральну функцію
Позначимо
Підставимо розвинення функції під знак інтеграла і після інтегрування обчислимо його наближено, взявши стільки членів, щоб решта ряду була меншою від
Відповідь.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 895; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.108.87 (0.008 с.) |

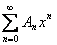 має радіус збіжності
має радіус збіжності 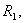 а ряд
а ряд 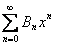 має радіус збіжності
має радіус збіжності  , то ряд
, то ряд 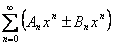 має радіус збіжності
має радіус збіжності  який не менший меншого з чисел
який не менший меншого з чисел 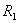 і
і  .
. , то його сума
, то його сума 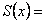
 де
де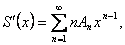
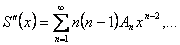 .
.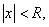 тоді
тоді
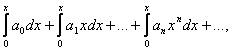
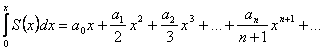 .
. , який збігається при
, який збігається при  до функції
до функції  , тобто
, тобто 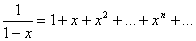 .
.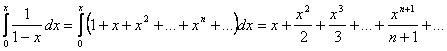
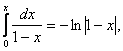 отже,
отже,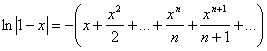 . (5.7)
. (5.7)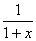 у вигляді
у вигляді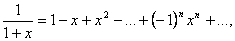 де
де 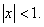
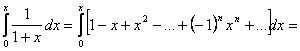
 .
.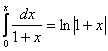 і, отже,
і, отже,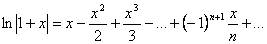 . (5.8)
. (5.8)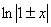 , отримані почленним інтегруванням, збігаються при
, отримані почленним інтегруванням, збігаються при 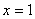 для функції
для функції  маємо, як це було показано раніше, умовно збіжний ряд
маємо, як це було показано раніше, умовно збіжний ряд .
.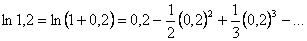 .
.
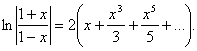 (5.9)
(5.9) представити у вигляді дробу
представити у вигляді дробу 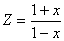 , звідки
, звідки  .
.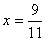 , знаходимо розклад в ряд
, знаходимо розклад в ряд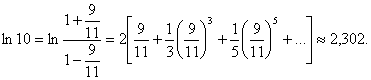

 . (5.10)
. (5.10)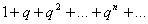 покласти
покласти 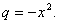 Почленно інтегруючи ряд (5.10), отримаємо
Почленно інтегруючи ряд (5.10), отримаємо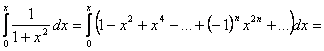
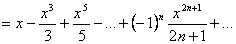 .
.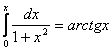 . Порівнюючи два значення інтеграла, отримуємо при
. Порівнюючи два значення інтеграла, отримуємо при 
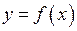 є сумою степеневого ряду
є сумою степеневого ряду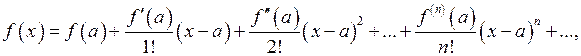 (66)
(66) , то такий ряд має вигляд
, то такий ряд має вигляд (67)
(67)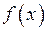 .
.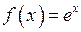 . Знайдемо похідні даної
. Знайдемо похідні даної
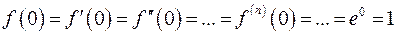 .
.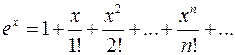 . (68)
. (68) ,
, ,
,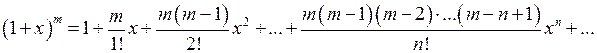 . (69)
. (69)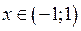 .
.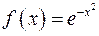 і знайти його радіус збіжності.
і знайти його радіус збіжності.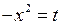 і для функції
і для функції 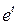 в силу формули (68) запишемо ряд
в силу формули (68) запишемо ряд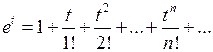 . (70)
. (70) його значення (
його значення ( ) ряд (70) матиме вигляд
) ряд (70) матиме вигляд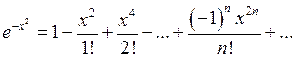 .
.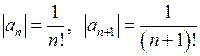 , тоді
, тоді ,
, .
.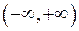 .
. визначений інтеграл
визначений інтеграл .
. розвинемо у біноміальний ряд, використовуючи формулу (69), яку перепишемо у вигляді
розвинемо у біноміальний ряд, використовуючи формулу (69), яку перепишемо у вигляді .
. ,
, 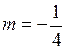 і одержимо таке розвинення для функції:
і одержимо таке розвинення для функції:


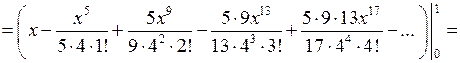

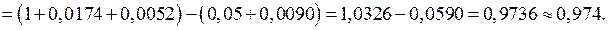
 .
.


