
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однорідні диференціальні рівнянняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Однорідними рівняннями першого порядку називають рівняння виду
Для того, щоб рівняння (39) звести до рівняння з відокремлюваними змінними, вводять заміну змінної
Змінні відокремлюються і його вже можна розв’язати.
Приклад. Знайти загальний розв’язок рівняння Розв’язання. Розв’яжемо це рівняння відносно похідної
Введемо заміну змінної
Або
якщо позначимо
Повернемося до старої змінної, тобто підставимо замість
Диференціальні рівняння у повних диференціалах Загальна теорія Якщо ліва частина диференціального рівняння
є повним диференціалом деякої функції
і, таким чином, рівняння приймає вигляд
є загальним інтегралом диференціального рівняння. Критерієм того, що рівняння є рівнянням в повних диференціалах, тобто необхідною та достатньою умовою, є виконання рівності
Нехай маємо рівняння в повних диференціалах. Тоді
Звідси
Звідси
Остаточно, загальний інтеграл має вигляд
Як відомо з математичного аналізу, якщо відомий повний диференціал
то
В цьому випадку одразу одержуємо розв’язок задачі Коші.
Множник, що Інтегрує В деяких випадках рівняння
не є рівнянням в повних диференціалах, але існує функція
вже буде рівнянням в повних диференціалах. Необхідною та достатньою умовою цього є рівність
або
Таким чином замість звичайного диференціального рівняння відносно функції
Після підстановки в рівняння маємо
або
Розділимо змінні
Проінтегрувавши і поклавши сталу інтегрування одиницею, одержимо:
Розглянемо частинні випадки. 1) Нехай І формула має вигляд
2) Нехай І формула має вигляд
3) Нехай
І формула має вигляд
4) Нехай І формула має вигляд
Зниження порядку деяких диференціальних рівнянь другого порядку Диференціальним рівнянням
Задача Коші для цього рівняння полягає у тому, щоб знайти розв’язок рівняння, який задовольняє умовам: Функція 1) Рівняння вигляду Розв’язок цього рівняння отримується
2) Диференціальне рівняння 3) Диференціальне рівняння вигляду Зразки розв’язування задач Приклад 1. Розв’язати рівняння:
Розв’язання. Права частина рівняння не містить невідомої функції
Отже, загальний розв’язок даного рівняння:
Приклад 2. Знайти загальний розв’язок рівняння:
Розв’язання. Дане рівняння того же типу, що і попереднє, тому його розв’язок знаходимо аналогічно, тобто:
За методом інтегрування частинами, маємо
Тоді загальний розв’язок рівняння має вигляд:
або
Ряди.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 646; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |

 . (39)
. (39) . Тоді
. Тоді  і рівняння (39) можна переписати через змінну
і рівняння (39) можна переписати через змінну  . Одержуємо
. Одержуємо
 .
. ; одержимо однорідне рівняння
; одержимо однорідне рівняння .
. . Одержимо
. Одержимо .
.
 , то одержимо вираз, який можна інтегрувати. Маємо
, то одержимо вираз, який можна інтегрувати. Маємо

 . Одержуємо загальний розв’язок у вигляді
. Одержуємо загальний розв’язок у вигляді

 , тобто
, тобто ,
, то рівняння називається рівнянням в повних диференціалах. Звідси вираз
то рівняння називається рівнянням в повних диференціалах. Звідси вираз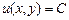


 де
де  - невідома функція. Для її визначення продиференціюємо співвідношення по
- невідома функція. Для її визначення продиференціюємо співвідношення по  і прирівняємо
і прирівняємо 

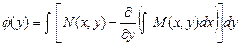 .
.
 і точку із змінними координатами
і точку із змінними координатами  . Більш зручно брати криву, що складається із двох відрізків прямих. В цьому випадку криволінійний інтеграл розпадається на два простих інтеграла
. Більш зручно брати криву, що складається із двох відрізків прямих. В цьому випадку криволінійний інтеграл розпадається на два простих інтеграла
 .
. така, що рівняння
така, що рівняння
 ,
, .
. одержимо диференціальне рівняння в частинних похідних відносно функції
одержимо диференціальне рівняння в частинних похідних відносно функції  . Задача інтегрування його значно спрощується, якщо відомо в якому вигляді шукати функцію
. Задача інтегрування його значно спрощується, якщо відомо в якому вигляді шукати функцію  де
де  - відома функція. В цьому випадку одержуємо
- відома функція. В цьому випадку одержуємо
 ,
,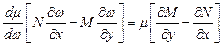 .
.
 .
. . Тоді
. Тоді 
 .
. . Тоді
. Тоді 

 . Тоді
. Тоді
 .
. . Тоді
. Тоді 
 .
. -го порядку називається рівняння вигляду
-го порядку називається рівняння вигляду 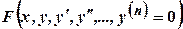 . Розв’язком такого рівняння називається будь-яка диференційована n разів функція
. Розв’язком такого рівняння називається будь-яка диференційована n разів функція  , яка перетворює дане рівняння на тотожність, тобто
, яка перетворює дане рівняння на тотожність, тобто .
.
 при
при  , де
, де  - числа, які називаються початковими умовами.
- числа, які називаються початковими умовами. називається загальним розв’язком даного диференціального рівняння
називається загальним розв’язком даного диференціального рівняння  ця функція є розв’язком будь-якої задачі Коші, що поставлена для цього рівняння. Будь-який розв’язок, який отриманий із загального розв’язку при конкретних значеннях сталих
ця функція є розв’язком будь-якої задачі Коші, що поставлена для цього рівняння. Будь-який розв’язок, який отриманий із загального розв’язку при конкретних значеннях сталих 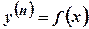 .
. - кратним інтегруванням, тобто:
- кратним інтегруванням, тобто: ,
, ,
,
 , де
, де .
. , що явно не містить шукану функцію
, що явно не містить шукану функцію  , за допомогою підстановки
, за допомогою підстановки  ;
;  зводять до відповідного рівняння першого порядку
зводять до відповідного рівняння першого порядку  . Розв’язок цього рівняння знаходять, виходячи з його типу, а потім, для отримання загального розв’язку початкового рівняння,
. Розв’язок цього рівняння знаходять, виходячи з його типу, а потім, для отримання загального розв’язку початкового рівняння, 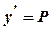 .
. , що явно не містить незалежну зміну
, що явно не містить незалежну зміну  , підстановкою
, підстановкою  зводять до диференціального рівняння першого порядку
зводять до диференціального рівняння першого порядку 
 .
. та її похідної
та її похідної  , тому для отримання розв’язку тричі послідовно інтегруємо обидві його частини:
, тому для отримання розв’язку тричі послідовно інтегруємо обидві його частини: ,
, ,
,
 .
. .
. .
. .
. ,
, ,
, ,
,
 =
=  .
. ,
, .
.


