
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7. Принцип можливих переміщень. Загальне рівняння динаміки.Содержание книги
Поиск на нашем сайте
Література [1] §112 – 116. [2] Гл.6 §1-4. На попередній лекції ми перейшли до вивчення основних принципів механіки, в яких міститься повна інформація про механічний рух і рівновагу механічної системи. Для розгляду наступного принципу необхідно розширити поняття в’язі, класифікувати в’язі, ввести додаткові поняття. § 7.1. Класифікація в’язей. Як відомо із “Статики”, невільні тіла відрізняються від вільних тим, що положення їх в просторі обмежені. Виявляється, що поняття в’язі більш широке. Означення: В’язь – це обмеження, накладені на координати, швидкості точок механічної системи, можуть залежати від часу.
В’язей може бути декілька, тоді індекс “ j ” – вказує номер в’язі. Нехай j =1,2.. s; тоді s - кількість в’язей. Зауважимо, що для того, щоб рух системи, яка складається з “n” точок, був можливий, треба щоб s<3n. На основі (7.1) можна провести класифікацію в’язей.
в противному разі – в’язь є не утримуючою, односторонньою. Покажемо це на прикладі. Механічна система складається з двох точок M1 і M2, з’єднаних абсолютно твердим стержнем довжиною l.
Стержень – двостороння (утримуюча), нитка – одностороння (не утримуюча) в’язь. 2). В’язь називають стаціонарною, якщо залежність (7.1) не включає час t. 3). В’язь називають геометричною, якщо залежність (7.1) обмежує тільки координати точок і не включає швидкостей точок. В противному разі в’язь називають кінематичною. 4). Якщо в залежності (7.1) швидкості точок можна виключити шляхом інтегрування, то в’язь називають кінематично–зінтегрованою. Кінематично-зінтегровані і геометричні в’язі утворюють клас голономних в’язей. Поділ в’язей на голономні і не голономні був запропонований німецьким фізиком Г. Герцом в монографії “Принципи механіки”, де він задавався метою показати, що загальні теореми можна отримати з одного принципу. Найчастіше в інженерній практиці зустрічаються геометричні стаціонарні в’язі. Наприклад:
Зверніть увагу, що кількість рівнянь це і є кількість в’язей! 2. Нерухомий шарнір в точці О.
3. При русі точки її координати задовольняють умову
Проінтегрувавши, отримаємо тобто в’язь – кінематично-зінтегрована.
Як записати рівняння в’язі? Самостійно. § 7.2. Можливі переміщення.
Уявимо собі, що ми зафіксували час (сфотографували точку в даному положенні). Задамося питанням: Які переміщення могла б здійснити точка М, залишаючись на поверхні? Таких переміщень багато. Позначимо їх Означення. Можливим переміщенням точки називають: - уявне, - нескінченно-мале переміщення, - дозволяється накладеними на точку в’язями в даний момент часу. Воно звичайно не залежить від сили Можливі переміщення механічної системи – це сукупність можливих переміщень точок системи, § 7.3. Число ступенів вільності.
Розглянемо систему, що складається з “n” точок; якщо система вільна - скільки координат визначають її положення в просторі? (відповідь – 3n). Незалежних можливих переміщень також 3n.
Скільки залишилось незалежних можливих переміщень, чи незалежних координат?
Приклад:
§ 7.4. Можлива робота. Ідеальні в ’ язі.
Вивчаючи теорему про зміну кінетичної енергії (тема 5), ми користувались поняттям “Ідеальні в’язі”. Там означення ідеальної в’язі було нестроге з математичної точки зору. Тепер є можливість це поправити. Французький математик Ж. Л. Лагранж ввів поняття ідеальної в’язі.
n - кількість реакцій в’язей,
До ідеальних відносять: всі геометричні в’язі без тертя, невагомий стержень, нерозтяжна нитка, нерухомий шарнір, а також в’язь, що забезпечує кочення без ковзання по шорсткій поверхні (§ 5.4.2). § 7.5. Принцип можливих переміщень. Сучасне формулювання принципу можливих переміщень було дане Лагранжем в 1788 році в результаті узагальнення теорії найпростіших механізмів (важеля, похилої площини, блоків і т.п.). Тому його називають принципом Лагранжа. Цей вчений, написав книгу “Аналітична механіка”, в якій немає ні одного рисунка. Він писав: “Всі, хто любить математику з задоволенням дізнаються, що механіка – галузь математики”.
Необхідність. Нехай механічна система, що складається з “n” матеріальних точок, знаходиться в рівновазі і на неї накладені геометричні, утримуючі, ідеальні, стаціонарні в’язі. Позначимо:
що і треба було довести. Достатність (самостійно довести). Увага! Рівнянь робіт (7.10) можна скласти стільки, скільки незалежних можливих переміщень, тобто скільки ступенів вільності має механічна система.
До речі, згадайте з курсу „Фізика” золоте правило механіки. Не впізнаєте його в (7.10’)? § 7.6. Застосування принципу можливих переміщень. § 7.6.1 Для визначення однієї з активних сил, що діють на систему з одним ступенем вільності. Пропонується послідовність дій, проілюстрована для конкретної задачі.
§ 7.6.2. Для визначення реакцій в’язі складеної конструкції. Згадаємо, як ми в «Статиці» визначали реакції в'язей конструкції, що складалась з великого числа зв'язаних між собою тіл.
Скільки рівнянь рівноваги треба скласти для визначення реакцій в'язей в точках А, В, Е та тиск в шарнірах С і D? (Відповідь) – дев'ять. З допомогою принципу можливих переміщень можна визначити одну із реакцій, або її складову вибірково! Тобто визначити, ту реакцію, яка нас «турбує» (потрібна), а не всі.
Як це робиться? Відкидають ту в'язь, реакцію якої треба визначити. Дію в'язі замінюють її реакцією, яку переводять в клас активних (заданих) сил. При цьому конструкція (яка не мала ступенів вільності – вона нерухома), отримує одну ступінь вільності. Далі діють так само, як і в § 7.6.1. Тобто - надають системі можливе переміщення; - складають рівняння робіт (7.10) (або потужностей (7.11)); - встановлюють зв’язок між можливими переміщеннями (чи швидкостями); - підставляють знайдені залежності між можливими переміщеннями (чи швидкостями) в рівняння п.м.п. і отримують шукану реакцію. § 7.7. Загальне рівняння динаміки, або принцип Д’Аламбера – Лагранжа.
Принцип Д’Аламбера – Лагранжа. В довільний момент руху механічної системи з ідеальними в’язями сума можливих робіт активних сил та сил інерції точок системи на будь-якому можливому переміщенні системи дорівнює нулеві. Рівняння (7.12) ще називають загальним рівнянням динаміки і складають їх стільки, скільки ступенів вільності. Для системи з голономними, двосторонніми, ідеальними в’язями з рівнянням (7.12) можна отримати загальні теореми динаміки, динамічні рівняння руху, тобто побувати теоретичний курс розділу “Динаміка”. Рекомендації до практичних занять на тему: „Застосування загального рівняння динаміки для складання динамічного рівняння руху практичної моделі механічної системи”.

 
  
 

 
Якщо серед в’язей є неідеальні в’язі, то їх реакції “переводять” в клас активних сил. Питання для самоконтролю.
17. Як формулюється принцип Д’Аламбера – Лагранжа?
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 748; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.87.167 (0.012 с.) |


 Рівняння в’язі
Рівняння в’язі
 1). В’язь називається утримуючою або двосторонньою, якщо вона описується рівнянням
1). В’язь називається утримуючою або двосторонньою, якщо вона описується рівнянням


 Рівняння цієї в’язі
Рівняння цієї в’язі
 Якщо замість стержня буде гнучка нерозтяжна нитка довжиною l, то координати точок M1 і M2 будуть задовольняти нерівність
Якщо замість стержня буде гнучка нерозтяжна нитка довжиною l, то координати точок M1 і M2 будуть задовольняти нерівність
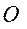












 1. На “n” точок системи накладена в’язь – площина Oxy.
1. На “n” точок системи накладена в’язь – площина Oxy.

 Які обмеження накладені на координати точок?
Які обмеження накладені на координати точок?
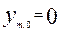








 Які обмеження накладені на координати точки О?
Які обмеження накладені на координати точки О?
 - двостороння стаціонарна кінематична в’язь.
- двостороння стаціонарна кінематична в’язь.





 4. На точку М (поршень) – накладена в’язь (напрямляючи) вздовж горизонталі.
4. На точку М (поршень) – накладена в’язь (напрямляючи) вздовж горизонталі.











 Нехай ми маємо точку, на яку накладена в’язь – поверхня.
Нехай ми маємо точку, на яку накладена в’язь – поверхня.





 Точка під дією деякої сили
Точка під дією деякої сили  . Нескінченно мале переміщення за час
. Нескінченно мале переміщення за час  -
-  , - можливе переміщення.
, - можливе переміщення. , бо уявне. В випадку стаціонарних в’язей дійсне переміщення одне з можливих.
, бо уявне. В випадку стаціонарних в’язей дійсне переміщення одне з можливих.  .
.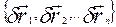 , де n - кількість точок. Таких сукупностей може бути багато, серед них є залежні між собою переміщення. Щоб з’ясувати скільки незалежних можливих переміщень, введемо нове поняття.
, де n - кількість точок. Таких сукупностей може бути багато, серед них є залежні між собою переміщення. Щоб з’ясувати скільки незалежних можливих переміщень, введемо нове поняття.







 Означення. Числом ступенів вільності механічної системи називають число незалежних її можливих переміщень.
Означення. Числом ступенів вільності механічної системи називають число незалежних її можливих переміщень.

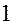 В випадку голономних в’язей число ступенів вільності визначається кількістю незалежних координат, які однозначно визначають положення точок системи у просторі.
В випадку голономних в’язей число ступенів вільності визначається кількістю незалежних координат, які однозначно визначають положення точок системи у просторі.
 Якщо на точки системи накладено “s” голономних в’язей, тобто маємо “s” залежностей між координатами.
Якщо на точки системи накладено “s” голономних в’язей, тобто маємо “s” залежностей між координатами.
 Існує зв’язок між можливими переміщеннями
Існує зв’язок між можливими переміщеннями
 (відповідь: (3n-s)) – позначимо літерою “р”.
(відповідь: (3n-s)) – позначимо літерою “р”.
 (7.3) – формула для визначення числа ступенів вільності системи, яка складається з “n” точок, на які накладено “s” голономних в’язей. Якщо маємо систему, яка знаходиться (рухається) в одній площині (не в просторі) формула (7.3) має вигляд:
(7.3) – формула для визначення числа ступенів вільності системи, яка складається з “n” точок, на які накладено “s” голономних в’язей. Якщо маємо систему, яка знаходиться (рухається) в одній площині (не в просторі) формула (7.3) має вигляд:
































 Кривошипно-шатунний механізм складається з трьох ланок: 1, 2, 3; скільки накладено в’язей? В точці О - дві, в точці В – одна, між точками О і А та А і В – одна, за формулою (7.4) маємо
Кривошипно-шатунний механізм складається з трьох ланок: 1, 2, 3; скільки накладено в’язей? В точці О - дві, в точці В – одна, між точками О і А та А і В – одна, за формулою (7.4) маємо  .
.


 т.Р – миттєвий центр швидкостей ланки АВ. Між можливими переміщеннями існують залежності:
т.Р – миттєвий центр швидкостей ланки АВ. Між можливими переміщеннями існують залежності:
 Означення. Можлива робота сили – робота сили на можливому переміщенні точки, в якій сила прикладена. Вона дорівнює скалярному добуткові модуля сили на можливе переміщення точки прикладання сили
Означення. Можлива робота сили – робота сили на можливому переміщенні точки, в якій сила прикладена. Вона дорівнює скалярному добуткові модуля сили на можливе переміщення точки прикладання сили 


 Або, аналогічно елементарній роботі (дивись формули (5.2, 5.3):
Або, аналогічно елементарній роботі (дивись формули (5.2, 5.3):
 Можлива робота моменту пари сил дорівнює (аналогічно 5.5)
Можлива робота моменту пари сил дорівнює (аналогічно 5.5)
 Означення. В’язі називаються ідеальними, якщо сума можливих робіт їх реакцій на будь-якому можливому переміщенні системи дорівнює нулеві, тобто
Означення. В’язі називаються ідеальними, якщо сума можливих робіт їх реакцій на будь-якому можливому переміщенні системи дорівнює нулеві, тобто - можливе переміщення точки прикладання сили реакції в’язі
- можливе переміщення точки прикладання сили реакції в’язі  .
.
 Принцип Лагранжа: Для рівноваги механічної системи з геометричними двосторонніми, ідеальними, стаціонарними в’язями необхідно і достатньо, щоб алгебраїчна сума можливих робіт всіх активних сил, що діють на систему, на будь-якому з її можливих переміщень дорівнювала нулеві, тобто
Принцип Лагранжа: Для рівноваги механічної системи з геометричними двосторонніми, ідеальними, стаціонарними в’язями необхідно і достатньо, щоб алгебраїчна сума можливих робіт всіх активних сил, що діють на систему, на будь-якому з її можливих переміщень дорівнювала нулеві, тобто - рівнодійна активних сил, що діють на „к”-ту точку,
- рівнодійна активних сил, що діють на „к”-ту точку, - рівнодійна реакцій в’язей, що діють на „к”-ту точку.
- рівнодійна реакцій в’язей, що діють на „к”-ту точку.

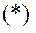 Оскільки система знаходиться в рівновазі, то кожна її точка також у рівновазі, а значить
Оскільки система знаходиться в рівновазі, то кожна її точка також у рівновазі, а значить
 Надамо системі одне з можливих переміщень і позначимо переміщення “к”-ої точки -
Надамо системі одне з можливих переміщень і позначимо переміщення “к”-ої точки - 
 Додамо “n” рядків (**)
Додамо “n” рядків (**)
 Враховуючи, що в’язі ідеальні, тобто має місце (7.9), в рівнянні (***) залишиться тільки перша сума
Враховуючи, що в’язі ідеальні, тобто має місце (7.9), в рівнянні (***) залишиться тільки перша сума

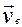




















 , або
, або  .
.

 де
де  - можлива швидкість точки прикладання сили
- можлива швидкість точки прикладання сили  .
.
 5) Залежність між можливими переміщеннями отримали раніше (див. рис.7.1)
При заданих геометричних параметрах ОА,
5) Залежність між можливими переміщеннями отримали раніше (див. рис.7.1)
При заданих геометричних параметрах ОА,  легко отримати розглядаючи трикутники АВР, ОВР, та АОВ.
легко отримати розглядаючи трикутники АВР, ОВР, та АОВ.
 Така ж сама залежність між швидкостями
Така ж сама залежність між швидкостями
 ,
,  , тому
, тому  отримали шуканий момент М.
отримали шуканий момент М.



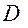


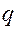































 Розглядаємо рух механічної системи, на яку накладені голономні, утримуючі ідеальні в’язі. На кожну точку
Розглядаємо рух механічної системи, на яку накладені голономні, утримуючі ідеальні в’язі. На кожну точку  і отримаємо
і отримаємо Надамо системі деяке можливе переміщення; кожна точка отримає своє переміщення
Надамо системі деяке можливе переміщення; кожна точка отримає своє переміщення 
 За визначенням ідеальних в’язей середній доданок дорівнює нулеві (формула (7.9)). Маємо принцип Д’Аламбера – Лагранжа
За визначенням ідеальних в’язей середній доданок дорівнює нулеві (формула (7.9)). Маємо принцип Д’Аламбера – Лагранжа







