
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Узагальнені координати – незалежні і однозначно визначають положення системи у просторі.Содержание книги
Поиск на нашем сайте
За аналогією до звичайних понять швидкості і прискорення маємо:
Одиниці їх вимірювання узгоджені з одиницями вимірювання узагальнених координат.
- зв’язок між можливими переміщеннями § 8.2. Узагальнені сили. Розглянемо механічну систему, що складається з “n” матеріальних точок і має “р” ступенів вільності. Нехай
Висновки: 1. Узагальнена сила є скалярною величиною. 2. Кожній узагальненій координаті відповідає своя узагальнена сила, тобто скільки узагальнених сил? (Відповідь. Стільки, скільки узагальнених координат, а значить скільки ступенів вільності має об’єкт вивчення).
Для визначення узагальненої сили на практиці формула (8.2) звичайно не підійде. § 8.2.1. Практичний спосіб обчислення 1). Задаємо можливі переміщення таким чином 2). Визначаємо суму можливих робіт активних сил на заданому переміщенні.
зауважимо, що Розглянемо приклад. На еліптичний маятник діють: сила Визначити:
Покажемо активні сили 1). Фіксуємо координату j=const. Задаємо 2).
§ 8.2.2. Обчислення узагальненої потенціальної сили.
Узагальнена потенціальна сила дорівнює взятій з протилежним знаком частинній похідній від потенціальної енергії по відповідній узагальненій координаті. Отримаємо принцип можливих переміщень та принцип Д’Аламбера–Лагранжа в узагальнених координатах, узагальнених силах. § 8.3. П ринцип можливих переміщень в узагальнених координатах.
Рівняння рівноваги в узагальнених силах:
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.158.84 (0.009 с.) |

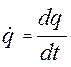 - узагальнена швидкість,
- узагальнена швидкість, - узагальнене прискорення.
- узагальнене прискорення.
 Оскільки наша мета отримати принципи механіки в узагальнених координатах, ми будемо говорити про можливу роботу, можливі переміщення. Можливі переміщення раніше
Оскільки наша мета отримати принципи механіки в узагальнених координатах, ми будемо говорити про можливу роботу, можливі переміщення. Можливі переміщення раніше  ,
,  ; тепер
; тепер 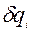 . Через те, що радіус-вектор “к”-ої точки є функція узагальнених координат для стаціонарних в’язей
. Через те, що радіус-вектор “к”-ої точки є функція узагальнених координат для стаціонарних в’язей 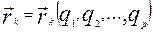 , то варіація
, то варіація 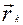 дорівнює
дорівнює і
і  - рівнодійна сил, що діють на “к”-ту точку. Надамо системі деяке можливе переміщення і визначимо можливу роботу всіх діючих на систему сил на цьому переміщенні
- рівнодійна сил, що діють на “к”-ту точку. Надамо системі деяке можливе переміщення і визначимо можливу роботу всіх діючих на систему сил на цьому переміщенні

 Враховуючи залежність (8.1), маємо
Враховуючи залежність (8.1), маємо
 Змінимо порядок підсумовування
Змінимо порядок підсумовування
 Якщо порівняти (б) з (а), то бачимо, що обидві вони визначають роботу діючих на систему сил і можна зробити висновок, що вирази, які знаходяться в дужках рівність (б) відіграють роль сил, бо
Якщо порівняти (б) з (а), то бачимо, що обидві вони визначають роботу діючих на систему сил і можна зробити висновок, що вирази, які знаходяться в дужках рівність (б) відіграють роль сил, бо 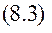
 Маємо можливу роботу в узагальнених силах
Маємо можливу роботу в узагальнених силах 3. Одиниці виміру узагальнених сил диктуються одиницями виміру узагальнених координат.
3. Одиниці виміру узагальнених сил диктуються одиницями виміру узагальнених координат. - “j”-ої узагальненої сили.
- “j”-ої узагальненої сили. . Тобто фіксуємо всі координати крім “j”-ої. (Нагадаю, що всі
. Тобто фіксуємо всі координати крім “j”-ої. (Нагадаю, що всі 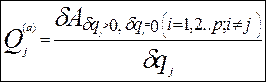
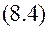 3). Тоді формула (8.3) має один доданок, тобто
3). Тоді формула (8.3) має один доданок, тобто  , і загальна сила дорівнює
, і загальна сила дорівнює (додатна!))
(додатна!)) ,
,  ,
,  - сили ваги тіл А і В, АВ=l. Узагальнені координати q1=x, q2=φ.
- сили ваги тіл А і В, АВ=l. Узагальнені координати q1=x, q2=φ. - узагальнену активну силу, що відповідає координаті х;
- узагальнену активну силу, що відповідає координаті х;
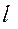
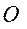






















 - узагальнену активну силу, що відповідає координаті j.
- узагальнену активну силу, що відповідає координаті j. . Сума можливих робіт активних сил на цьому переміщенні дорівнює
. Сума можливих робіт активних сил на цьому переміщенні дорівнює  , тому
, тому 
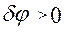 .
. 
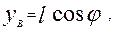

 тому
тому 
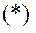
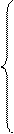
 В потенціальному стаціонарному силовому полі проекції потенціальної сили виражаються через потенціальну енергію таким чином:
В потенціальному стаціонарному силовому полі проекції потенціальної сили виражаються через потенціальну енергію таким чином: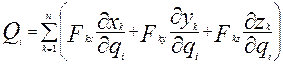 Але потенціальна енергія в стаціонарному полі – функція положення, тому
Але потенціальна енергія в стаціонарному полі – функція положення, тому 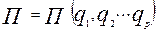 . Застосуємо формулу (8.2), згадавши, чому дорівнює скалярний добуток двох векторів через координати цих векторів
. Застосуємо формулу (8.2), згадавши, чому дорівнює скалярний добуток двох векторів через координати цих векторів 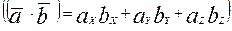
 Для потенціальних сил з врахуванням (*), маємо
Для потенціальних сил з врахуванням (*), маємо
 тобто:
тобто:
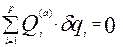 Згадаємо цей принцип. Розглядається механічна система, що знаходиться в рівновазі. На систему накладені голономні утримуючі ідеальні в’язі. Тоді сума можливих робіт активних сил дорівнює нулеві на будь-якому можливому переміщенні системи. І навпаки, якщо
Згадаємо цей принцип. Розглядається механічна система, що знаходиться в рівновазі. На систему накладені голономні утримуючі ідеальні в’язі. Тоді сума можливих робіт активних сил дорівнює нулеві на будь-якому можливому переміщенні системи. І навпаки, якщо  то механічна система при таких в’язях знаходиться в рівновазі. Враховуючи (8.3) перепишемо принцип
то механічна система при таких в’язях знаходиться в рівновазі. Враховуючи (8.3) перепишемо принцип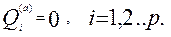
 Бачимо, що доданків в цій сумі менше, бо p<3n (р=3n-s). Але справа не тільки в кількості доданків. Справа в тому, що всі можливі переміщення
Бачимо, що доданків в цій сумі менше, бо p<3n (р=3n-s). Але справа не тільки в кількості доданків. Справа в тому, що всі можливі переміщення 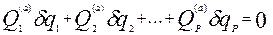 , якщо
, якщо 


