
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 5. Теорема про зміну кінетичної енергії механічної системи.Содержание книги
Поиск на нашем сайте
Література [1] §58 – 71. [2] Гл.4 §5.
Якщо маси точок однакові то: - кількість руху цієї системи - момент кількості руху відносно довільної точки О також дорівнює нулеві, бо То введених динамічних мір руху не достатньо. Треба ще одну. Давайте спробуємо підрахувати
Саме тому, що кількість руху є векторна величина, а кінетична енергія - скалярна, між вченими багато років продовжувалась полеміка. Кількість руху Механічний рух має дві міри: якщо механічний рух перетворюється в механічний, то міра – кількість руху; якщо механічний рух переходить в інші види рухів, наприклад тепловий, то його мірою є кінетична енергія. Отже, є дві різні міри механічного руху: § 5.1. Робота і потужність сили та пари сил. Означення: Робота сили – це фізична величина, яка характеризує дію сили на матеріальний об’єкт на деякому переміщенні. Елементарна робота сили – робота сили на елементарному переміщенні. Нехай рух точки М, до якої прикладена сила
де
Зауважимо на те, що елементарну роботу позначаємо З поняттям роботи пов’язане поняття потужності.
   Означення Потужність – це величина, яка визначає роботу сили за одиницю часу, тобто Означення Потужність – це величина, яка визначає роботу сили за одиницю часу, тобто
Так само елементарна робота сили, прикладеної до тіла, яке має вісь обертання, дорівнює добуткові моменту сили відносно осі обертання на елементарний кут повороту тіла.
Знак елементарної роботи і потужності сили диктується формулами (5.2) та (5.4) в залежності від кута
§5.2. Приклади обчислення робіт.
де Є такі сили, робота яких визначається, якщо відомі положення, початкове і кінцеве, точки прикладання сили і не залежать від траєкторії руху точки їх прикладання. Такі сили називаються потенціальними. До таких належить: сила ваги (сила тяжіння), сила пружності. §5.2.1. Робота сили тяжіння (сили ваги). Нехай точка М, вагою
де (Z0 – Z1) – різниця висот між початковим і кінцевим положенням. Позначимо її
де знак “+” беремо, якщо Z0 > Z1, тобто при опусканні точки М, знак “-” при підйомі. Якщо Z0 = Z1, то робота дорівнює нулеві. Робота сили §5.2.2. Робота сили пружності.
l 0 - довжина недеформованої пружини.
§5.2.3. Робота постійної сили.
В залежності від кута - додатньою, якщо 0< - від’ємною, якщо 90о< - дорівнює нулеві, якщо §5.3. Кінетична енергія.
Знати швидкість кожної точки практично неможливо. Існує теорема, за якою визначається кінетична енергія системи при її складному русі. §5.3.1. Теорема Кьоніга про кінетичну енергію. Нехай механічна система здійснює складний рух: - переносний рух разом з системою координат, що рухається поступально відносно нерухомої системи координат з швидкістю центру мас - відносний рух відносно Кьонігової системи координат (розглядали таку систему координат в попередній темі).
Добуток
бо Теорема Кьоніга. Кінетична енергія системи при її складному русі, якщо відносний рух – відносно Кьонігової системи координат, дорівнює сумі кінетичних енергій центру мас, в якому зосереджена маса всієї системи, та кінетичної енергії системи при її відносному русі. Перейдемо до визначення кінетичної енергії твердих тіл, з яких складаються практичні моделі механічних систем. §5.3.2. Кінетична енергія твердих тіл. а) Тіло здійснює поступальний рух. Тоді, як відомо, швидкості усіх точок, з яких складається тіло, в кожну мить однакові. Швидкість “к”-ої точки дорівнює швидкості тіла.
Кінетична енергія тіла – сума кінетичних енергій точок
в) Тіло здійснює плоско-паралельній рух. Плоско-паралельний рух тіла, як відомо, є складний рух: - переносний – поступальний разом з сисмтемою координат, яка рухається з швидкістю - відносний – обертальний навколо осі, яка проходить через точку С.
Кінетична енергія при плоско-паралельному русі – сума кінетичних енергій поступального руху разом з центром мас і обертального руху навколо рухомої осі, яка проходить через центр мас, перпендикулярно до основної площини.
Де §5.4. Теорема про зміну кінетичної енергії. Вивчаємо рух теоретичної моделі механічної системи, що складається з “n” точок. Розглянемо рух матеріальної точки, яка належить до М.С.
  На неї діють сили: На неї діють сили:  - зовнішня сила, - зовнішня сила,  - активна сила - активна сила
Маємо
бо Теорема. Похідна по часу від кінетичної енергії механічної системи дорівнює сумі потужностей сил, що діють на систему (зовнішніх та внутрішніх; або активних та реакцій в’язей).
Бачимо, що зміни кількості руху та кінетичного моменту залежать тільки від зовнішніх сил. А кінетична енергія? Дивись формулу (5.19). Є такі випадки, коли робота (чи потужність) внутрішніх сил дорівнює нулеві. Розглянемо ці випадки. §5.4.1. Теорема в випадку незмінюваної механічної системи.
Те ж саме має місце і для інших точок системи. Висновок. В випадку незмінюваної механічної системи сума робіт усіх внутрішніх сил, що діють на систему, дорівнює нулеві. Тому в формулі (5.18) залишиться робота тільки зовнішніх сил, а в (5.19) потужність тільки зовнішніх сил. §5.4.2. Теорема в випадку системи з ідеальними в’язями. Розглянемо рух механічної системи, на яку накладені в ’ язі, що не змінюються з часом. Якщо сума елементарних робіт реакцій в’язей, які накладені на систему, дорівнює нулеві такі в ’ язі називають ідеальними. (Загальне, більш точніше, поняття ідеальних в’язей буде визначено пізніше).
Приклади ідеальних в’язей 1). Абсолютно гладенька поверхня.
2). Нерухомий шарнір без тертя.
3). Нерозтяжна нитка, нерозтяжний стержень.
| ||||||||||
|
| Поделиться: |




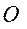




 Пропонується Вам такий приклад механічної системи: маємо дві точки, які рухаються назустріч одна одній з однаковою швидкістю.
Пропонується Вам такий приклад механічної системи: маємо дві точки, які рухаються назустріч одна одній з однаковою швидкістю.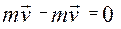 ,
, .
. . Що це за міра? (Кінетична енергія.)
. Що це за міра? (Кінетична енергія.)





 Кінетична енергіяє завжди додатною і не залежить від напрямку руху точки.
Кінетична енергіяє завжди додатною і не залежить від напрямку руху точки. запропонована Декартом в 1644 р., а “жива сила”
запропонована Декартом в 1644 р., а “жива сила”  в 1686 р. Лейбніцем. Чітке тлумачення про міри механічного руху було дано Ф. Енгельсом в кінці XIX ст. в його праці “Діалектика природи”.
в 1686 р. Лейбніцем. Чітке тлумачення про міри механічного руху було дано Ф. Енгельсом в кінці XIX ст. в його праці “Діалектика природи”. , а це означає, що повинні існувати дві різні міри дії сили: імпульс сили
, а це означає, що повинні існувати дві різні міри дії сили: імпульс сили 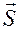 (§3.2) і робота сили.
(§3.2) і робота сили. , визначається векторним способом
, визначається векторним способом 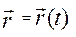















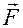

 Означення. Елементарна робота сили дорівнює скалярному добутку вектора сили на елементарне переміщення точки, до якої прикладена сила.
Означення. Елементарна робота сили дорівнює скалярному добутку вектора сили на елементарне переміщення точки, до якої прикладена сила.
 Або, інакше
Або, інакше - проекція сили на дотичну до траєкторії в точці М,
- проекція сили на дотичну до траєкторії в точці М,  , коли
, коли  .
.
 Якщо рух точки М задано координатним способом, тоді скалярний добуток
Якщо рух точки М задано координатним способом, тоді скалярний добуток  виразимо через координати співмножників
виразимо через координати співмножників 
 , а не
, а не  , оскільки взагалі вона не є повним диференціалом.
, оскільки взагалі вона не є повним диференціалом.


















 Елементарна робота пари сил. Нехай до тіла прикладена пара сил
Елементарна робота пари сил. Нехай до тіла прикладена пара сил  з моментом М, пара обертає тіло навколо осі Oz.
з моментом М, пара обертає тіло навколо осі Oz.  дорівнює
дорівнює 

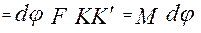 , бо
, бо  дорівнює моментові пари М.
дорівнює моментові пари М.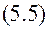
 Елементарна робота пари сил дорівнює добуткові момента пари сил на елементарний кут
Елементарна робота пари сил дорівнює добуткові момента пари сил на елементарний кут  .
.
 Потужність момента пари сил, чи момента сили, прикладеної до тіла, що обертається навколо осі, дорівнює
Потужність момента пари сил, чи момента сили, прикладеної до тіла, що обертається навколо осі, дорівнює між векторами сили і швидкості.
між векторами сили і швидкості.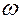
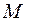
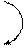



 Знак елементарної роботи і потужності момента пари сил залежить від того, чи співпадають напрямки момента і кутової швидкості: якщо співпадають знак “+”, якщо ні “-”.
Знак елементарної роботи і потужності момента пари сил залежить від того, чи співпадають напрямки момента і кутової швидкості: якщо співпадають знак “+”, якщо ні “-”.
 Робота сили на скінченому переміщенні, наприклад від точки М0 до точки М1 (Рис.5.3) складається з суми елементарних робіт, яка є інтегральною сумою, тобто
Робота сили на скінченому переміщенні, наприклад від точки М0 до точки М1 (Рис.5.3) складається з суми елементарних робіт, яка є інтегральною сумою, тобто є одна з формул (5.1), (5.2), (5.3), (5.5). Робота сили в загальному випадку залежить від характеру руху точки, до якої вона прикладена.
є одна з формул (5.1), (5.2), (5.3), (5.5). Робота сили в загальному випадку залежить від характеру руху точки, до якої вона прикладена. , перемістилась з положення М0 (x0, y0, z0) в положення М1 (x1, y1, z1). Визначимо роботу сили ваги на цьому переміщенні. Для цього скористаємось формулою (5.7), де елементарну роботу підставимо з (5.3).
, перемістилась з положення М0 (x0, y0, z0) в положення М1 (x1, y1, z1). Визначимо роботу сили ваги на цьому переміщенні. Для цього скористаємось формулою (5.7), де елементарну роботу підставимо з (5.3).


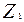
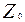













 Отримаємо:
Отримаємо: .
.

 Остаточно
Остаточно не залежить від траєкторії точки М.
не залежить від траєкторії точки М.



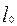










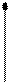





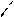







 За законом Гука сила пружності
За законом Гука сила пружності 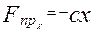 , де с – коефіцієнт жорсткості, його розмірність
, де с – коефіцієнт жорсткості, його розмірність  , x – деформація пружини. Нехай під дією
, x – деформація пружини. Нехай під дією 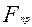 точка М перемістилась з положення М0 в положення М1; x0, x1 – початкова та кінцева деформація пружини. Тоді скористаємось формулою (5.7), та (5.3):
точка М перемістилась з положення М0 в положення М1; x0, x1 – початкова та кінцева деформація пружини. Тоді скористаємось формулою (5.7), та (5.3):














 Цей самий результат можна отримати за допомогою графіка залежності Fx від х, бо робота сил пружності є площа трапеції, заштрихованої на Рис.5.7.
Цей самий результат можна отримати за допомогою графіка залежності Fx від х, бо робота сил пружності є площа трапеції, заштрихованої на Рис.5.7.



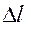









 Нехай до точки М, що рухається по прямій, прикладена сила
Нехай до точки М, що рухається по прямій, прикладена сила 
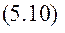 Робота сили
Робота сили 
 Кінетична енергія механічної системи, яка складається з “n” точок - це арифметична сума кінетичних енергій точок системи.
Кінетична енергія механічної системи, яка складається з “n” точок - це арифметична сума кінетичних енергій точок системи. .
.


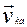























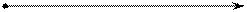
 Осі O1 x1 y1 z1– нерухомі,
Осі O1 x1 y1 z1– нерухомі, Осі C x y z – рухаються поступально з швидкістю
Осі C x y z – рухаються поступально з швидкістю 


 Тоді абсолютна швидкість “к”-ої точки дорівнює
Тоді абсолютна швидкість “к”-ої точки дорівнює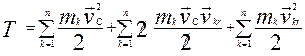 Згідно з (5.11),
Згідно з (5.11), , бо радіус-вектор центру мас відносно центру мас дорівнює нулеві.
, бо радіус-вектор центру мас відносно центру мас дорівнює нулеві.
 Маємо
Маємо - кінетична енергія системи при її відносному русі.
- кінетична енергія системи при її відносному русі.
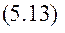
 Маємо, кінетичну енергію тіла, як суму кінетичних енергій точок, з яких воно складається
Маємо, кінетичну енергію тіла, як суму кінетичних енергій точок, з яких воно складається  ,
,  –маса тіла.
–маса тіла.














 , але швидкість кожної точки дорівнює
, але швидкість кожної точки дорівнює  , тому
, тому  ,
,
 бо
бо  - осьовий момент інерції тіла.
- осьовий момент інерції тіла.
 Застосуємо теорему Кьоніга, враховуючи, що при відносному обертальному русі
Застосуємо теорему Кьоніга, враховуючи, що при відносному обертальному русі  . Тоді
. Тоді
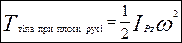 Як відомо, при плоскому русі в кожну мить існує точка, швидкість якої дорівнює нулеві – миттєвий центр швидкостей (точка Р). Тому, замість формули (5.15), можна скористатись формулою (5.14)
Як відомо, при плоскому русі в кожну мить існує точка, швидкість якої дорівнює нулеві – миттєвий центр швидкостей (точка Р). Тому, замість формули (5.15), можна скористатись формулою (5.14) - момент інерції відносно осі Pz; яка паралельна центральній осі Cz, тому
- момент інерції відносно осі Pz; яка паралельна центральній осі Cz, тому  , згідно теореми Гюйгенса – Штейнера.
, згідно теореми Гюйгенса – Штейнера.











 - реакція в’язі.
- реакція в’язі.
 Запишемо основний закон динаміки точки
Запишемо основний закон динаміки точки Через те, що нас цікавить, як зміниться кінетична енергія, яка залежить від швидкості
Через те, що нас цікавить, як зміниться кінетична енергія, яка залежить від швидкості  , то перепишемо (а) враховуючи, що
, то перепишемо (а) враховуючи, що  , і домножимо ліву частину на
, і домножимо ліву частину на  , а праву на
, а праву на  . Маємо
. Маємо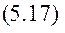
 але:
але:  ,
,  - елементарна робота сили
- елементарна робота сили  . Тоді
. Тоді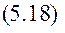
 Це має місце для всіх точок системи к = 1,2..n. Якщо додамо всі “n” рядків, отримаємо
Це має місце для всіх точок системи к = 1,2..n. Якщо додамо всі “n” рядків, отримаємо
 - кінетична енергія системи.
- кінетична енергія системи.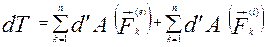

 Поділимо (5.18) на
Поділимо (5.18) на  :
: - потужність сили
- потужність сили 
 Згадаємо дві попередні теореми
Згадаємо дві попередні теореми











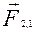
 Якщо відстань між точками механічної системи з часом не змінюється, то система називається незмінюваною (прикладом є тверде тіло).
Якщо відстань між точками механічної системи з часом не змінюється, то система називається незмінюваною (прикладом є тверде тіло).

 Розглянемо суму елементарних робіт внутрішніх сил
Розглянемо суму елементарних робіт внутрішніх сил  та
та 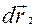 та
та 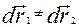 , а сума елементарних робіт сил
, а сума елементарних робіт сил 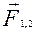 та
та  Внутрішні сили, як відомо, рівні за модулем, та протилежні за напрямком, тобто
Внутрішні сили, як відомо, рівні за модулем, та протилежні за напрямком, тобто  . Тоді маємо згадавши, чому дорівнює скалярний добуток векторів
. Тоді маємо згадавши, чому дорівнює скалярний добуток векторів Як відомо з “Кінематики твердого тіла”, має місце теорема про проекції швидкостей двох точок тіла на пряму, що їх з’єднує, тобто
Як відомо з “Кінематики твердого тіла”, має місце теорема про проекції швидкостей двох точок тіла на пряму, що їх з’єднує, тобто





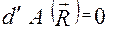 Реакція перпендикулярна до поверхні, тому елементарна робота реакції дорівнює нулеві
Реакція перпендикулярна до поверхні, тому елементарна робота реакції дорівнює нулеві


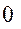





 Реакція прикладена в нерухомій точці, тому нема переміщення
Реакція прикладена в нерухомій точці, тому нема переміщення 






