
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сили в розділі “Динаміка”. Приклади.Содержание книги
Поиск на нашем сайте
Основна задача розділу “Динаміка” – встановити зв’язок діючих сил з кінематичними характеристиками руху матеріальних об’єктів. Назвемо динамічними рівняннями руху – рівняння, які зв’язують між собою характеристики: Інерційні (маса, моменти інерції), 2. геометричні, конструктивні (кількість тіл, кути, радіуси, в’язі...), Кінематичні (час, швидкості, прискорення, положення), Міри взаємодії (сили, моменти пар сил). Тобто це будуть залежності такого вигляду
При всій різноманітності задач, які “Динаміка” розв’язує, можна виділити дві основні задачі. Перша задача: за даними інерційними, конструктивними та кінематичними характеристиками визначити сили. Друга задача: за даними інерційними, конструктивними характеристиками та силами, що діють на об’єкт визначити кінематичні характеристики. § 1.2. Закони класичної механіки.
Другий закон – основний. Згадайте цей закон. Зверніть увагу на те, що не можна формулювати його так: Прискорення, з яким рухається матеріальна точка, пропорційне прикладеній до точки силі, обернено пропорційне масі, спрямоване вздовж сили.
Перші два закони мають місце в інерціальній системі відліку! Третій закон (закон дії протидії)– два тіла взаємодіють між собою з силами рівними за модулем і протилежним за напрямком.
Маса – міра інертності тіла при поступальному русі. Інертність – властивість тіла зберігати стан спокою, чи рівномірного прямолінійного руху. Між масою і вагою тіла є зв’язок
(Чисельна величина прискорення вільного падіння g змінюється в залежності від положення тіла на Землі Поряд з “інертною масою” в механіці є “маса тяжіння”, яка входить в закон всесвітнього тяжіння. Доведено, що чисельні величини цих мас однакові. Одиниці вимірювання: [m] = кг, [F] = H, [a] = м/с2 Почнемо з найпростішого об’єкту вивчення. Динаміка точки. § 1.3. Диференціальні рівняння руху матеріальної точки. Дві задачі динаміки точки. (Скільки способів завдання руху в “Кінематиці”? відповідь - три)
 }, к= 1,2... }, к= 1,2...
Згадаємо, що при Осі координат Декартові, При природному векторному способі тому в “Кінематиці” способі завдання руху завдання руху точки її задати рух – це задати точки відомі радіус – вектор функція координати
Для точки з масою рівняння(1.3), осі Ox,Oy,Oz, врахувавши, координат при цьому враховуючи, що маємо:
Маючи Д.Р.Р. точки в одному з видів (1.5), (1.6), (1.7) можна розв’язати дві основні задачі динаміки точки. 1. Відомі кінематичні рівняння руху точки заданої маси. Визначити одну з сил, що діє на точку (перша задача динаміки). 2. Відомі сили, що діють на точку в довільний момент часу і маса точки. Визначити кінематичні рівняння руху точки при заданих початкових умовах (друга задача динаміки). Рекомендації для практичних занять на тему “Друга задача динаміки точки” Розглянемо, наприклад, рух точки в площині Oxy. Пропонується така послідовність дій. 1. Вибираємо систему відліку (осі координат, t=0) і показуємо точку в довільному положенні. 2. Виходячи з умови задачі, формулюємо початкові умови, тобто записуємо значення проекції початкової швидкості на осі 3. На рисунку показуємо сили, які діють на точку в довільному положенні
4. 5. Інтегруємо складені диференціальні рівняння; якщо права частина рівняння (тобто сили) постійна, залежить від часу, чи швидкості методом поділу змінних; якщо сила – функція координат, то можна ввести заміну 6. При інтегруванні, звичайно, виникають постійні інтегрування; для того щоб їх визначити користуються початковими умовами.
Зауваження. Диференціальні рівняння руху невільної матеріальної точки відрізняються від Д.Р.Р. вільної точки наявністю в правих частинах рівнянь (1.5) ÷ (1.7) реакцій в’язей, які, звичайно, невідомі. Тому на практиці осі координат краще вибирати так, щоб реакції в’язей не проектувалися на ці осі. Питання для самоконтролю. 1. Запишіть диференціальні рівняння руху матеріальної точки в декартових координатах. 2. Які рівняння називаються диференціальними рівняннями руху точки в натуральній формі? 3. Сформулюйте першу основну задачу динаміки матеріальної точки. 4. Яка сутність другої основної задачі динаміки матеріальної точки? 5. Як визначають постійні інтегрування диференціальних рівнянь руху матеріальної точки? Динамікамеханічної системи. Тема 2. Вступ до “Динаміки механічної системи”. Означення: Механічна система – це сукупність матеріальних точок (часто тіл), в якій положення, або рух кожної залежить від положення, або руху, решти. Взаємодіють між собою елементи механічної системи за законом рівності дії протидії. Розрізняють моделі механічної системи: 1.
 теоретична вільна; теоретична вільна;
2. теоретична невільна; 3. практична (завжди невільна) – складається з тіл; 4. незмінна – така модель, в якої відстані між точками не змінюються; Основна мета розділу “Динаміка“ в технічному ВУЗі: навчитись складати динамічні рівняння практичних моделей (Д.Р.Р.).
§ 2.1. Структурні та інерційні характеристики механічної системи.
Момент інерції механічної системи відносно деякого геометричного елемента (точки, осі, площини) називається сума добутків мас точок системи на квадрат їх відстаней до даного елемента. Не позначаючи відносно чого момент інерції маємо для системи, яка складається з n точок:
Якщо маса системи розподілена неперервно (наприклад, тверде тіло), то має місце формула:
де dm – маса елементарного об’єму; h – відстань цього об’єму до точки, чи до осі, чи до площини; v – об’єм тіла. Запишемо формули моментів інерції системи, що складається з n точок (рис. 2.1): – Полярний відносно точки О: – Осьовий відносно осі Оz: – Відцентровий: Зауваження. 1. Пізніше Ви переконаєтесь, що моменти інерції – це є міри інертності тіл, що виконують обертальні рухи. 2. Важливим буде знаходити такі осі для обертання тіл, відносно яких відцентрові моменти інерції дорівнюють нулеві. Наприклад Ixz=Iyz=0. Тоді вісь Оz називається головною!
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.152.153 (0.008 с.) |
























 ,
, 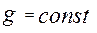 в даній точці Землі.
в даній точці Землі.







 , ω – частота струму.
, ω – частота струму. 













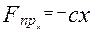 , с – коефіцієнт жорсткості пружини.
, с – коефіцієнт жорсткості пружини.










 - формула Стокса.
- формула Стокса.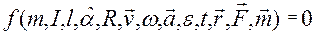


 Перший закон.Матеріальна точка зберігає стан спокою, або рівномірного прямолінійного руху доти, поки дія інших тіл не змінить цей стан.
Перший закон.Матеріальна точка зберігає стан спокою, або рівномірного прямолінійного руху доти, поки дія інших тіл не змінить цей стан. , бо змінюється суть. Треба починати з прискорення, а не з сили, бо причиною прискорення є сила.
, бо змінюється суть. Треба починати з прискорення, а не з сили, бо причиною прискорення є сила.

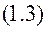
 Якщо декілька сил діють на точку, то, звичайно, замість однієї сили буде сума сил, тобто
Якщо декілька сил діють на точку, то, звичайно, замість однієї сили буде сума сил, тобто
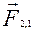



 Зверніть увагу, що йдеться про два тіла
Зверніть увагу, що йдеться про два тіла
 В другому законі ми зустрілися з поняттям маса
В другому законі ми зустрілися з поняттям маса
 )
)


 , - траєкторія
, - траєкторія






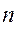
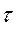




 часу
часу  ,
,  - дугова координата
- дугова координата 








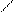
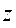











 з початком відрахунку
з початком відрахунку Спроціювавши (1.3) на Згадаємо, що осі
Спроціювавши (1.3) на Згадаємо, що осі що
що  ,
,  ,
,  були такі:
були такі: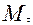 - дотична
- дотична - головна нормаль
- головна нормаль - бінормаль
- бінормаль






 ,
,  та початкові координати xo, yo
та початкові координати xo, yo
 Складаємо Д.Р.Р. точки. Для прикладу
Складаємо Д.Р.Р. точки. Для прикладу 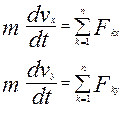
 , а потім інтегрувати.
, а потім інтегрувати.

 (2.1)
(2.1)





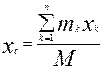













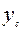













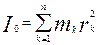 – осьовий:
– осьовий:  – відцентровий:
– відцентровий: 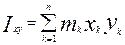




 ;
; ;
;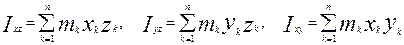 .
.


