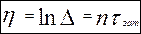Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 12. Вплив лінійного опору на лінійні власні коливання системи з одним ступенем вільності.Содержание книги
Поиск на нашем сайте
Література[2] Гл. 7 § 2. [4] § 11.3 [3] § 9 § 12.1. Узагальнена сила опору. Функція Релея. Нехай на кожну точку системи діє сила опору, яка залежить від першого ступеня швидкості точки.
де Визначимо узагальнену силу опору, скориставшись формулою узагальненої сили (8.2)
Тоді
Введемо функцію Релея, яка вперше була запропонована Джоном Релеєм в 1878 р. в книзі “Теорія звуку”
Тоді узагальнена сила опору має вигляд
Узагальнена сила опору, що відповідає “і”- тій узагальненій координаті, дорівнює взятій з протилежним знаком частинній похідній по відповідній узагальненій швидкості від функції Релея. Функція Ф за своєю структурою аналогічна кінетичній енергії, де замість мас точок mk стоять коефіцієнти опору βk. Виразимо функцію Ф через
З’ясуємо фізичний зміст функції Релея без доведення
При дії сил опору повна енергія механічної системи Е зменшується, розсіюється, тому функцію Ф називають ще функцією розсіювання. Висновок. Подвійна функція Релея вимірює швидкість розсіювання повної механічної енергії. § 12.2. Постановка задачі. Диференціальне рівняння руху. Розглянемо рух М.С. з одним ступенем вільності поблизу положення стійкої рівноваги. На систему діють потенціальні сили і сили лінійного опору. Положення системи в довільний момент часу визначається координатою q. Кінетична і потенціальна енергія системи має наближене значення в вигляді (10.5) та (10.7) Дисипативну функцію (12.4) отримаємо також в наближеному вигляді, для цього функцію В(q) розкладемо в ряд Маклорена
Оскільки утримуються члени другого порядку малості, достатньо в ряді (12.6) залишити перший доданок В(0). Позначимо В(0)=b – узагальнений коефіцієнт опору. Тоді
Складемо диференціальне рівняння руху системи з допомогою рівняння Лагранжу другого роду (10.3), де Qнепотенц. – є узагальнена сила опору.
Похідні мають такий вигляд
Поділимо на
Диференціальне рівняння руху з врахуванням введених позначень буде таким
§ 12.3. Інтегрування диференціального рівняння руху. Рівняння (12.8) – лінійне однорідне диференціальне рівняння з постійними коефіцієнтами. Згадаємо, як виглядає характеристичне рівняння
Корені характеристичного рівняння
Мають місце три випадки 1. 2. 3. Розглянемо ці випадки. 1. Випадок малого опору Позначимо Розв’язок диференціального рівняння (12.8) має вигляд
де С1, С2 – постійні інтегрування. Перейдемо до амплітудної форми (як ми робили в § 11.3)
Тоді
Скористаємось початковими умовами для визначення постійних С1 та С2. Для цього отримаємо швидкість в довільний момент часу
При t=0:
Відповідно постійні А та α дорівнюють згідно з (12.11)
§ 12.4. Властивості руху при малому опорі. Щоб з’ясувати, як змінюється координати q(t) з часом побудуємо її графік, скориставшись (12.12). Для синусоїди обмежуючими будуть криві 1 та 2
Умовним періодом буде період функції
Виразимо
Для дуже малого опору, коли
Він виражає темп затухання умовних амплітуд.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.91.15 (0.006 с.) |

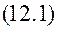
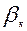 - коефіцієнт опору середовища.
- коефіцієнт опору середовища.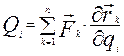
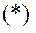 Підставимо значення сили опору (12.1), а також врахуємо тотожність Лагранжа
Підставимо значення сили опору (12.1), а також врахуємо тотожність Лагранжа 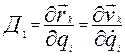
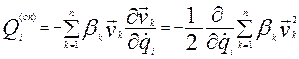
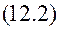
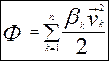
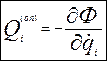
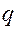 та
та 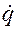 для системи з одним ступенем
для системи з одним ступенем  вільності, аналогічно кінетичній енергії
вільності, аналогічно кінетичній енергії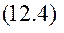
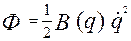 , де
, де 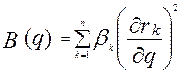
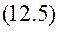

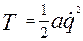 ,
, 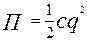 (відповідно)
(відповідно)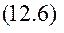
 .
.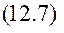
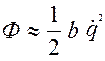

 ,
, 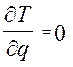 ,
, 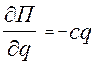 ,
,  . Тому диференціальне рівняння руху має вигляд
. Тому диференціальне рівняння руху має вигляд
 і введемо позначення
і введемо позначення 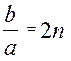 ,
, 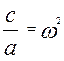 . Згадаємо, що
. Згадаємо, що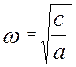 - кругова частота власних коливань без врахування сил опору. Величину
- кругова частота власних коливань без врахування сил опору. Величину 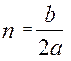 називають коефіцієнт затухання.
називають коефіцієнт затухання.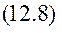
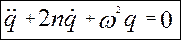

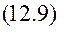

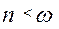 - випадок малого опору.
- випадок малого опору.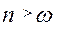 - випадок великого опору.
- випадок великого опору. - випадок критичного опору.
- випадок критичного опору. , тоді
, тоді 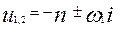

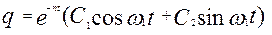

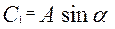 ,
,  ,
, 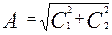 ,
, 
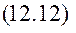
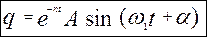
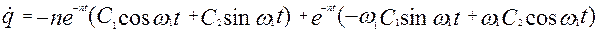

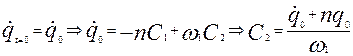
 ,
, 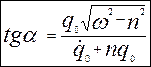 .
.




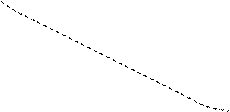

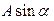

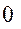

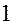













 З графіка функції q(t) бачимо, що величини послідовних найбільших відхилень від положення рівноваги зменшується з часом, прагнучи до нуля. Тому рух, який визначається рівняннями (12.10) чи (12.12) називають затухаючими коливаннями.
З графіка функції q(t) бачимо, що величини послідовних найбільших відхилень від положення рівноваги зменшується з часом, прагнучи до нуля. Тому рух, який визначається рівняннями (12.10) чи (12.12) називають затухаючими коливаннями.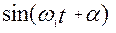 , тобто
, тобто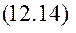
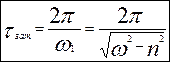

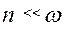 ,
, 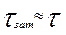 .
.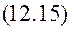 Змінну величину
Змінну величину 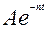 називають умовною амплітудою затухаючих коливань. Вона зменшується за законом спадної геометричної прогресії. Величину відношення двох послідовних максимумів називають декрементом коливань.
називають умовною амплітудою затухаючих коливань. Вона зменшується за законом спадної геометричної прогресії. Величину відношення двох послідовних максимумів називають декрементом коливань.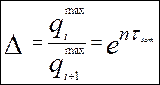
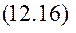 Натуральний логарифм декремента називають логарифмічним декрементом коливань
Натуральний логарифм декремента називають логарифмічним декрементом коливань