
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 13. Вимушені коливання механічної системи з одним ступенем вільності (без врахування опору).Содержание книги
Поиск на нашем сайте
Література: [2] Гл. 7. §2. [4] Гл. 11.3. [3] §6–8. § 13.1. Постановка задачі. Вимушеними називають коливання під дією: зовнішніх періодичних сил, або періодичних переміщень.
де Н – амплітуда, р – частота, δ – початкова фаза узагальненої збурюючої сили. Кінетична і потенціальна енергії системи мають вигляд
с – коефіцієнт жорсткості. Згадаємо метод вивчення коливань (§ 10.3): 1. Скласти диференціальні рівняння руху; 2. Проінтегрувати диференціальні рівняння руху; 3. Вивчити властивості руху. § 13.2. Диференціальне рівняння вимушених коливань.
§ 13.3. Рівняння (закон) руху.
де:
Вигляд
Звідси:
Висновок з формули (13.9) Власні коливання складаються з двох рухів: – амплітуда першого з них (перші два доданки) залежить від початкових умов; – амплітуда другого руху залежить як від параметрів системи (бо Цікавий факт! Навіть при нульових початкових умовах власні коливання з частотою ω мають місце. § 13.4. Властивості вимушених коливань.
Властивості: 1). Рух гармонійний, періодичний з частотою р збурюючої сили. 2). Амплітуда – залежить від параметрів системи с і а (бо
де
де
На рис. 13.3 випадкові резонансу відповідає одна точка (коли z=1), δ=π/2 Побудуємо графік залежності модуля амплітуди вимушених коливань від коефіцієнту розладнання
1) Якщо р<ω, Авим.>0, максимуму сили відповідає максимум координати. На рис. 13.4 суцільна лінія – Qзб., пунктирна qвим.. 2) Якщо p> ω, Ми розглянули закон і властивості руху для випадку, коли р≠ω, тобто частота збурюючої сили і частота власних коливань не співпадають. § 13.5. Випадок резонансу.
Тоді (13.12):
Це косинусоїда з змінними зростаючими амплітудами. Властивості руху: 1. При резонансі коливання відбуваються з наростаючою за законом арифметичної прогресії амплітудою.
2. Порівняємо фази сили і координати координата сила
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.30.222 (0.008 с.) |

































 В першому випадку кажуть про силове збудження. Наприклад. В практиці віброобробки застосовується вібромашина (Рис. 1.). Мета: відшліфувати деталі, зняти з них заусениці. За рахунок ексцентрика, маса якого m, створюється збурююча сила F=mω 2 l, проекції якої на осі координат – періодичні функції аргументу ωt; наприклад Fy=mω 2 lsin(ωt+δ).
В першому випадку кажуть про силове збудження. Наприклад. В практиці віброобробки застосовується вібромашина (Рис. 1.). Мета: відшліфувати деталі, зняти з них заусениці. За рахунок ексцентрика, маса якого m, створюється збурююча сила F=mω 2 l, проекції якої на осі координат – періодичні функції аргументу ωt; наприклад Fy=mω 2 lsin(ωt+δ).







 Прикладом кінематичного збудження є хвилеподібна форма дороги (Рис. 13.2).
Прикладом кінематичного збудження є хвилеподібна форма дороги (Рис. 13.2). 

 Розглядаються малі рухи механічної системи поблизу положення стійкої рівноваги. Діють сили: крім потенціальних, збурюючі періодичні. Нехай узагальнену силу, що відповідає вибраній узагальненій координаті q ми визначимо
Розглядаються малі рухи механічної системи поблизу положення стійкої рівноваги. Діють сили: крім потенціальних, збурюючі періодичні. Нехай узагальнену силу, що відповідає вибраній узагальненій координаті q ми визначимо
 а – коефіцієнт інерції,
а – коефіцієнт інерції,
 Скористаємось рівнянням Лагранжу ІІ роду (§ 10.3), де Qнепотенц. – є узагальнена збурюючи сила.
Скористаємось рівнянням Лагранжу ІІ роду (§ 10.3), де Qнепотенц. – є узагальнена збурюючи сила.
 Похідні ми знаходили раніше
Похідні ми знаходили раніше  ,
,  . Узагальнена потенціальна сила дорівнює
. Узагальнена потенціальна сила дорівнює  ,
,  . Таким чином, маємо
. Таким чином, маємо Поділимо ліву і праву частини рівняння (13.3) на коефіцієнт інерції а та введемо позначення:
Поділимо ліву і праву частини рівняння (13.3) на коефіцієнт інерції а та введемо позначення:  (згадаємо що ω – це частота власних коливань).
(згадаємо що ω – це частота власних коливань).
 Тоді диференціальне рівняння має вигляд
Тоді диференціальне рівняння має вигляд
 Отримаємо, проінтегрувавши (13.4). Що це за рівняння з точки зору математики? Відповідь: ЛНДР – лінійне неоднорідне диференціальне рівняння ІІ порядку з постійними коефіцієнтами. Його загальний розв’язок є сума розв’язків
Отримаємо, проінтегрувавши (13.4). Що це за рівняння з точки зору математики? Відповідь: ЛНДР – лінійне неоднорідне диференціальне рівняння ІІ порядку з постійними коефіцієнтами. Його загальний розв’язок є сума розв’язків – загальний розв’язок однорідного рівняння;
– загальний розв’язок однорідного рівняння; – частинний розв’язок неоднорідного рівняння.
– частинний розв’язок неоднорідного рівняння.
 . Маємо, прирівнявши коефіцієнти при sin(pt+δ)
. Маємо, прирівнявши коефіцієнти при sin(pt+δ)



 тобто
тобто
 Закон руху, згідно з (13.5) має вигляд
Закон руху, згідно з (13.5) має вигляд З початкових умов визначимо постійні С1 та С2. Для цього отримаємо швидкість в довільний момент часу.
З початкових умов визначимо постійні С1 та С2. Для цього отримаємо швидкість в довільний момент часу. При t=0
При t=0 Маємо закон руху з врахуванням початкових умов
Маємо закон руху з врахуванням початкових умов Пам’ятаємо, що
Пам’ятаємо, що 
 ) так і від параметрів збурюючої сили Н, р, δ.
) так і від параметрів збурюючої сили Н, р, δ.
 Вимушені коливання це ті, що відбуваються з частотою збурюючої сили, тобто р. Закон вимушених коливань – це власне q*.
Вимушені коливання це ті, що відбуваються з частотою збурюючої сили, тобто р. Закон вимушених коливань – це власне q*. Дослідимо формулу амплітуди більш детально, а саме винесемо з знаменника ω2.
Дослідимо формулу амплітуди більш детально, а саме винесемо з знаменника ω2. – назвемо коефіцієнтом розладнання (расстройки на рос. мові).
– назвемо коефіцієнтом розладнання (расстройки на рос. мові).
 Введемо поняття коефіцієнта динамічності
Введемо поняття коефіцієнта динамічності – коефіцієнт динамічності.
– коефіцієнт динамічності.











 3). Якщо p→ ω, Авим прагне до нескінченності. Якщо p<< ω, Авим малі, тобто збурюючі сили з великими частотами безпечні.
3). Якщо p→ ω, Авим прагне до нескінченності. Якщо p<< ω, Авим малі, тобто збурюючі сили з великими частотами безпечні.



 Розглянемо зсув фази коливань по відношенню до збурюючої сили. Для цього перепишемо вирази збурюючої сили і закону вимушених коливань.
Розглянемо зсув фази коливань по відношенню до збурюючої сили. Для цього перепишемо вирази збурюючої сили і закону вимушених коливань. – координата з силою в противофазі. Тобто має місце залежність на рис. 13.5
– координата з силою в противофазі. Тобто має місце залежність на рис. 13.5
 Це випадок, коли p=ω (частоти збурюючої сили і власних коливань співпадають). В цьому випадку розв’язок диференціального рівняння руху (13.4) шукають в іншому вигляді, а саме
Це випадок, коли p=ω (частоти збурюючої сили і власних коливань співпадають). В цьому випадку розв’язок диференціального рівняння руху (13.4) шукають в іншому вигляді, а саме
 Через те, що (13.12) – розв’язок рівняння (13.4), підставимо його в це диференціальне рівняння, отримавши спочатку похідні
Через те, що (13.12) – розв’язок рівняння (13.4), підставимо його в це диференціальне рівняння, отримавши спочатку похідні
 Після підстановки маємо
Після підстановки маємо  , тобто
, тобто  .
.
 Загальний розв’язок згідно (13.5)
Загальний розв’язок згідно (13.5)












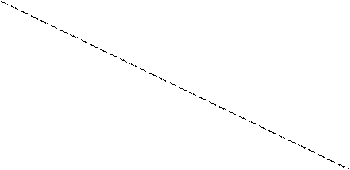
 Звичайно, останній доданок зростає з часом, його графік і побудуємо
Звичайно, останній доданок зростає з часом, його графік і побудуємо

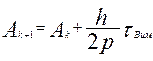
 ;
; .
.










 Фази відрізняються на
Фази відрізняються на  , тобто якщо сила досягає максимуму, координата – мінімуму і навпаки. На рис. 13.7 знову суцільна лінія – збурюючи сила, пунктирна – координата.
, тобто якщо сила досягає максимуму, координата – мінімуму і навпаки. На рис. 13.7 знову суцільна лінія – збурюючи сила, пунктирна – координата.


