
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Теорема про зміну кінетичного моменту. Динамічні рівняння руху твердих тіл.Содержание книги
Поиск на нашем сайте
Література: [1] § 55-57, [2] Гл.4 § 4. Згадаємо 3 приклади руху тіл, масою М. 1.
2. Плоско-паралельний рух колеса, що котиться:
3. Обертальний рух колеса навколо центральної осі СZ:
Визначимо кількість руху в цих випадках: в першому випадку і в другому Висновок: Кількість руху – міра тільки поступального руху! Це не є універсальна міра руху. Треба вводити інші динамічні міри. Зокрема, для обертального руху - це буде момент кількості руху, або інша назва - кінетичний момент. §4.1 Кінетичний момент матеріальної точки та механічної системи.
§4.1.1 Кінетичний момент відносно центру. Згадаємо: коли ми мали справу з моментом?
Аналогічно введемо поняття момент кількості руху матеріальної точки відносно центру О. Маємо точку масою
Вектор
§4.1.2. Кінетичний момент відносно осі.
Аналогічно введемо поняття момент кількості руху (кінетичний момент) матеріальної точки відносно осі.
Між кінетичними моментами є зв’язок такий самий, як між моментами сили. А саме:
Для практики важливо знати кінетичний момент твердого тіла при його обертальному русі навколо осі, відносно цієї осі.
і перша міра руху, яку ми ввели – кількість руху тіла §4.2. Кінетичний момент тіла відносно осі обертання.
Вектор кількості руху точки mk за модулем дорівнює
Означення. Кінетичний момент твердого тіла, що обертається навколо нерухомої осі, відносно осі обертання дорівнює добуткові моменту інерції тіла відносно цієї осі на кутову швидкість тіла. Порівняємо формули кількості руху (3.2) і кінетичного моменту (4.7)
Висновок: Маса – міра інертності тіла, що рухається поступально. Осьовий момент інерції – міра інертності тіла, що обертається навколо осі. Зауваження. Для випадку обертання тіла навколо довільної осі кінетичні моменти відносно інших осей не дорівнюють нулеві, а дорівнюють §4.3. Теорема про зміну кінетичного моменту.
 Тепер нас цікавить питання: який зв’язок між мірами руху Тепер нас цікавить питання: який зв’язок між мірами руху  та мірами взаємодії та мірами взаємодії
Тоді продовжимо викладки: Через те, що друга сума дорівнює нулеві (Чому?) маємо: Теорема. Похідна по часу від кінетичного моменту механічної системи відносно деякого центра дорівнює геометричній сумі моментів всіх зовнішніх сіл, що діють на систему, відносно даного центра.
(Сформулювати самостійно). § 4.4. Диференціальні рівняння простих рухів. З “Кінематики” відомо, що до простих рухів твердого тіла відносяться поступальний рух і обертальний рух навколо нерухомої осі.
Таким чином, рівняння (4.10) – динамічні рівняння поступального руху твердого тіла. Отримаємо динамічне рівняння обертального руху тіла навколо нерухомої осі, скориставшись теоремою (4.9), враховуючи (4.7)
Індекс “е” можна опустити і в рівняннях (4.10) і в (4.11), бо йдеться про сили, що діють на тіло, звичайно, ззовні.
§4.5. Динамічні рівняння плоско–паралельного руху твердого тіла.
Динамічні рівняння поступального руху ми вже маємо, це рівняння (4.10). Скористатись динамічними рівняннями обертального руху (4.1111) нема підстави, бо вісь Сz при плоскому русі є рухомою віссю. Тому розглянемо наступну теорему. §4.5.1. Теорема про зміну кінетичного моменту механічної системи при відносному русі.
Теорема. Похідна по часу від кінетичного моменту механічної системи при її відносному русі відносно центру мас геометрично дорівнює головному моментові зовнішніх сил, що діють на систему, відносно центру мас (мається на увазі відносний рух по відношенню до Кьонігової системи координат).
Порівняйте з (4.8). §4.5.2. Динамічні рівняння плоского руху.
З формули (4.9) аналогічно маємо, якщо Отже, якщо сума моментів зовнішніх сил, що діють на систему, відносно деякого центра (або осі) дорівнює нулеві, то кінетичний момент системи відносно цього центра (або осі) не змінюється. Це закони збереження кінетичних моментів. Приклади:
при збільшенні моменту інерції системи, кутова швидкість зменшується. Цю умову наглядно демонструють на “стільці Жуковського” – горизонтальній платформі яка може обертатись навколо вертикальної осі при дуже малому терті. Якщо на платформі знаходиться людина і вона обертається навколо осі, то зовнішніми силами є тільки сили ваги і реакція опори. Сума моментів зовнішніх сил відносно осі обертання дорівнює нулеві, а тому 2). При розкачуванні качелі, присідаючи і піднімаючись людина збільшує і зменшує момент інерції відносно осі обертання; відповідно змінюється і кутова швидкість.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.61.184 (0.008 с.) |




 Поступальний рух:
Поступальний рух:




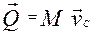 , в третьому випадку
, в третьому випадку  ).
).

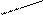
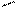




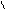






 В розділі “Статика”- це був момент сили відносно центру і відносно осі.
В розділі “Статика”- це був момент сили відносно центру і відносно осі.


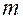 , вектор кількості її руху
, вектор кількості її руху  прикладений в цій точці (Рис. 4.1).
прикладений в цій точці (Рис. 4.1).









 Означення: Моментом кількості руху (кінетичним моментом) точки відносно центра О (Рис. 4.1) називаємо векторний добуток радіуса-вектора точки на її кількість руху.
Означення: Моментом кількості руху (кінетичним моментом) точки відносно центра О (Рис. 4.1) називаємо векторний добуток радіуса-вектора точки на її кількість руху.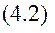 Модуль
Модуль 
 і центр О.
і центр О.


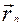






























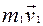
















 Означення: Моментом кількості руху (кінетичним моментом) механічної системи відносно центра О називається геометрична сума кінетичних моментів всіх точок механічної системи відносно даного центра.
Означення: Моментом кількості руху (кінетичним моментом) механічної системи відносно центра О називається геометрична сума кінетичних моментів всіх точок механічної системи відносно даного центра.










 Знову згадаємо момент сили відносно осі:
Знову згадаємо момент сили відносно осі:























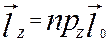








 Проекція кінетичного моменту матеріальної точки відносно деякого центру на вісь, яка проходить через цей центр, дорівнює кінетичному моментові точки відносно цієї осі.
Проекція кінетичного моменту матеріальної точки відносно деякого центру на вісь, яка проходить через цей центр, дорівнює кінетичному моментові точки відносно цієї осі.
 Означення: Кінетичним моментом механічної системи відносно осі називається алгебраїчна сума кінетичних моментів точок системи відносно цієї ж осі.
Означення: Кінетичним моментом механічної системи відносно осі називається алгебраїчна сума кінетичних моментів точок системи відносно цієї ж осі.






 Пам’ятаєте був розглянутий випадок:
Пам’ятаєте був розглянутий випадок: , дорівнювала нулеві. Подивимось, чому дорівнює кінетичний момент цього тіла відносно осі обертання.
, дорівнювала нулеві. Подивимось, чому дорівнює кінетичний момент цього тіла відносно осі обертання.











 Розглянемо випадок механічної системи – тверде тіло, яке обертається навколо нерухомої осі
Розглянемо випадок механічної системи – тверде тіло, яке обертається навколо нерухомої осі 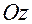 з кутовою швидкістю
з кутовою швидкістю  ,бо з “Кінематики” відомо, що:
,бо з “Кінематики” відомо, що: 
 Вектор
Вектор  лежить в площині, перпендикулярній до осі обертання.
лежить в площині, перпендикулярній до осі обертання.
 Тому кінетичний момент механічної системи – твердого тіла, яке складається з “n” точок відносно осі Oz, згідно з (4.6), дорівнює:
Тому кінетичний момент механічної системи – твердого тіла, яке складається з “n” точок відносно осі Oz, згідно з (4.6), дорівнює:
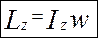 Оскільки
Оскільки  - момент інерції тіла відносно осі Oz, то формула (а) набуває вигляду:
- момент інерції тіла відносно осі Oz, то формула (а) набуває вигляду: - міра поступального руху.
- міра поступального руху. - міра обертального руху тіла навколо центральної головної осі. Центральна головна вісь – вісь, відносно якої відцентрові моменти інерції
- міра обертального руху тіла навколо центральної головної осі. Центральна головна вісь – вісь, відносно якої відцентрові моменти інерції  .
. ,
, 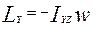 .
. Згадаємо першу загальну теорему – про зміну кількості руху (3.4)..
Згадаємо першу загальну теорему – про зміну кількості руху (3.4)..








 Візьмемо похідну від кінетичного моменту відносно центру О, враховуючи формулу (4.3):
Візьмемо похідну від кінетичного моменту відносно центру О, враховуючи формулу (4.3): 


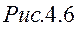
 - основний закон динаміки “к”-ої точки, к=1,2..n
- основний закон динаміки “к”-ої точки, к=1,2..n


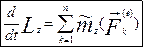
 Спроєціювавши векторну рівність (4.8) на вісь Оz, маємо теорему відносно осі
Спроєціювавши векторну рівність (4.8) на вісь Оz, маємо теорему відносно осі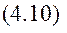




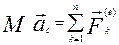 При поступальному русі всі точки тіла рухаються однаково. Тому диференціальні рівняння руху центра мас тіла є диференціальними рівняннями поступального руху тіла. Спроектувавши векторну рівність (3.3) на осі координат, маємо
При поступальному русі всі точки тіла рухаються однаково. Тому диференціальні рівняння руху центра мас тіла є диференціальними рівняннями поступального руху тіла. Спроектувавши векторну рівність (3.3) на осі координат, маємо

 Якщо
Якщо  ,то маємо
,то маємо
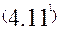
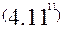 Рівнянню (4.11) можна придати інших форм, враховуючи, що
Рівнянню (4.11) можна придати інших форм, враховуючи, що 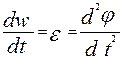

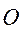











 Як відомо, з розділу “Кінематика”, замість вивчення плоско–паралельного руху тіла, вивчають рух тіла площиною, паралельною основній нерухомій площині Н, тобто перерізу S в своїй площині.
Як відомо, з розділу “Кінематика”, замість вивчення плоско–паралельного руху тіла, вивчають рух тіла площиною, паралельною основній нерухомій площині Н, тобто перерізу S в своїй площині.
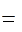












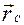
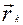










 Розглядаємо рух механічної системи відносно двох систем координат: О1х1у1z1 – нерухомої та Схуz – рухомої, що рухається поступально по відношенню до нерухомої системи координат О1х1у1z1 (така система координат називається Кьоніговою).
Розглядаємо рух механічної системи відносно двох систем координат: О1х1у1z1 – нерухомої та Схуz – рухомої, що рухається поступально по відношенню до нерухомої системи координат О1х1у1z1 (така система координат називається Кьоніговою).
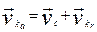 Тоді, як відомо, абсолютна швидкість кожної точки
Тоді, як відомо, абсолютна швидкість кожної точки  є векторна сума переносної швидкості
є векторна сума переносної швидкості  (вона дорівнює швидкості точки С) та відносної швидкості точки
(вона дорівнює швидкості точки С) та відносної швидкості точки  .
.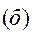
 Радіуси–вектори “к”–ої точки зв’язані такою формулою
Радіуси–вектори “к”–ої точки зв’язані такою формулою Визначимо кінетичний момент механічної системи, яка складається з “n” точок, відносно центру О
Визначимо кінетичний момент механічної системи, яка складається з “n” точок, відносно центру О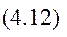
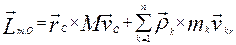 Покажемо, що два середніх доданки дорівнюють нулеві, через те, що
Покажемо, що два середніх доданки дорівнюють нулеві, через те, що  (дивись формулу (2.1)), а радіус–вектор центру мас
(дивись формулу (2.1)), а радіус–вектор центру мас  відносно самого себе (т.С) дорівнює нулеві. З тієї ж причини
відносно самого себе (т.С) дорівнює нулеві. З тієї ж причини  . Тоді
. Тоді
 Тут
Тут 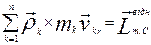 . Згадаємо формулу (4.8)
. Згадаємо формулу (4.8)  і візьмемо похідну по часу від лівої і правої частин формули (4.12). Тоді маємо
і візьмемо похідну по часу від лівої і правої частин формули (4.12). Тоді маємо
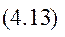 В лівій частині рівності (с) запишемо суму моментів сил
В лівій частині рівності (с) запишемо суму моментів сил  – відносно точки О, згадавши означення вектору – моменту сили відносно точки (розділ “Статика”), а саме
– відносно точки О, згадавши означення вектору – моменту сили відносно точки (розділ “Статика”), а саме  , де
, де  :
:  , або
, або
 Спроєціювавши (4.13) на вісь, що проходить через точку С, наприклад Сz, отримаємо
Спроєціювавши (4.13) на вісь, що проходить через точку С, наприклад Сz, отримаємо
 На переріз тіла S діють сили
На переріз тіла S діють сили  (звичайно вони є зовнішніми); маса тіла М. Динамічні рівняння плоского руху отримаємо, скориставшись динамічними рівняннями поступального руху (4.10) в пло
(звичайно вони є зовнішніми); маса тіла М. Динамічні рівняння плоского руху отримаємо, скориставшись динамічними рівняннями поступального руху (4.10) в пло  щині хОу, та теоремою про зміну
щині хОу, та теоремою про зміну  кіне
кіне 


 русі – обертальному навколо рухомої осі Сz
русі – обертальному навколо рухомої осі Сz  (4.14). При цьому вважаємо, що форма тіла
(4.14). При цьому вважаємо, що форма тіла  відома і осьовий момент інерції тіла також відомий, тому кінетичний момент тіла від
відома і осьовий момент інерції тіла також відомий, тому кінетичний момент тіла від  носно осі Сz дорівнює LCz=ICzω.
носно осі Сz дорівнює LCz=ICzω. Таким чином, динамічні
Таким чином, динамічні  рівняння плоского руху мають вигляд:
рівняння плоского руху мають вигляд: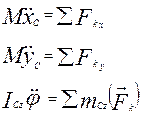
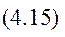 Самостійно. Записати зміст першої та другої задачі динаміки твердого тіла, що здійснює плоский рух.
Самостійно. Записати зміст першої та другої задачі динаміки твердого тіла, що здійснює плоский рух. §4.6. Наслідки теорем. Закони збереження кінетичних моментів.
§4.6. Наслідки теорем. Закони збереження кінетичних моментів.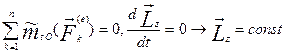 З формули (4.8) випливає що, якщо
З формули (4.8) випливає що, якщо 1). При обертанні тіла навколо нерухомої осі, якщо його форма (а значить, осьовий момент інерції змінюється), то зміниться і кутова швидкість.
1). При обертанні тіла навколо нерухомої осі, якщо його форма (а значить, осьовий момент інерції змінюється), то зміниться і кутова швидкість. тобто
тобто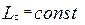 . Змінюючи положення рук (змінюється осьовий момент інерції) людина змінює кутову швидкість.
. Змінюючи положення рук (змінюється осьовий момент інерції) людина змінює кутову швидкість.


