
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механічна енергія консервативної системи при її русі не змінюється.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рекомендації до практичних занять на тему “ Теорема про зміну кінетичної енергії”. 1). Рівняння теореми в інтегральному виді (5.21) дозволяє розв’язувати ті задачі, в яких в число даних і невідомих величин входять: 1. сили; 2. переміщення точок чи тіл системи; 3. швидкості тіл. При цьому діючі сили повинні бути постійними, або залежати тільки від переміщень. 2). Рівняння теореми в диференціальній формі (5.18’), (5.19) можна використати для складання динамічних рівнянь руху практичної моделі. При цьому на механічну систему можуть діяти змінні сили, які залежать від часу, швидкості, переміщення. Питання для самоконтролю. 1. Назвіть дві міри механічного руху. За якими формулами вони розраховуються? 2. Що називається роботою сил? 3. Запишіть три формули, за допомогою яких можна розрахувати елементарну роботу сили. 4. Чому дорівнює робота рівнодійної системи сил? 5. Що називається потужністю сисли? 6. В паспорті електродвигуна вказано його потужність N = 2 кВт і частоту обертання n = 900 об/хв. Який момент створується на валі двигуна? 7. Сформулюйте теорему Кьоніга. 8. Запишіть дві формули, за допомогою яких можна розрахувати кінетичну енергію системи. 9. За якою формулою розраховується кінетична енергія твердого тіла, що здійснює плоскопаралельний рух? 10. Сформулюйте теорему про зміну кінетичної енергії точки в диференціальній формі. 11. Сформулюйте теорему про зміну кінетичної енергії механічної системи в інегральній (кінцевій) формі. 12. Запишіть рівняння, яке виражає теорему про зміну кінетичної енергії твердого тіла. 13. Що називається силовим полем? 14. Яке силове поле є стаціонарним? 15. Яке силове поле називається потенціальним? 16. За якою формулою визначається елементарна робота сили потенціального поля? 17. Чому дорівнює робота сили потенціального поля на кінцевому переміщенні точки? 18. Яка механічна система називається консервативною? 19. Сформулюйте закон збереження механічної енергії. Розділ Принципи механіки. Тема 6. Принцип Д`Аламбера (умовного зрівноваження сил). Література [1] §106-111 [2] Гл.5 §1,2 Термінологія «Принцип умовного зрівноваження сил» відображує сутність цього принципу. Його найчастіше називають принципом Д`Аламбера, хоча вірніше його треба б було назвати принципом Германа-Ейлера- Д`Аламбера, бо петербурзькі академіки Я.Герман (1716), Л.Ейлер (1737) встановили цей принцип. В 1743 р. Французький вчений Д`Аламбер вказав метод, за допомогою якого розв'язування задач динаміки зводилось до розв'язування задач методом статики, називають ще методом “Кінетостатики”. §6.1. Принцип Д`Аламбера для матеріальної точки.
Позначимо вектор Означення. Сила інерції зумовлена прискореним рухом матеріальної точки дорівнює добуткові маси точки на її прискорення і спрямована протилежно вектору прискорення.
Принцип Д`аламбера для точки: В кожний момент часу геометрична сума активних сил, реакцій в’язей, що діють на рухому матеріальну точку та умовно прикладеної до точки сили інерції дорівнює нулеві. §6.2. Принцип Д`Аламбера для механічної системи
к=1,2..n
Помножимо кожен із рядків (6.3) на радіус-вектор кожної точки відносно якогось нерухомого центру - т. О.
Що це за величина
Згадаємо, що геометрична сума сил – це головний вектор сил, а геометрична сума моментів сил відносно довільного центру – це головний момент сил відносно цього ж центру. Тоді (6.5), (6.7) математично виражають принцип Д`Аламбера для механічної системи. Принцип Д`Аламбера для системи. В кожний момент часу головний вектор і головний момент відносно деякого нерухомого центра всіх активних сил, реакцій вязей і умовно прикладених до точок механічної системи сил інерції, відповідно дорівнюють нулеві. Як відомо, сили які діють на систему можна класифікувати як активні і реакції в’язей, або зовнішні і внутрішні (Рис. 6.2). Маємо ще одну форму запису принципа Д`Аламбера для механічної системи.
Ці векторні рівняння можна спроєціювати на осі координат. Будемо мати рівняння “рівноваги”. Рівновага в лапках, бо насправді система рухається! Кількість рівнянь залежить від того, яку систему сил маємо: просторову чи плоску, довільну, збіжну чи паралельну. §6.3. Головний вектор і головний момент сил інерції.
  та теоремою про зміну кількості руху М.С. формула (3.4) та теоремою про зміну кількості руху М.С. формула (3.4)  . Маємо: . Маємо:
Головний вектор сил інерції механічної системи дорівнює взятій с протилежним знаком похідній від кількості руху цієї механічної системи, або, взятому з протилежним знаком, добутку маси системи на прискорення центру мас. Аналогічно, виходячи з (6.8) та теореми про зміну кінетичного моменту відносно центру т.О (формула (4.8)) отримаємо головний момент сил інерції відносно центру
§6.4. Головні вектори та головні моменти Д’Аламберових сил інерції твердих тіл. (законспектувати самостійно). Результати зведення Д’Аламберових сил інерції точок твердого тіла до простішого вигляду (метод Пуансо) маємо такі: 1. Поступальний рух тіла.
2. Тіло, яке має площину симетрії, обертається навколо нерухомої осі, яка перпендикулярна площині симетрії.
3. Плоский рух тіла.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 501; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


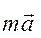




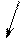





 Розглянемо рух невільної матеріальної точки масою m. Звільнимо її від в’язей і позначемо:
Розглянемо рух невільної матеріальної точки масою m. Звільнимо її від в’язей і позначемо:  рівнодійна активних сил, що діють на точку,
рівнодійна активних сил, що діють на точку,  рівнодійна реакцій в’язей.
рівнодійна реакцій в’язей. Запишемо основний закон динаміки точки
Запишемо основний закон динаміки точки 

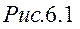 Побудуємо вектор
Побудуємо вектор  як суму векторів
як суму векторів 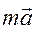 в праву частину, тобто
в праву частину, тобто 
 - сила інерції точки.
- сила інерції точки.
 Тепер (6.11) має вигляд
Тепер (6.11) має вигляд
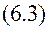 Розглянемо механічну систему, що здійснює деякий рух. Для кожної точки системи має місце рівняння (6.2)
Розглянемо механічну систему, що здійснює деякий рух. Для кожної точки системи має місце рівняння (6.2) рівнодійні активних сил і реакцій в’язей, що діють на “к”-ту точку, відповідно.
рівнодійні активних сил і реакцій в’язей, що діють на “к”-ту точку, відповідно.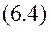


 Додамо “n” рядків (6.3):
Додамо “n” рядків (6.3): 
























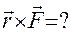 . Відповідь: це момент сили відносно точки О
. Відповідь: це момент сили відносно точки О

 Додамо “n” – рядків (6.6), враховуючи (*). Маємо:
Додамо “n” – рядків (6.6), враховуючи (*). Маємо:



 або
або 
 Головний вектор сил інерції можна визначити не тільки як геометричну суму сил інерції точок системи, а скориставшись рівнянням (6.8)
Головний вектор сил інерції можна визначити не тільки як геометричну суму сил інерції точок системи, а скориставшись рівнянням (6.8)





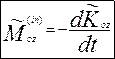
 Часто треба знати головний момент сил інерції відносно осі. Для цього треба спроєціювати (6.10) на вісь, наприклад Oz
Часто треба знати головний момент сил інерції відносно осі. Для цього треба спроєціювати (6.10) на вісь, наприклад Oz






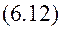

 М – маса тіла.
М – маса тіла.


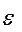



















 Якщо вісь обертання центральна, тоді:
Якщо вісь обертання центральна, тоді:













 Тіло, що має площину симетрії і рухається паралельно цій площині.
Тіло, що має площину симетрії і рухається паралельно цій площині.


