
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механічний принцип відносності(принцип відносності Галілея).Содержание книги
Поиск на нашем сайте
Розглянемо дві системи відліку: 1. Інерціальну систему 2. Систему Вважаємо, що в початковий момент часу, початки систем
Швидкість В проекціях на осі координат вектору рівність (1) подамо у вигляді співвідношень, що називається перетвореннями координат Галілея, тобто В класичній механіці приймають, що хід часу не залежать від відносного руху систем відліку, тому систему рівнянь (2) необхідно доповнити ще одним співвідношенням, а саме Продиференціюємо рівняння (1) по часу і враховуючи, що
Якщо на точку М діють інші тіла, то В загальному випадку сили взаємодії між тілами залежать від взаємного розміщення цих тіл і від швидкостей їх рух одне відносно одного. Тому сили, що діють на одну матеріальну точку з боку інших тіл однакові у всіх інерціальних системах відліку, тобто Із співвідношень (3) і (4) для ІСВ слідує, що
Отже, рівняння Ньютона для матеріальної точки, а також для довільних систем матеріальної точки мають однаковий вигляд у всіх інерціальних системах відліку. Іншими словами, інваріанти по відношенню до перетворень Галілея. Цей результат називається механічним принципом відносності (принципом відносності Галілея) і часто формулюється так: рівномірний прямолінійний рух(відносно будь-якої інерціальної системи відносності в замкнутій системі) не впливає на закономірності перебігу в ній механічних процесів і явищ, за однакових початкових умов. Або: ніякими механічними дослідами, проведеними в ІСВ не можна виявити, рухається вона рівномірно прямолінійно чи перебуває в стані спокою.
Розділ 3. Робота, енергія, закон збереження енергії. Механічна робота.
Механічна робота – скалярна фізична величина, що характеризує процес перетворення однієї форми руху в іншу і чисельно дорівнює скалярному добутку сили на переміщення
Формули (1) і (2) справедливі, якщо сила постійна по величині. Побудуємо графік, відкладаючи по осі Х пройдений тілом шлях, а по осі У – проекцію рухомої сили на напрям руху, тобто
В цьому випадку робота миттєвого значення сили на нескінченно малому шляху
А вся робота
Скористаємося (4) для обчислення роботи, яку здійснює сила тяжіння при русі тіла. Розглянемо наприклад, рух тіла масою
Проекція цієї сили на напрям переміщення АВ дорівнює
Величина проекції сили
Звідси слідує, що робота сили тяжіння не залежить від довжини шляху по похилій площині, а залежить тільки від висоти, на яку спустилося тіло, тобто, тільки від початкового та кінцевого положення тіла. Аналогічною властивістю володіє сила пружності. Проаналізуємо більш детально формулу (2): 1) 2) 3) Приклади:
А=0 2. Електричний заряд рухається вздовж еквіпотенціальної поверхні(тобто поверхні з однаковими потенціальними Це також слідує із формули електродинаміки
3. Заряджена частинка рухається в однорідному магнітному полі, на неї діє сила Лоренца, яка за своїм походженням є доцентровою силою.
Отже, сила Лоренца роботи не виконує
4) Приклади:
2. Пружина не навантажена. Сила пружності дорівнює нулю.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.176.238 (0.007 с.) |

 , яку умовно вважатимемо нерухомою.
, яку умовно вважатимемо нерухомою. - швидкість якої в поступальному русі
- швидкість якої в поступальному русі 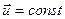 , тобто рухається рівномірно і прямолінійно відносно систем (1).
, тобто рухається рівномірно і прямолінійно відносно систем (1).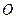 і
і  співпадають. Тоді взаємне розміщення цих систем в довільний момент часу t має вигляд, зображений на мал. 1.
співпадають. Тоді взаємне розміщення цих систем в довільний момент часу t має вигляд, зображений на мал. 1.

 направлена вздовж прямої
направлена вздовж прямої 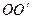 , а
, а  ,тоді положення довільної точки М в нерухомій і рухомій системах відліку визначається радіус-векторами
,тоді положення довільної точки М в нерухомій і рухомій системах відліку визначається радіус-векторами  і
і  , причому
, причому  (1)
(1) (2)
(2) (2а).
(2а). =>
=> 

 (3)
(3) . Але і
. Але і  , тоді дана рухома система
, тоді дана рухома система  (4).
(4).
 (1)
(1) (2)
(2) .
. Якщо під час руху величини
Якщо під час руху величини  В границі при нескінченно малих довжинах ділянок шляху робота змінної сили буде чисельно дорівнювати площі фігури на графіку.
В границі при нескінченно малих довжинах ділянок шляху робота змінної сили буде чисельно дорівнювати площі фігури на графіку.
 (3)
(3) (4)
(4) по похилій площині з кутом нахилу
по похилій площині з кутом нахилу  .(мал.3)
.(мал.3) На тіло діє сила тяжіння, під дією якої тіло рухається по похилій площині (тертям нехтуємо).
На тіло діє сила тяжіння, під дією якої тіло рухається по похилій площині (тертям нехтуємо).
 . На переміщення АВ сила
. На переміщення АВ сила 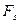 здійснить роботу
здійснить роботу
 де
де  =
=  - висота, на яку спустилося тіло.
- висота, на яку спустилося тіло. ,
, 
 ,
, 
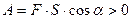
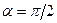 ,
, 

 1. Штучний супутник Землі рухається по кривій орбіті.
1. Штучний супутник Землі рухається по кривій орбіті.
 ), в кожній точці якої вектор сили і вектор переміщення складають кут
), в кожній точці якої вектор сили і вектор переміщення складають кут  , тобто робота не виконується.
, тобто робота не виконується.

 Тобто в кожній точці траєкторії вона складає кут
Тобто в кожній точці траєкторії вона складає кут  з напрямом переміщення.
з напрямом переміщення.



 1.
1.







