
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон збереження момента імпульса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
У випадку, якщо сумарний момент зовнішніх сил, що діють на тіло чи систему тіл, дорівнює нулю(
Отже, якщо сума моментів зовнішніх сил дорівнює нулю, то момент імпульсу системи не змінюється з часом. В цьому полягає закон збереження моменту імпульсу. Знайдемо вираз для кінетичної енергії тіла, що обертається. Кінетична енергія тіла, що обертається, дорівнює сумі кінетичних енергій його частинок
Виразимо кінетичну енергію тіла, що обертається, через момент імпульсу.
Розділ 5. Рівняння руху.
Узагальнені координати.
Для визначення положення системи в Взагалі число незалежних величин, завдання яких необхідне для однозначного визначення положення системи, називається числом її ступенів вільності, в даному випадку це число дорівнює 3 Завдання значень узагальнених координат, це не визначає „механічного стану” системи в даний момент часу, бо не дозволяє передбачити положення системи в наступні моменти часу. При заданих значеннях координат система може мати довільні швидкості, а в залежності від значення останніх буде різним і положення системи в наступний момент часу(тобто через нескінченно малий часовий інтервал Одночасне завдання всіх координат і швидкостей повністю визначається, як показує дослід, стан системи і дозволяє в принципі передбачати подальший її рух. З математичної точки зору це означає, що заданням всіх координат
Співвідношення, що пов’язують прискорення з координатами і швидкостями, називається рівнянням руху. По відношення до функцій
Принцип найменшої дії.
Найбільш загальне формування закону руху механічних систем дається так званим принципом найменшої дії (або принципом Гамільтона). Згідно з цим принципом кожна механічна система характеризується певною функцією
Нехай в моменти часу
мав найменше можливе значення. Функція Для спрощення запису формул спочатку припустимо, що система має всього одну ступінь вільності, так що повинна бути визначена всього одна функція Нехай
де Так як при
Зміна
Розклад цієї різниці по степеням
або виконавши варіювання
Відмітивши, що
Але враховуючи умови (3) перший член в цьому виразі зникає. Залишається інтеграл, який повинен дорівнювати нулю при довільних значеннях
При наявності кількох ступенів вільності в принципі найменшої дії повинні залежно варіюватися
Це шукані диференціальні рівняння; вони називаються в механіці рівняннями Лагранжа. Якщо функція Лагранжа, даної механічної системи відома, то рівняння (6) встановлюють зв’язок між прискореннями, швидкостями і координатами, тобто вони є рівняннями руху системи. Зазначимо, що функція Лагранжа визначена лише з точністю до додавання до неї повної похідної від довільної функції координат і часу.
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.3.102 (0.011 с.) |

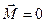 ), тоді
), тоді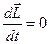 або
або 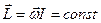 (1)
(1)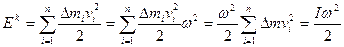 (2)
(2)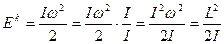 (3)
(3) На практиці часто зустрічаються випадки, коли тіло одночасно має і кінетичну енергію поступального руху і кінетичну енергію обертального руху, наприклад, куля скочується з похилої площини.
На практиці часто зустрічаються випадки, коли тіло одночасно має і кінетичну енергію поступального руху і кінетичну енергію обертального руху, наприклад, куля скочується з похилої площини.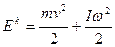
 матеріальних точок, в просторі треба задати
матеріальних точок, в просторі треба задати  величин
величин 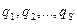 , що повністю характеризують положення системи(з
, що повністю характеризують положення системи(з 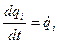 - її узагальненими швидкостями.
- її узагальненими швидкостями.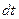 ).
).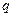 і швидкостей
і швидкостей 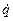 в деякий момент часу одночасно визначається також і значення прискорень
в деякий момент часу одночасно визначається також і значення прискорень 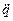 в цей момент(Надалі ми будемо умовно розуміти під
в цей момент(Надалі ми будемо умовно розуміти під 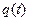 це – диференціальне рівняння другого порядку, інтегрування яких дозволяє в принципі визначати ці функції, тобто траєкторії руху механічної системи.
це – диференціальне рівняння другого порядку, інтегрування яких дозволяє в принципі визначати ці функції, тобто траєкторії руху механічної системи.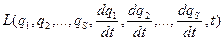 , або в скороченому записі
, або в скороченому записі 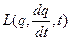 , причому рух системи задовольняє такій умові:
, причому рух системи задовольняє такій умові: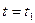 і
і 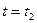 система певні положення, що характеризуються двома наборами значень координат
система певні положення, що характеризуються двома наборами значень координат 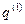 і
і 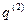 . Тоді між цими положеннями система рухається таким чином, щоб інтеграл
. Тоді між цими положеннями система рухається таким чином, щоб інтеграл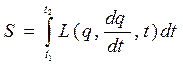 (1)
(1) називається функцією Лагранжа даної системи, а інтеграл (1) – дією.
називається функцією Лагранжа даної системи, а інтеграл (1) – дією.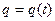 і є функція, для якої
і є функція, для якої 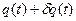 , (2)
, (2)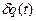 - функція, мала на всьому інтервалі часу від
- функція, мала на всьому інтервалі часу від 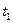 до
до 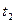 (її називають варіацією функції
(її називають варіацією функції 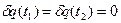 (3)
(3)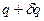 дається різницею:
дається різницею: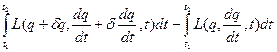
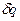 і
і 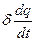 (в підінтегральному виразі) починається з членів першого порядку. Необхідною умовою мінімальності
(в підінтегральному виразі) починається з членів першого порядку. Необхідною умовою мінімальності 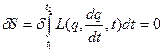 (4)
(4)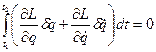
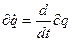 , про інтегруємо другий член по частинам і отримаємо:
, про інтегруємо другий член по частинам і отримаємо: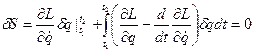 (5)
(5)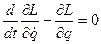
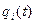 . Очевидно, що ми отримуємо тоді
. Очевидно, що ми отримуємо тоді 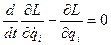 (і=1,2,...,
(і=1,2,..., 


