
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наслідки з основного рівняння кінетичної теорії ідеального газу.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
а) Закон Бойля – Маріотта Скористаємося рівнянням Клаузіуса у вигляді:
Врахувавши, що Закон Бойля – Маріотта описує ізотермічний процес, тобто процес, що протікає при постійний температурі По друге, закон Бойля – Маріотта має місце для газу, кількість молекул якого незмінна, тобто Тоді Добуток тиску газу на об’єм при даній масі газу і при постійній температурі є величина постійна. Виникає питання: в чому полягає фізичний зміст закону Бойля – Маріотта? Для відповіді на поставлене питання перевіримо розмірність цього закону в СІ.
Отже, з точки зору фізики закон Бойля – Маріотта показує, що при ізотермічному процесі внутрішня енергія газу не змінюється. б) Середня кінетична енергія поступального руху молекули ідеального газу. Скористаємося основним рівнянням Клаузіуса в формі:
Для молярного об’єму кількість молекул дорівнює числу Авогадро
Запишемо рівняння Клапейрона – Менделєєва для 1 моля газу:
Співставивши (1) і (2), отримаємо:
Отже, З (3) слідує фізичний зміст постійної Больцмана: вона показує, яку роботу здійснює 1 молекула газу, що рухається з деякою середньою швидкістю, при підвищені температури газу на 1 0К. в) Число Лошмідта Підрахуємо кількість молекул газу в одиницю об’єму. Для цього скористаємося основним рівнянням МКТ, що має вигляд:
Підставляючи сюди значення
Тоді При однакових температурі і тиску всі газу містять в одиниці об’єму однакову кількість молекул. Кількість молекул, що міститься в 1 м3 газу за нормальних умов називається числом Лошмідта. За формулою (5) воно дорівнює
г) Середня квадратична швидкість руху молекул ідеального газу: Виводячи основне рівняння МКТ ми позначимо середню квадратичну швидкість через
Тоді
тобто для даного газу середня квадратична швидкість молекул пропорційна кореню квадратному з абсолютної температури і залежить тільки від неї.
§4. Розподіл числа молекул за швидкостями(розподіл Максвела).
Серед квадратична швидкість – менше статистична характеристика руху молекул, отримана шляхом усереднення різних значень швидкостей значної кількості молекул. В дійсності ж молекули рухаються з різними швидкостями Розіб’ємо весь діапазон цих швидкостей на малі інтервали
Цю функцію розподілу вперше визначив англ. фізик Джеймс Клерк Максвелл теоретичним шляхом, застосувавши теорію ймовірностей. Максвелівська функція розподілу представлена формулою, яка називається законом Максвела і має такий вид:
де
При Знайдемо найбільш ймовірну швидкість, при якій функція розподілу має максимум. Для цього першу похідну функції розподілу по
Найбільш ймовірною називається швидкість, поблизу якої на одиничний інтервал припадає найбільша кількість молекул. Вона розраховується за формулою (2). Графічно закон Максвела представлено кривою, що починається в початку координат, досягає максимуму при
Графік точно показує, що молекул з малими і великими швидкостями мало і що більшість молекул має швидкості, близькі до найбільш ймовірної швидкості. Із закону Максвелла можна отримати вираз для середньої арифметичної швидкості Вона дорівнює
Ці вирази показують, що дані швидкості розрізняються між собою тільки коефіцієнтами:
Виділимо на осі абсцис елементарний інтервал швидкостей
тобто числу молекул, що мають швидкість в інтервалі При зміні температури газу змінюються швидкості руху всіх молекул, а отже і найбільш ймовірна швидкість. Тому максимум кривої буде зміщуватись вправо, при підвищені температури, або вліво при зниженні температури, однак площа, обмежена кривою, залишається незмінною, бо загальна кількість молекул газу не залежить від температури. Розподіл Максвелла за швидкостями був підтверджений експериментально німецьким фізиком Штерном у 1920 р.
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.25.100 (0.008 с.) |


 , тому отримаємо
, тому отримаємо  =>
=> 
 , тоді
, тоді  .
.
 - закон Бойля – Маріотта.
- закон Бойля – Маріотта.
 , де
, де  - молярний об’єм
- молярний об’єм

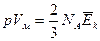 (1)
(1) (2)
(2) =>
=> 
 - постійна Больцмана
- постійна Больцмана (3)
(3) з формули (3), отримаємо:
з формули (3), отримаємо:
 (4)
(4) (5)
(5)
 . Тоді середня кінетична енергія
. Тоді середня кінетична енергія . З іншого боку
. З іншого боку  =>
=> 
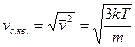


 =>
=> 
 (6)
(6) навіть при деякий заданій температурі
навіть при деякий заданій температурі 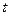 .
. . Тоді на кожний інтервал швидкості буде припадати деяке число молекул
. Тоді на кожний інтервал швидкості буде припадати деяке число молекул  , що мають швидкість, обмежену цим інтервалом. Відношення
, що мають швидкість, обмежену цим інтервалом. Відношення 
 показує, скільки молекул припадає на кожний одиничний інтервал швидкості. Іншими словами, який розподіл числа молекул за швидкостями.
показує, скільки молекул припадає на кожний одиничний інтервал швидкості. Іншими словами, який розподіл числа молекул за швидкостями. (1)
(1) - загальна кількість молекул газу
- загальна кількість молекул газу - молярна маса
- молярна маса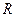 - універсальна газова постійна
- універсальна газова постійна і при
і при  функція розподілу прагне до нуля.
функція розподілу прагне до нуля. прирівняємо до нуля.
прирівняємо до нуля.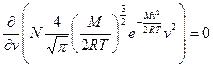


 при
при 
 (2)
(2) і потім асимптотично наближається до осі абсцис(мал.1).
і потім асимптотично наближається до осі абсцис(мал.1).



 .
.

 ,
,


