
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однорідні диференціальні рівняння першого порядкуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Наприклад, функція
Поділимо обидві частини рівняння на
Перевіримо рівність (1.8
Використаємо підстановку (1.9 Підставимо вирази Зведемо подібні доданки Отримаємо диференціальне рівняння з відокремлюваними змінними:
За формулами №13 і №4 таблиці невизначених інтегралів отримаємо:
Перейдемо до змінних
Розв'яжемо задачу Коші, використавши початкову умову: Для спрощення перетворень підставимо значення
Відповідь.
Перевіримо рівність (1.8
Рівність (1.8 Використаємо підстановку (1.9 Підставимо вирази
Поділивши обидві частини рівняння на
Замінимо в даному рівнянні
(поділимо обидві частини рівняння на
Для знаходження інтеграла
Перейдемо до змінних
Відповідь.
Маємо рівняння в диференціальній формі (1.3), в якому
тому Аналогічно можна довести, що функція Для отримання виразу
Використаємо підстановку (1.9 рівняння:
Замінимо в даному рівнянні
За формулами №17 і №4 таблиці невизначених інтегралів отримаємо:
Перейдемо до змінних
Відповідь. 1.4. Диференціальні рівняння, які зводяться до однорідних диференціальних рівнянь
Маємо диф. рівняння виду (1.10), в якому
Із першого рівняння системи: Здійснимо підстановку за формулами (1.11):
Виразимо із підстановки:
Дане диф. рівняння розв'язане (приклад, стр. 16, 17). Загальний інтеграл рівняння має вигляд:
Використавши підстановку
Відповідь.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 776; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.187.224 (0.011 с.) |

 Функція
Функція  називається однорідною функцією
називається однорідною функцією  го виміру відносно змінних
го виміру відносно змінних  та
та  , якщо для довільного
, якщо для довільного  виконується рівність:
виконується рівність:

 є однорідною функцією
є однорідною функцією  го виміру, бо
го виміру, бо 

 Функція
Функція  го виміру відносно змінних
го виміру відносно змінних 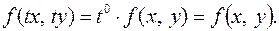
 )
)


 Також однорідними функціями
Також однорідними функціями  Наприклад:
Наприклад: 
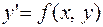
 го порядку, якщо функція
го порядку, якщо функція 
 невідома функція.
невідома функція. Розв'язати диф. рівняння:
Розв'язати диф. рівняння: 
 Розв'язання.
Розв'язання. , який є однорідною функцією
, який є однорідною функцією 
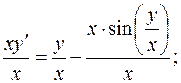
 тобто
тобто 
 не можна записати у вигляді (1.5)
не можна записати у вигляді (1.5)  тому дане рівняння не є диференціальним рівнянням з ві-докремлюваними змінними.
тому дане рівняння не є диференціальним рівнянням з ві-докремлюваними змінними.
 Рівність (1.8
Рівність (1.8  є однорідною функцією
є однорідною функцією  Диференціюємо вираз підстановки
Диференціюємо вираз підстановки  по змінній
по змінній 


 у задане диф. рівняння
у задане диф. рівняння 

 в обох частинах рівняння і поділимо їх на
в обох частинах рівняння і поділимо їх на 
 Замінимо в даному рівнянні
Замінимо в даному рівнянні 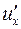 на
на 
 (домножимо обидві частини рівняння на
(домножимо обидві частини рівняння на  )
) (поділимо обидві частини рівняння на
(поділимо обидві частини рівняння на  )
)
 де
де  довільна стала.
довільна стала. , де
, де 
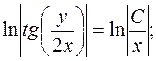 звідки
звідки 

 загальний розв'язок диф. рівняння.
загальний розв'язок диф. рівняння.
 не в загаль-ний розв'язок, а у вираз
не в загаль-ний розв'язок, а у вираз 
 звідки
звідки 


 не можна записати у вигляді (1.5)
не можна записати у вигляді (1.5) 
 є однорідною функцією
є однорідною функцією 




 отримаємо диференціальне рівняння з відокремлюваними змінними:
отримаємо диференціальне рівняння з відокремлюваними змінними:
 (домножимо обидві частини рівняння на
(домножимо обидві частини рівняння на 
 )
)
 де
де 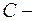 довільна стала.
довільна стала. використаємо метод заміни змінної (таблиця 2):
використаємо метод заміни змінної (таблиця 2):
 де
де  (домножимо обидві частини на
(домножимо обидві частини на  )
)
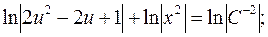
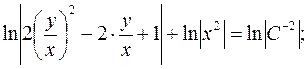

 загальний інтеграл диф. рівняння.
загальний інтеграл диф. рівняння. де
де 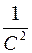 можна замінити на
можна замінити на  де
де 

 і
і  є однорідними функціями одного й того самого виміру.
є однорідними функціями одного й того самого виміру.




 однорідна функція
однорідна функція  однорідна функція
однорідна функція  поділимо обидві частини рівняння на
поділимо обидві частини рівняння на 

 (поділимо на
(поділимо на 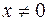 )
)


 Зведемо подібні доданки
Зведемо подібні доданки 
 (поділимо обидві частини рівняння на
(поділимо обидві частини рівняння на  диф. рівняння з відокремлюваними змінними.
диф. рівняння з відокремлюваними змінними.



 де
де  ;
;


 (домножимо на
(домножимо на  загальний інтеграл.
загальний інтеграл.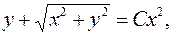 де
де 
 задані числа.
задані числа.
 ,
,
 єдиний розв'язок системи рівнянь
єдиний розв'язок системи рівнянь  рівняння (1.10) зводиться до однорідного диф. рівняння (1.9).
рівняння (1.10) зводиться до однорідного диф. рівняння (1.9). тоді, використовуючи заміну
тоді, використовуючи заміну


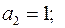
 .
. розв'яжемо систему рівнянь:
розв'яжемо систему рівнянь: Віднімемо почленно від першого рівняння системи друге.
Віднімемо почленно від першого рівняння системи друге.

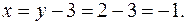

 і підставимо у задане рівняння:
і підставимо у задане рівняння: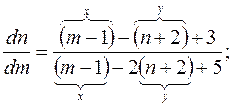
 однорідне диф.рівняння.
однорідне диф.рівняння. де
де  отримаємо загальний інтеграл заданого рівняння:
отримаємо загальний інтеграл заданого рівняння: де
де 


