
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальні поняття. Задача Коші.Содержание книги
Поиск на нашем сайте
Рівняння (1.1) може не містити явно незалежну змінну
Отримали диференціальне рівняння у нормальній формі (1.2), в якому Як відомо,
Отримане рівняння є диференціальним рівнянням першого порядку у диференціальній формі (1.3). У загальному випадку:
різних розв'язків виду на стала. Графіками цих розв'язків є множина інтегральних кривих, які утворюються у відкритій області
Нехай диференціальне рівняння (1.2) задовольняє в області
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 Диференціальним рівнянням першого порядку називається рівняння виду:
Диференціальним рівнянням першого порядку називається рівняння виду:

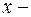 незалежна змінна,
незалежна змінна, 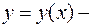 невідома функція.
невідома функція. або невідому функцію
або невідому функцію  але обов'язково має містити похідну
але обов'язково має містити похідну  невідомої функції.
невідомої функції. або
або 

 Диференціальне рівняння
Диференціальне рівняння  є неявним диференціальним рівнянням першого порядку (1.1), але в ньому можна виразити похідну
є неявним диференціальним рівнянням першого порядку (1.1), але в ньому можна виразити похідну 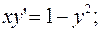
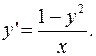
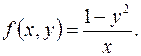
 тоді, замінивши у лівій частині останнього рівняння
тоді, замінивши у лівій частині останнього рівняння  отримаємо:
отримаємо:




 і
і  відомі функції, називають диференціальним рівнян-ням першого порядку у диференціальній формі.
відомі функції, називають диференціальним рівнян-ням першого порядку у диференціальній формі. Очевидно, що не кожне диференціальне рівняння першого порядку можна записати у нормальній (1.2) та диференціальній (1.3) формах. Надалі будемо розглядати диференціальні рівняння виду (1.2), у яких можна виразити похідну
Очевидно, що не кожне диференціальне рівняння першого порядку можна записати у нормальній (1.2) та диференціальній (1.3) формах. Надалі будемо розглядати диференціальні рівняння виду (1.2), у яких можна виразити похідну  Нехай у диференціальному рівнянні (1.2) функція
Нехай у диференціальному рівнянні (1.2) функція  і її частинна похідна
і її частинна похідна  визначені і неперервні у відкритій області
визначені і неперервні у відкритій області  площини
площини  і точка
і точка 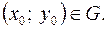 Тоді існує єдиний розв'язок
Тоді існує єдиний розв'язок  рівняння (1.2), який задовольняє умову:
рівняння (1.2), який задовольняє умову:
 або
або  .
.
 , де
, де  деяка функція,
деяка функція, 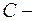 довіль-
довіль- по осі
по осі  на довільне число
на довільне число 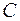 (рис. 1). Тоді, геометрично, теорема Коші стверджує, що через кожну точку
(рис. 1). Тоді, геометрично, теорема Коші стверджує, що через кожну точку  проходить єдина інтегральна крива
проходить єдина інтегральна крива  (рис. 1).
(рис. 1).
 при
при  на-зивають початковою умовою розв'язку і записують у вигляді:
на-зивають початковою умовою розв'язку і записують у вигляді:
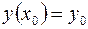
 )
)
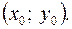
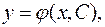 де
де 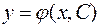 є розв'язком диф. рівняння при будь-якому значенні сталої
є розв'язком диф. рівняння при будь-якому значенні сталої  можна знайти таке значення
можна знайти таке значення  , що функція
, що функція 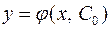 задовольняє початкову умову
задовольняє початкову умову  .
.
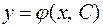 при певному значенні
при певному значенні 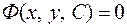 називають загальним інтегралом диференціального рівняння. Частинний розв'язок, знайдений у неявній формі
називають загальним інтегралом диференціального рівняння. Частинний розв'язок, знайдений у неявній формі  називають частиннимінтегралом диференціального рівняння.
називають частиннимінтегралом диференціального рівняння.
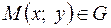 диференціальне рівняння (1.2) ставить у відповідність значення кута
диференціальне рівняння (1.2) ставить у відповідність значення кута  тобто рівняння (1.2) геометрично задає поле напрямів (зазвичай, поле напрямів зображують стрілками). А розв'язок диференціального рівняння (1.2) задає інтегральну криву, яка в кожній власній точці "дотикається" до поля напрямів. Знаючи поле напрямів диф. рівняння, можна наближено побудувати його інтегральні криві. Для полегшення побудови поля напрямів використовують ізокліни.
тобто рівняння (1.2) геометрично задає поле напрямів (зазвичай, поле напрямів зображують стрілками). А розв'язок диференціального рівняння (1.2) задає інтегральну криву, яка в кожній власній точці "дотикається" до поля напрямів. Знаючи поле напрямів диф. рівняння, можна наближено побудувати його інтегральні криві. Для полегшення побудови поля напрямів використовують ізокліни. в кожній точці якої дотичні до інтегральних кривих мають один напрям.
в кожній точці якої дотичні до інтегральних кривих мають один напрям.


