
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференціальні рівняння у повних диференціалахСодержание книги
Поиск на нашем сайте
При розв'язуванні диф. рівняння (1.17) спочатку перевіряють умову (1.20), при виконанні якої дане рівняння є диф. рівнянням у повних диференціалах. Тобто невідома функція
де
У заданому рівнянні
Перевіримо умову (1.20):
Умова (1.20) виконується, тому маємо диференціальне рівняння у повних диференціалах. Знайдемо функцію Згідно (1.18 Інтегруємо останню рівність по змінній
Для знаходження функції
Отже, Використовуючи рівність (1.19), отримаємо загальний інтеграл диф. рівняння: Відповідь.
1.8. Диференціальні рівняння n– го порядку
Якщо диференціальне рівняння не розв'язане відносно старшої похідної
Зокрема, для диференціального рівняння другого порядку
Існування і єдиність розв'язку задачі Коші для рівняння (1.23) обгрунтовує наступна теорема Коші.
Якщо функція
1.9. Диференціальні рівняння Розглянемо деякі класи диференціальних рівнянь
Інтегрується в квадратурах. Загальний розв'язок рівняння (1.27) знаходять за допомогою
|
 Розв'язати диференціальне рівняння:
Розв'язати диференціальне рівняння:

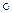 Розв'язання.
Розв'язання.

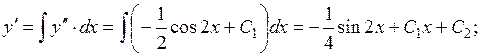

загальний розв’язок рівняння.
Значення довільних сталих  знайдемо, використовуючи задані початкові умови
знайдемо, використовуючи задані початкові умови 
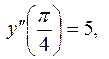 тоді, підставивши у першу рівність
тоді, підставивши у першу рівність  значення
значення  отримаємо:
отримаємо: 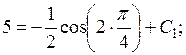
 звідки
звідки 
Врахувавши, що  отримаємо:
отримаємо: 
 тоді маємо рівняння:
тоді маємо рівняння:  звідки
звідки 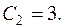
Врахувавши, що  отримаємо:
отримаємо: 
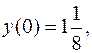 тоді, підставивши в останню рівність
тоді, підставивши в останню рівність  отримаємо:
отримаємо:
 звідки
звідки 
Відповідь.  частинний розв'язок.
частинний розв'язок. 
 Диференціальне рівняння виду Диференціальне рівняння виду 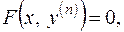 яке можна розв'язати відносно яке можна розв'язати відносно  : :
Інтегрується в квадратурах. Використовуючи заміну звідки
При цьому загальний розв'язок диф. рівняння (1.28) отримують у параметричній формі: |
 Розв'язати диференціальне рівняння:
Розв'язати диференціальне рівняння: 
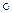 Розв'язання.
Розв'язання.
Записавши дане рівняння у вигляді  , отримаємо рівняння (1.28).
, отримаємо рівняння (1.28).
Нехай  , тоді останню рівність запишемо у вигляді:
, тоді останню рівність запишемо у вигляді:
 звідки
звідки 
Задано рівняння другого порядку, тобто  тоді, використовуючи залежність (1.28*), отримаємо:
тоді, використовуючи залежність (1.28*), отримаємо:


 Відповідь.
Відповідь. 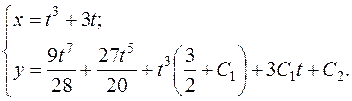

|
| Поделиться: |

 Диференціальне рівняння виду:
Диференціальне рівняння виду:

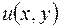 , тобто
, тобто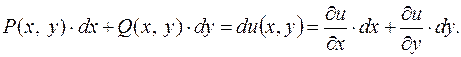

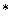 )
)

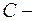 довільна стала інтегрування.
довільна стала інтегрування.
 задовольняє умови (1.18
задовольняє умови (1.18  по
по  визначають функцію
визначають функцію 

 первісна функції
первісна функції  по змінній
по змінній  константою. Диференціюючи останню рівність по
константою. Диференціюючи останню рівність по  отримують рівняння для знаходження функції
отримують рівняння для знаходження функції 
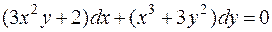 .
.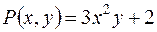 ,
, 
 Задане рівняння не є однорідним диф. рівнянням, бо, наприклад, функція
Задане рівняння не є однорідним диф. рівнянням, бо, наприклад, функція 



 використаємо другу умову (1.18
використаємо другу умову (1.18 
 звідки
звідки  звідки
звідки

 де
де 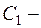 довільна стала;
довільна стала;

 де
де  яка називається інтегрувальним множником, так, що це рівняння стане диф. рівнянням у повних диференціалах.
Методи знаходження інтегрувальних множників
яка називається інтегрувальним множником, так, що це рівняння стане диф. рівнянням у повних диференціалах.
Методи знаходження інтегрувальних множників  у даному посібнику не розглядаються.
у даному посібнику не розглядаються.

 обчислюється при сталому значенні
обчислюється при сталому значенні 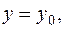 а другий визначений інтеграл
а другий визначений інтеграл  обчислюється при сталому значенні
обчислюється при сталому значенні  Початкову точку
Початкову точку  у формулі (1.21) вибирають так, щоб підінтегральні вирази були найпростішими.
у формулі (1.21) вибирають так, щоб підінтегральні вирази були найпростішими.
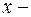 незалежна змінна,
незалежна змінна, 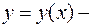 невідома функція,
невідома функція,  відома функція,
відома функція, го порядку.
го порядку. є обов'язковим виразом, а наявність в ньому інших виразів
є обов'язковим виразом, а наявність в ньому інших виразів  необов'язкова.
необов'язкова.
 називається
називається 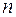 разів неперервно диференційовна на цьому інтервалі функція
разів неперервно диференційовна на цьому інтервалі функція  , яка при підстановці в дане рівняння перетворює його на тотожність відносно незалежної змінної
, яка при підстановці в дане рівняння перетворює його на тотожність відносно незалежної змінної 
 диференціального рівняння (1.22) або (1.23) називається інтегральною кривою даного диференціального рівняння.
диференціального рівняння (1.22) або (1.23) називається інтегральною кривою даного диференціального рівняння.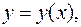
 який при
який при  задовольняє початкові умови:
задовольняє початкові умови:
 або
або
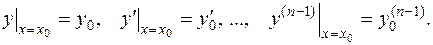
 початкові умови при
початкові умови при  мають вигляд:
мають вигляд:

 і її частинні похідні по аргументам
і її частинні похідні по аргументам 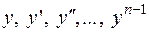 неперервні в даній відкритій області
неперервні в даній відкритій області  , то для кожної точки
, то для кожної точки  існує єдиний розв’язок
існує єдиний розв’язок  рівняння (1.23), який задовольняє початкові умови (1.24).
рівняння (1.23), який задовольняє початкові умови (1.24).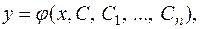
 довільні сталі інтегрування.
довільні сталі інтегрування.
 надати конкретного числового значення. Числові значення
надати конкретного числового значення. Числові значення 
 задана неперервна на деякому проміжку функція,
задана неперервна на деякому проміжку функція,
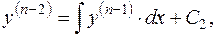 .........
.........


 отримаємо рівняння
отримаємо рівняння 
 . Після цього рівняння (1.28) розв'язують аналогічно до диференціального рівняння (1.27), інтегруючи
. Після цього рівняння (1.28) розв'язують аналогічно до диференціального рівняння (1.27), інтегруючи 




