
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Індивідуальні контрольні завданняСодержание книги
Поиск на нашем сайте
Завдання 1. Знайти частинні розв'язки або частинні інтеграли диференціальних рівнянь з відокремлюваними змінними: 1. 2. 3. 4.
5.
6. 7.
8. 9. 10. 11.
12.
13. 14.
15. 16. 17.
18. 19. 20.
21. 22. 23.
24.
25.
26.
27.
28. 29. 30. Завдання 2. Розв'язати диференціальні рівняння: 1. 2.
3. 4.
5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19.
20. 21. 22. 23.
24. 25. 26. 27. 28. 29. 30.
Завдання 3. Знайти частинні розв'язки лінійних однорідних диференціальних рівнянь: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. Завдання 4. Знайти загальні розв'язки лінійних неоднорідних диференціальних рівнянь: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. Завдання 5. Розв’язати нормальні системи диференціальних рівнянь методом виключення змінної: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30) ВІДПОВІДІ ДО КОНТРОЛЬНИХ ЗАВДАНЬ Відповіді до завдання 1. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
Відповіді до завдання 2. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
Відповіді до завдання 3. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.
Відповіді до завдання 4. ( 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. Відповіді до завдання 5. (
1.
2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26.
27. 28. 29. 30. ІМЕННИЙ ПОКАЖЧИК Абель Нільс Хенрік (1802–1829) – норвезький математик Бернуллі Йоган (1667–1748) – швейцарський математик Бернуллі Якоб (1654–1705) – швейцарський математик, родоначальник династії видатних учених математиків і механіків Вронський Юзеф (1776–1853) – польський математик Ейлер Леонард (1707–1783) – швейцарський математик, механік, фізик Коші Огюстен Луї (1789–1857) – французський математик Крамер Габриель (1704–1752) – швейцарський математик Лагранж Жозеф (1736–1813) – французський математик Ріккаті Джакопо Франческо (1676–1754) – італійський математик ПРЕДМЕТНИЙ ПОКАЖЧИК В изначник Вронського (вронскіан) – стр. 45; Д иференціальне рівняння – стр. 4; – Бернуллі – стр. 28; – в частинних похідних – стр. 4; – допускає пониження порядку – стр. 40; 41; – звичайне – стр. 4; – з відокремлюваними змінними – стр. 9; 11. – інтегрується в квадратурах – cтр. 8; – лінійне (першого порядку)– стр. 22; – лінійне ( – лінійне неоднорідне другого порядку із сталими коефіцієнтами – стр. 53; – лінійне однорідне другого порядку із сталими коефіцієнтами – стр. 50; – неявне (першого порядку)– стр. 5; – неявне ( – нерозв'язне відносно похідної (першого порядку) – стр. 5; – нормальне або явне ( – однорідне (першого порядку) – стр. 13; – першого порядку – стр. 5; – Ріккаті – стр. 28; – у повних диференціалах – стр. 39; – у нормальній формі (першого порядку)– стр. 5; – З агальний інтеграл диф. рівняння першого порядку – стр. 8; загальний розв'язок диф. рівняння першого порядку – стр. 8; задача Коші – стр.7;36; І зокліна – стр.8; інтегральна крива диференціального рівняння – стр. 4; 35; інтегрувальний множник – стр. 31; Л інійно залежні функції – стр.44; лінійно незалежні функції – стр.45; лінійне неоднорідне диф. рівняння – другого порядку – стр. 47; – другого порядку із сталими коефіцієнтами – стр. 53; лінійне однорідне диф. рівняння – другого порядку – стр. 44; – другого порядку із сталими коефіцієнтами – стр. 50; М етод Бернуллі інтегрування лінійного диф. рівняння стр. 23; – варіації довільних сталих (Лагранжа) – стр. 47; – виключення змінної – стр. 69; Н ормальна система диференціальних рівнянь – стр. 68; О днорідна функція – нульового виміру – стр. 13; особлива інтегральна крива – стр.7; – точка – стр.7; особливий розв'язок диференціального рівняння – стр.7; П оле напрямів – стр.8; порядок диференціального рівняння – стр. 4; початкова умова розв'язку – стр. 7; 36; Р озв'язок диференціального рівняння – стр. 4; 35; – загальний – стр.8; 36; – частинний – стр.8;36; С пеціальна права частина лінійного неоднорідного диф. рівняння другого порядку із сталими коефіцієнтам – стр. 53; Т еорема Коші (про існування і єдиність розв'язку диференціального рівняння першого порядку) – стр.6; – Коші (про існування і єдиність розв'язку диференціального рівняння – про накладання розв'язків – стр. 47; – про структуру загального розв’язку лінійного однорідного диф. рівняння другого порядку – стр. 45; – про структуру загального розв’язку лінійного неоднорідного диф. рівняння другого порядку – стр. 49;
Ф ормула Абеля – стр. 46; 66; Х арактеристичне рівняння – стр. 50; Ч астинний інтеграл диф. рівняння першого порядку – стр. 8; частинний розв'язок диф. рівняння першого порядку – стр. 8; ДОДАТКИ Таблиця 1. Диференціювання функцій
Таблиця 2.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.66.224 (0.01 с.) |

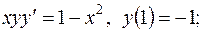

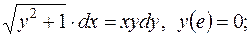


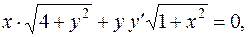










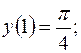


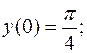



























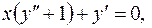


















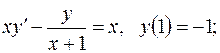




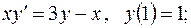













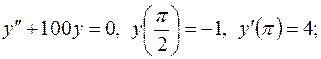






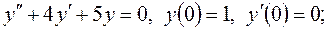



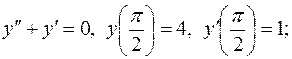













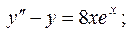

















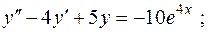

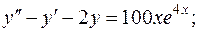



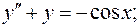
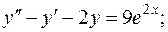
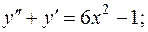
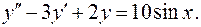




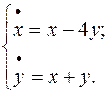

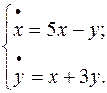




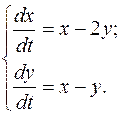
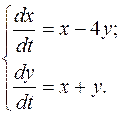














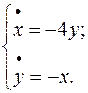






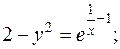
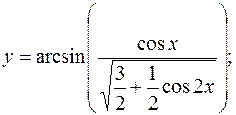



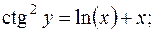
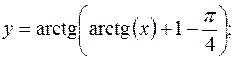











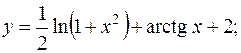


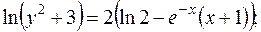

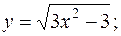






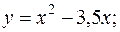




















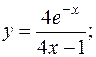







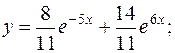

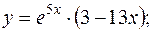



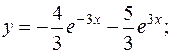
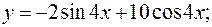
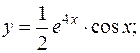

















 довільні сталі)
довільні сталі)













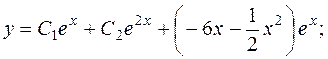

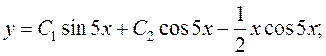

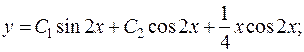












 Вирази із довільними сталими можуть відрізнятись від запропонованих (дивись зауваження на стор. 70).
Вирази із довільними сталими можуть відрізнятись від запропонованих (дивись зауваження на стор. 70).




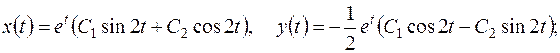













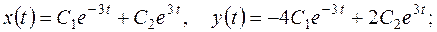




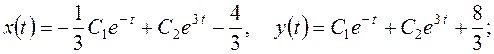








 порядку)– стр. 43; 66;
порядку)– стр. 43; 66; го порядку –
го порядку – 
 диференційовні в точці
диференційовні в точці  , тоді виконуються рівності:
, тоді виконуються рівності:

 де
де 
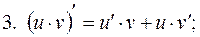
 5. Похідна складеної функції:
5. Похідна складеної функції:

 знаходять за формулою:
знаходять за формулою:

 де
де 

 де
де 

 де
де 

 де
де


















