
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтегрування нормальних систем методом виключенняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
У багатьох технічних задачах необхідно знайти кілька невідомих функцій, що пов’язані між собою диференціальними рівняннями, сукупність яких утворює систему диференціальних рівнянь.
У лівій частині даної системи диференціальних рівнянь знаходяться похідні першого порядку, а права частина – не містить похідних. Іноді позначають:
І навпаки, нормальну систему
Нормальну систему двох диференціальних рівнянь задають у вигляді:
де Зразок виконання контрольного завдання №5.
Знайдемо розв’язки системи
Диференціюємо друге рівняння системи
Підставимо в отриману рівність замість
Виразимо із другого рівняння системи
За теоремою (1.38) загальний розв'язок заданого рівняння дорівнює:
де
Розглянемо відповідне однорідне диф. рівняння:
За формулою (1.44) загальний розв'язок відповідного однорідного диф. рівняння дорівнює:
Спеціальна права частина заданого рівняння має вигляд (1.47):
Підставимо
поділимо обидві частини рівності на Тому Із другого рівняння системи виразимо:
Відповідь.
де
Виконуючи відповідні підстановки і перетворення, отримаємо відповідь:
де На перший погляд викликає сумнів у тотожності виразів довільних сталих біля функцій Переконатись у відповідності розв'язків системи диф. рівнянь при диференціюванні першого її рівняння із наведеними у зразку виконання (де спочатку диференціювали друге рівняння системи) можна, наприклад, позначивши:
Після цього перевіряють рівності:
Контрольні запитання 1. Дати означення диференціального рівняння, порядку, розв'язку диференціального рівняння, інтегральної кривої. 2. Визначити різні форми диференціального рівняння першого порядку. Сформулювати задачу Коші для диференціального рівняння першого порядку. Сформулювати означення загального і частинного розв'язку (та інтегралу) диференціального рівняння. 3. Що означає вислів "диференціальне рівняння інтегрується у квадратурах"? 4. Дати означення диференціального рівняння з відокремлюваними змінними та визначити особливості його розв'язування. 5. Яке диференціальне рівняння першого порядку називається однорідним? Яку підстановку треба використати для його розв'язування? 6. Які диференціальні рівняння зводяться до однорідного диференціального рівняння першого порядку? 7. У чому полягає метод Бернуллі розв'язування лінійного диференціального рівняння першого порядку? 8. Які диференціальні рівняння зводяться до лінійних першого порядку? 9. Яке диференціальне рівняння є рівнянням у повних диференціалах? Які особливості його розв'язування. 10. Сформулювати основні поняття і означення для диференціальних рівнянь вищих порядків. 11. Які диференціальні рівняння 12. Сформулювати теорему про структуру загального розв'язку лінійного однорідного та неоднорідного диференціального рівняння другого порядку?
13. У чому полягає метод варіації довільних сталих? 14. Записати формули розв'язків лінійного однорідного диференціального рівняння другого порядку із сталими коефіцієнтами. 15. Як розв'язувати лінійні неоднорідні диференціальні рівняння другого порядку із сталими коефіцієнтами та спеціальною правою частиною? 16. У чому полягає метод виключення змінної при розв'язуванні нормальних систем диференціальних рівнянь? Список рекомендованої літератури 1. Дубовик В.П. Вища математика: навч. посiбник / В.П. Дубовик, І.І. Юрик. – К.: Вища шк., 2004. – С. 421– 493. 2. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. – М.: Наука, 1982. – 576 с. 3. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. – М.: Наука, 1982. – 332 с. 4. Самойленко А.М. Диференціальні рівняння / А.М. Самойленко, М.О. Перестюк, І.О. Парасюк. – К.: Либідь, 1994. – 360 с. 5. Шестаков А.А. Курс высшей математики: Учеб. для студентов втузов / А.А. Шестаков, И.А. Малышева, Д.П. Полозков; под ред. А.А. Шеста-кова. – М.: Высш. шк., 1987. – С.125–230. 6. Шкіль М.І. Вища математика / М.І. Шкіль, Т.В. Колесник. – К: Вища шк., 1986. – С.183–299. 7. Шкіль М.І. Звичайні диференціальні рівняня / М.І. Шкіль, М.А. Сотни-ченко. – К: Вища шк., 1992. – 303 с. 8. Вища математика. Збірник задач: навч. посібник / [Дубовик В.П., Юрик І.І., Вовкодав І.П. та ін.]; за ред. В.П. Дубовика, І.І. Юрика. – К.: АСК, 2001. – 480с. 9. Гудименко Ф.С. Збірник задач з вищої математики: Учб. посібник для студентів природничих факультетів університетів / Ф.С. Гудименко, Д.М. Борисенко, В.О. Волкова та ін.; за ред. Ф.С. Гудименка. – К.: Вид-во Київського університету, 1967. – 352 с.
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 591; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.134.63 (0.01 с.) |

 Нормальною системою диференціальних рівнянь називається система виду:
Нормальною системою диференціальних рівнянь називається система виду:
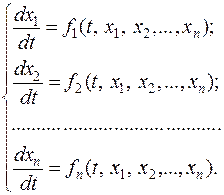
 .
. які задовольняють кожне з рівнянь системи.
які задовольняють кожне з рівнянь системи. До нормальної системи
До нормальної системи 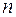 рівнянь першого порядку за допомогою введення нових змінних зводиться кожне диференціальне рівняння
рівнянь першого порядку за допомогою введення нових змінних зводиться кожне диференціальне рівняння  го порядку, розв’язане відносно старшої похідної.
го порядку, розв’язане відносно старшої похідної.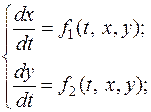 або
або 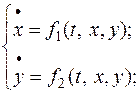
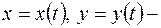 невідомі функції.
невідомі функції. Розв’язати нормальні системи диференціальних рівнянь методом виключення змінної:
Розв’язати нормальні системи диференціальних рівнянь методом виключення змінної: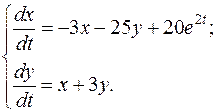
 Розв'язання.
Розв'язання.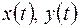 методом виключення змінної.
методом виключення змінної.
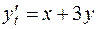 по змінній
по змінній 

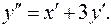
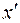 праву частину першого рівняння системи:
праву частину першого рівняння системи: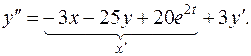
 і підставимо в останню рівність:
і підставимо в останню рівність: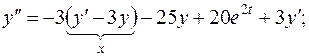

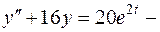 лінійне неоднорідне диф. рівняння другого порядку із сталими коефіцієнтами (1.46).
лінійне неоднорідне диф. рівняння другого порядку із сталими коефіцієнтами (1.46).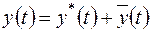 ,
,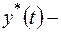 частинний розв’язок заданого диф. рівняння,
частинний розв’язок заданого диф. рівняння,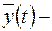 загальний розв’язок відповідного однорідного рівняння.
загальний розв’язок відповідного однорідного рівняння.
 характеристичне рівняння;
характеристичне рівняння;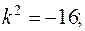
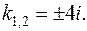
 де
де  довільні сталі.
довільні сталі.
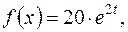 де
де 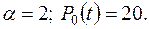
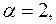 тобто число
тобто число 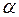 не є коренем характеристичного рівняння відповідного однорідного диф. рівняння, тоді, згідно (1.49), частинний розв'язок заданого диф. рівняння дорівнює:
не є коренем характеристичного рівняння відповідного однорідного диф. рівняння, тоді, згідно (1.49), частинний розв'язок заданого диф. рівняння дорівнює: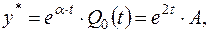 де
де  невідомий коефіцієнт, який необхідно знайти. Для цього диференціюємо вираз частинного розв'язку
невідомий коефіцієнт, який необхідно знайти. Для цього диференціюємо вираз частинного розв'язку 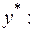
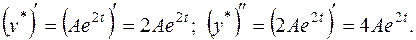
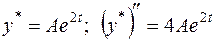 в отримане диф. рівняння:
в отримане диф. рівняння: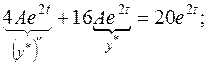


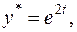 тоді
тоді 
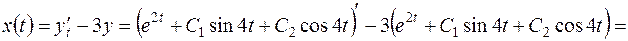
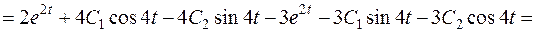
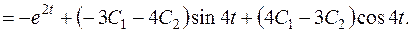



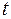 її перше рівняння
її перше рівняння  .
.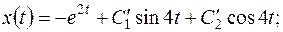

 довільні сталі.
довільні сталі.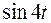 і
і 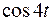 .
.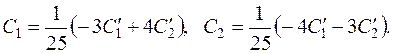
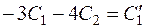 і
і  , справедливість яких доводить тотожність відповідей.
, справедливість яких доводить тотожність відповідей.


