
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Національний університет біоресурсів і природокористування УкраїниСодержание книги
Поиск на нашем сайте
Національний університет біоресурсів і природокористування України Ніжинський агротехнічний інститут Кафедра природничо-фундаментальних дисциплін
Муквич М.М. ЗВИЧАЙНІ ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ Навчальний посібник з дисципліни "Вища математика" для самостійної роботи студентів Технічних напрямів підготовки
Ніжин –2013 УДК 517.9 (073)
Рекомендовано до друку Вченою Радою Ніжинського агротехнічного інституту Національного університету біоресурсів і природокористування України
Протокол №9 від 26.06.2013 р.
Рецензенти: В.М. Лось, к. ф.-м. наук, доцент, завідувач кафедри вищої та прикладної математики Чернігівського державного технологічного університету Н.В. Майбородіна, к. ф.-м. наук, старший викладач кафедри природничо-фундаментальних дисциплін Ніжинського агротехнічного інституту
Муквич М.М. Звичайні диференціальні рівняння: навчальний посібник з дисципліни "Вища математика" для самостійної роботи студентів технічних напрямів підготовки / Муквич М.М. – Ніжин: Видавець ПП Лисенко М.М, 2013. – 92 с.
У навчальному посібнику наведено короткі теоретичні відомості розділу «Диференціальні рівняння» з дисципліни "Вища математика", індивідуальні контрольні завдання та зразки їх розв’язань. До індивідуальних контрольних завдань подано відповіді. Для самостійної роботи студентів напрямів підготовки: 6.100101 «Енергетика та електротехнічні системи в агропромисловому комплексі» та 6.100102 «Процеси, машини та обладнання агропромислового виробництва».
© Муквич М.М., 2013 © ПП Лисенко М.М., 2013 ВСТУП
Звичайні диференціальні рівняння широко застосовуються у дисциплінах професійної підготовки майбутніх інженерів-електриків та інженерів-механіків агропромислового виробництва. Тому метою даного навчального посібника є створення сприятливих умов для самостійного формування в студентів навичок до використання відповідних математичних методів у технічних розрахунках та дослідженнях. У навчальному виданні розглянуто контрольні завдання згідно тем індивідуальних (розрахунково-графічних) завдань, наведених у програмах з навчальної дисципліни «Вища математика», для підготовки фахівців ОКР «бакалавр» напрямів підготовки: 6.100101 «Енергетика та електротехнічні системи в агропромисловому комплексі» у вищих навчальних закладах II – IV рівнів акредитації Міністерства аграрної політики України (автори Ю.Б. Гнучій, Н.Г. Батечко, О.Ю. Дюженкова, Р.Ф. Овчар, О.І. Завгородній. – Київ: Аграрна освіта, 2010); 6.100102 «Процеси, машини та обладнання агропромислового виробництва» у вищих навчальних закладах II – IV рівнів акредитації Міністерства аграрної політики України (автори Ю.Б. Гнучій, Н.Г. Батеч-ко, О.Ю. Дюженкова, Р.Ф. Овчар, О.І. Завгородній, В.І. Кравець. – Київ: Аграрна освіта, 2010).
Найбільш важливі терміни та умови прикладів посібника виділено курсивом. Терміни, які означуються при вивченні даних розділів дисципліни, виділено напівжирним курсивом. Початок і кінець наведеного розв’язку завдання в навчальному посібнику позначено символами
Диференціальні рівняння першого порядку та деякі види Диференціальних рівнянь вищих порядків. Диференціальні рівняння першого порядку З відокремлюваними змінними
Щоб розв'язати це диф. рівняння відокремимо його змінні, записавши його у вигляді рівності диференціалів. Для цього замінимо в рівнянні
Домножимо обидві частини диф. рівняння на
Вважаючи, що у даному рівнянні
Рівняння (1.5 Із останньої рівності отримаємо загальний інтеграл диференціаль-ного рівняння (1.5):
де
Щоб класифікувати дане диф. рівняння запишемо його у нормальній формі (1.2): Відокремимо змінні та зведемо дане рівняння до вигляду (1.5 Замінимо в рівнянні
Домножимо обидві частини диф. рівняння на
Вважаючи, що у даному рівнянні
Розв'яжемо задачу Коші, використавши початкову умову: Знайдемо Відповідь. При відокремленні змінних диф. рівняння (1.5) отримали його у диференціальній формі (стр. 9):
Отримали диф. рівняння (1.6) з відокремлюваними змінними.
Поділимо обидві частини рівняння на вираз
Використаємо формули №4 та №1 таблиці (3) невизначених інтегралів.
Використаємо початкову умову звідки Відповідь.
Маємо диференціальне рівняння виду (1.7). Уведемо заміну: Диференціюємо заміну по змінній Підставивши в останню рівність вираз Звідси Використавши формулу №15 таблиці (3) невизначених інтегралів, отримаємо:
Відповідь. Інтегрується в квадратурах. Загальний розв'язок рівняння (1.27) знаходять за допомогою
|
 Розв'язати диференціальне рівняння:
Розв'язати диференціальне рівняння:

 Розв'язання.
Розв'язання.

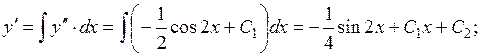

загальний розв’язок рівняння.
Значення довільних сталих  знайдемо, використовуючи задані початкові умови
знайдемо, використовуючи задані початкові умови 
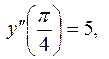 тоді, підставивши у першу рівність
тоді, підставивши у першу рівність  значення
значення  отримаємо:
отримаємо: 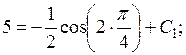
 звідки
звідки 
Врахувавши, що  отримаємо:
отримаємо: 
 тоді маємо рівняння:
тоді маємо рівняння:  звідки
звідки 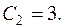
Врахувавши, що  отримаємо:
отримаємо: 
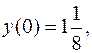 тоді, підставивши в останню рівність
тоді, підставивши в останню рівність  отримаємо:
отримаємо:
 звідки
звідки 
Відповідь.  частинний розв'язок.
частинний розв'язок. 
 Диференціальне рівняння виду Диференціальне рівняння виду 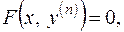 яке можна розв'язати відносно яке можна розв'язати відносно  : :
Інтегрується в квадратурах. Використовуючи заміну звідки
При цьому загальний розв'язок диф. рівняння (1.28) отримують у параметричній формі: |
 Розв'язати диференціальне рівняння:
Розв'язати диференціальне рівняння: 
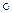 Розв'язання.
Розв'язання.
Записавши дане рівняння у вигляді  , отримаємо рівняння (1.28).
, отримаємо рівняння (1.28).
Нехай  , тоді останню рівність запишемо у вигляді:
, тоді останню рівність запишемо у вигляді:
 звідки
звідки 
Задано рівняння другого порядку, тобто  тоді, використовуючи залежність (1.28*), отримаємо:
тоді, використовуючи залежність (1.28*), отримаємо:


 Відповідь.
Відповідь. 

Основні означення
 Диференціальне рівняння виду:
Диференціальне рівняння виду:

| (1.31) |
де  задані функції, називається лінійним диференціальним рівнянням
задані функції, називається лінійним диференціальним рівнянням  го порядку.
го порядку.
 Функції
Функції  називаються коефіцієнтами даного рівняння, функція
називаються коефіцієнтами даного рівняння, функція  вільний член диф. рівняння (1.31). Вважатимемо вказані функції – неперервними на деякому інтервалі
вільний член диф. рівняння (1.31). Вважатимемо вказані функції – неперервними на деякому інтервалі 
 Якщо
Якщо  , то рівняння (1.31) називають лінійним неоднорідним диференціальним рівнянням
, то рівняння (1.31) називають лінійним неоднорідним диференціальним рівнянням  го порядку.
го порядку.
Якщо  , то диф. рівняння (1.31) називають лінійним однорідним диференціальним рівнянням
, то диф. рівняння (1.31) називають лінійним однорідним диференціальним рівнянням  го порядку.
го порядку.

 , бо інакше рівняння (1.31) не є диф. рівнянням
, бо інакше рівняння (1.31) не є диф. рівнянням  го порядку. Поділимо обидві частини рівняння (1.31) на
го порядку. Поділимо обидві частини рівняння (1.31) на  , тоді отримаємо лінійне диф. рівняння виду:
, тоді отримаємо лінійне диф. рівняння виду:
де Лінійне диференціальне рівняння
|
Список рекомендованої літератури
1. Дубовик В.П. Вища математика: навч. посiбник / В.П. Дубовик, І.І. Юрик. – К.: Вища шк., 2004. – С. 421– 493.
2. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. – М.: Наука, 1982. – 576 с.
3. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. – М.: Наука, 1982. – 332 с.
4. Самойленко А.М. Диференціальні рівняння / А.М. Самойленко, М.О. Перестюк, І.О. Парасюк. – К.: Либідь, 1994. – 360 с.
5. Шестаков А.А. Курс высшей математики: Учеб. для студентов втузов / А.А. Шестаков, И.А. Малышева, Д.П. Полозков; под ред. А.А. Шеста-кова. – М.: Высш. шк., 1987. – С.125–230.
6. Шкіль М.І. Вища математика / М.І. Шкіль, Т.В. Колесник. – К: Вища шк., 1986. – С.183–299.
7. Шкіль М.І. Звичайні диференціальні рівняня / М.І. Шкіль, М.А. Сотни-ченко. – К: Вища шк., 1992. – 303 с.
8. Вища математика. Збірник задач: навч. посібник / [Дубовик В.П., Юрик І.І., Вовкодав І.П. та ін.]; за ред. В.П. Дубовика, І.І. Юрика. – К.: АСК, 2001. – 480с.
9. Гудименко Ф.С. Збірник задач з вищої математики: Учб. посібник для студентів природничих факультетів університетів / Ф.С. Гудименко, Д.М. Борисенко, В.О. Волкова та ін.; за ред. Ф.С. Гудименка. – К.: Вид-во Київського університету, 1967. – 352 с.
ІМЕННИЙ ПОКАЖЧИК
Абель Нільс Хенрік (1802–1829) – норвезький математик
Бернуллі Йоган (1667–1748) – швейцарський математик
Бернуллі Якоб (1654–1705) – швейцарський математик, родоначальник династії
видатних учених математиків і механіків
Вронський Юзеф (1776–1853) – польський математик
Ейлер Леонард (1707–1783) – швейцарський математик, механік, фізик
Коші Огюстен Луї (1789–1857) – французський математик
Крамер Габриель (1704–1752) – швейцарський математик
Лагранж Жозеф (1736–1813) – французський математик
Ріккаті Джакопо Франческо (1676–1754) – італійський математик
ПРЕДМЕТНИЙ ПОКАЖЧИК
В изначник Вронського (вронскіан) – стр. 45;
Д иференціальне рівняння – стр. 4;
– Бернуллі – стр. 28;
– в частинних похідних – стр. 4;
– допускає пониження порядку – стр. 40; 41;
– звичайне – стр. 4;
– з відокремлюваними змінними – стр. 9; 11.
– інтегрується в квадратурах – cтр. 8;
– лінійне (першого порядку)– стр. 22;
– лінійне ( порядку)– стр. 43; 66;
порядку)– стр. 43; 66;
– лінійне неоднорідне другого порядку із сталими
коефіцієнтами – стр. 53;
– лінійне однорідне другого порядку із сталими
коефіцієнтами – стр. 50;
– неявне (першого порядку)– стр. 5;
– неявне ( го порядку)– стр. 35;
го порядку)– стр. 35;
– нерозв'язне відносно похідної (першого порядку) –
стр. 5;
– нормальне або явне ( го порядку)– стр. 35;
го порядку)– стр. 35;
– однорідне (першого порядку) – стр. 13;
– першого порядку – стр. 5;
– Ріккаті – стр. 28;
– у повних диференціалах – стр. 39;
– у нормальній формі (першого порядку)– стр. 5;
–  го порядку – стр. 35;
го порядку – стр. 35;
З агальний інтеграл диф. рівняння першого порядку – стр. 8;
загальний розв'язок диф. рівняння першого порядку – стр. 8;
задача Коші – стр.7;36;
І зокліна – стр.8;
інтегральна крива диференціального рівняння – стр. 4; 35;
інтегрувальний множник – стр. 31;
Л інійно залежні функції – стр.44;
лінійно незалежні функції – стр.45;
лінійне неоднорідне диф. рівняння  го порядку – стр. 43; 66;
го порядку – стр. 43; 66;
– другого порядку – стр. 47;
– другого порядку із сталими
коефіцієнтами – стр. 53;
лінійне однорідне диф. рівняння  го порядку – стр. 43; 66;
го порядку – стр. 43; 66;
– другого порядку – стр. 44;
– другого порядку із сталими
коефіцієнтами – стр. 50;
М етод Бернуллі інтегрування лінійного диф. рівняння  го порядку –
го порядку – 
стр. 23;
– варіації довільних сталих (Лагранжа) – стр. 47;
– виключення змінної – стр. 69;
Н ормальна система диференціальних рівнянь – стр. 68;
О днорідна функція  го виміру – стр. 13;
го виміру – стр. 13;
– нульового виміру – стр. 13;
особлива інтегральна крива – стр.7;
– точка – стр.7;
особливий розв'язок диференціального рівняння – стр.7;
П оле напрямів – стр.8;
порядок диференціального рівняння – стр. 4;
початкова умова розв'язку – стр. 7; 36;
Р озв'язок диференціального рівняння – стр. 4; 35;
– загальний – стр.8; 36;
– частинний – стр.8;36;
С пеціальна права частина лінійного неоднорідного диф. рівняння
другого порядку із сталими коефіцієнтам – стр. 53;
Т еорема Коші (про існування і єдиність розв'язку диференціального
рівняння першого порядку) – стр.6;
– Коші (про існування і єдиність розв'язку диференціального
рівняння  го порядку) – стр.36;
го порядку) – стр.36;
– про накладання розв'язків – стр. 47;
– про структуру загального розв’язку лінійного однорідного диф.
рівняння другого порядку – стр. 45;
– про структуру загального розв’язку лінійного неоднорідного диф.
рівняння другого порядку – стр. 49;
Ф ормула Абеля – стр. 46; 66;
Х арактеристичне рівняння – стр. 50;
Ч астинний інтеграл диф. рівняння першого порядку – стр. 8;
частинний розв'язок диф. рівняння першого порядку – стр. 8;
ДОДАТКИ
Таблиця 1.
Диференціювання функцій
Правила диференціювання.
Якщо функції  диференційовні в точці диференційовні в точці  , тоді виконуються рівності: , тоді виконуються рівності:
  де де 
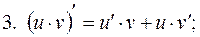  5. Похідна складеної функції:
5. Похідна складеної функції:

| |
Диференціал функції  знаходять за формулою: знаходять за формулою:

| |
| Таблиця похідних | |
 де де 
| 
|
 де де 
| 
|
 де де 
| 
|
 де де
| 
|

| Похідні гіперболічних функцій
   
|

| |

| 
|

| 
|

| 
|

| 
|
Таблиця 2.
Таблиця 3.
Таблиця невизначених інтегралів
( довільна стала інтегрування)
довільна стала інтегрування)

| 
|

| |

| 
|

| 
|

| 
|

| 
|

| 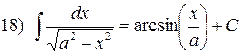
|

| Інтеграли від гіперболічних функцій |

| 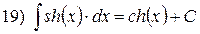
|
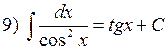
| 
|

| 
|

| 
|
ЗМІСТ
Вступ.............................................................................................................. 3
Звичайні диференціальні рівняння (Короткі теоретичні відомості)........ 4
Національний університет біоресурсів і природокористування України
|
| Поделиться: |

 та
та  відповідно.
відповідно.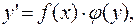
 і
і  задані і неперервні на деякому інтервалі функції, нази-вається диференціальним рівнянням з відокремлюваними змінними.
задані і неперервні на деякому інтервалі функції, нази-вається диференціальним рівнянням з відокремлюваними змінними. на
на  тоді отримаємо:
тоді отримаємо:


 поділимо обидві його частини на
поділимо обидві його частини на 

 )
)

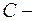 довільна стала.
довільна стала.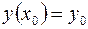 , то необхідно знайти конкретне значення
, то необхідно знайти конкретне значення  підставивши в загальний інтеграл
підставивши в загальний інтеграл  і
і  замість
замість  (тобто розв'язати задачу Коші).
(тобто розв'язати задачу Коші).
 ;
; 
 ;
; 
 диф. рівняння з відокремлю-ваними змінними (1.5), бо
диф. рівняння з відокремлю-ваними змінними (1.5), бо 


 поділимо обидві його частини на
поділимо обидві його частини на 

 де
де  довільна стала.
довільна стала.

 звідки
звідки 
 загальний розв'язок диф. рівняння.
загальний розв'язок диф. рівняння.
 звідки
звідки 
 частинний розв'язок диф. рівняння
частинний розв'язок диф. рівняння 

 ,
, 

 звідки
звідки  .
. Після скорочення отримаємо диференціальне рівняння, змінні якого – відокремлені:
Після скорочення отримаємо диференціальне рівняння, змінні якого – відокремлені:
 де
де 


 звідки
звідки 
 загальний інтеграл.
загальний інтеграл.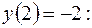


 частинний інтеграл.
частинний інтеграл. 
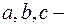 задані числа, зводиться до рівняння з відокремленими змінними (1.5) за допомогою заміни:
задані числа, зводиться до рівняння з відокремленими змінними (1.5) за допомогою заміни: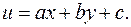
 звідки отримаємо диф. рівняння
звідки отримаємо диф. рівняння  з відок-ремлюваними змінними.
з відок-ремлюваними змінними.
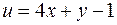 , тоді задане рівняння має вигляд
, тоді задане рівняння має вигляд 

 або
або 
 отримаємо:
отримаємо: 





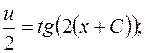

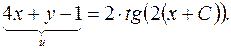

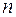 інтегрувань:
інтегрувань:
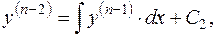 .........
.........


 отримаємо рівняння
отримаємо рівняння 
 . Після цього рівняння (1.28) розв'язують аналогічно до диференціального рівняння (1.27), інтегруючи
. Після цього рівняння (1.28) розв'язують аналогічно до диференціального рівняння (1.27), інтегруючи 








