Лінійні неоднорідні диф. рівняння другого порядку із сталими коефіцієнтами. Рівняння зі спеціальною правою частиною
Похожие статьи вашей тематики
Розглянемо лінійне неоднорідне диф. рівняння другого порядку із сталими коефіцієнтами:

| (1.46)
| де  і і  сталі числа, сталі числа,  задана неперервна на проміжку задана неперервна на проміжку  функція. функція.

За теоремою (1.38) загальний розв’язок  даного рівняння дорівнює: даного рівняння дорівнює:
 , ,
де  частинний розв’язок рівняння (1.46), частинний розв’язок рівняння (1.46),  загальний розв’язок відповідного однорідного рівняння. загальний розв’язок відповідного однорідного рівняння.
Знаходження загального розв'язку 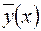 відповідного однорідного рівняння (1.41) за формулами (1.43–1.45), зазвичай, не викликає труднощів. Частинний розв'язок відповідного однорідного рівняння (1.41) за формулами (1.43–1.45), зазвичай, не викликає труднощів. Частинний розв'язок  завжди можна знайти методом варіації довільних сталих (1.39–1.40). Але для рівнянь із спеціальною правою частиною завжди можна знайти методом варіації довільних сталих (1.39–1.40). Але для рівнянь із спеціальною правою частиною  частинний розв'язок частинний розв'язок  можна знайти простіше, не використовуючи операцію інтегрування. можна знайти простіше, не використовуючи операцію інтегрування.

Нехай права частина диф. рівняння (1.46) має вигляд:
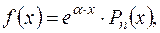
| (1.47)
| де  дійсне число, дійсне число,  многочлен степеня многочлен степеня 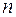 . .
Тоді частинний розв'язок  заданого рівняння шукають у вигляді: заданого рівняння шукають у вигляді:

| (1.48)
| де 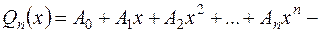 многочлен з невизначеними коефіцієнтами того ж самого степеня, що й многочлен многочлен з невизначеними коефіцієнтами того ж самого степеня, що й многочлен 
 число коренів характеристичного рівняння відповідного однорід-ного диф. рівняння (1.41), які дорівнюють число коренів характеристичного рівняння відповідного однорід-ного диф. рівняння (1.41), які дорівнюють 
Якщо 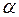 не є коренем характеристичного рівняння, то приймають не є коренем характеристичного рівняння, то приймають 
|  Для заданого диф. рівняння (1.46) пошук частинного розв'язку
Для заданого диф. рівняння (1.46) пошук частинного розв'язку  у вигляді(1.48)має три випадки.
1. Число у вигляді(1.48)має три випадки.
1. Число 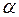 у спеціальній правій частині рівняння (1.47) у спеціальній правій частині рівняння (1.47)  не є коренемхарактеристичного рівняння відповідного однорідного диф. рівняння (1.41), тобто не є коренемхарактеристичного рівняння відповідного однорідного диф. рівняння (1.41), тобто  і і ,томуу формулі (1.48): ,томуу формулі (1.48):  .
Тоді частинний розв'язок .
Тоді частинний розв'язок  заданого рівняння (1.46) шукають у вигляді: заданого рівняння (1.46) шукають у вигляді:

| (1.49)
| де 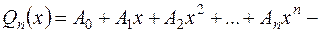 многочлен з невизначеними коефі-цієнтами того ж самого степеня, що й многочлен многочлен з невизначеними коефі-цієнтами того ж самого степеня, що й многочлен 
2. Число 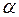 є простим коренем характеристичного рівняння відповідного однорідного диф. рівняння (1.41), тобто є простим коренем характеристичного рівняння відповідного однорідного диф. рівняння (1.41), тобто  або або  , при , при  , томуу формулі (1.48): , томуу формулі (1.48):  . .
Тоді частинний розв'язок  заданого рівняння (1.46) шукають у вигляді: заданого рівняння (1.46) шукають у вигляді:

| (1.50)
|
3. Число 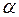 є двократним коренем характеристичного рівняння відповідного однорідного диф. рівняння (1.41), тобто є двократним коренем характеристичного рівняння відповідного однорідного диф. рівняння (1.41), тобто  , томуу формулі (1.48): , томуу формулі (1.48):  . .
Частинний розв'язок  заданого рівняння (1.46) має вигляд: заданого рівняння (1.46) має вигляд:

| (1.51)
|
 Якщо права частина (1.47) має вигляд Якщо права частина (1.47) має вигляд  тобто тобто  тоді у формулах (1.49–1.51): тоді у формулах (1.49–1.51):  невідоме число. невідоме число.
 Невідомі коефіцієнти Невідомі коефіцієнти  многочлена многочлена 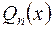 знаходять методом невизначених коефіцієнтів, підставивши знаходять методом невизначених коефіцієнтів, підставивши  у задане диф. рівняння (1.46). у задане диф. рівняння (1.46).
|  Розв'язати диференціальне рівняння: Розв'язати диференціальне рівняння: 
 Розв'язання. Розв'язання.
За теоремою (1.38) загальний розв'язок заданого рівняння дорівнює:
 , ,
де  частинний розв’язок заданого диф. рівняння, частинний розв’язок заданого диф. рівняння,
 загальний розв’язок відповідного однорідного рівняння. загальний розв’язок відповідного однорідного рівняння.
Розглянемо відповідне однорідне диф. рівняння:
  характеристичне рівняння; характеристичне рівняння;
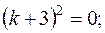 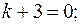  
За формулою (1.45) загальний розв'язок відповідного однорідного диф. рівняння дорівнює:
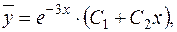 де де  довільні сталі. довільні сталі.
Спеціальна права частина заданого рівняння має вигляд (1.47):
 де де 
 тобто число тобто число 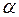 не є коренем характеристичного рівняння відповідного однорідного диф. рівняння, тоді, згідно (1.49), частинний розв'язок заданого диф. рівняння дорівнює: не є коренем характеристичного рівняння відповідного однорідного диф. рівняння, тоді, згідно (1.49), частинний розв'язок заданого диф. рівняння дорівнює:
 де де  невідомі коефіцієнти, які необхідно знайти. невідомі коефіцієнти, які необхідно знайти.
 Для позначення невідомих коефіцієнтів Для позначення невідомих коефіцієнтів  многочлена многочлена 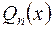 , при невисоких його степенях, зазвичай, використо-вують змінні , при невисоких його степенях, зазвичай, використо-вують змінні 
| Підставимо  у задане диф. рівняння: у задане диф. рівняння:
 
Прирівняємо коефіцієнти:   звідки звідки 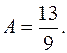
Тому  тоді тоді 
Відповідь.  де де  довільні сталі. довільні сталі. 
 Розв'язати диференціальне рівняння: Розв'язати диференціальне рівняння: 
 Розв'язання. Розв'язання.
За теоремою (1.38) загальний розв'язок заданого рівняння дорівнює:
 , ,
де  частинний розв’язок заданого диф. рівняння, частинний розв’язок заданого диф. рівняння,
 загальний розв’язок відповідного однорідного рівняння. загальний розв’язок відповідного однорідного рівняння.
Розглянемо відповідне однорідне диф. рівняння:
  характеристичне рівняння. характеристичне рівняння.
За теоремою Вієта: 
За формулою (1.43) загальний розв'язок відповідного однорідного диф. рівняння дорівнює:
 де де  довільні сталі. довільні сталі.
Спеціальна права частина заданого рівняння має вигляд (1.47):
 де де 
 тобто число тобто число 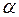 є простим коренем характеристичного рівняння відповідного однорідного диф. рівняння, тоді, згідно (1.50), частинний розв'язок заданого диф. рівняння дорівнює: є простим коренем характеристичного рівняння відповідного однорідного диф. рівняння, тоді, згідно (1.50), частинний розв'язок заданого диф. рівняння дорівнює:
 де де  невідомий коефіцієнт, який необхідно знайти. Диференціюємо вираз частинного розв'язку невідомий коефіцієнт, який необхідно знайти. Диференціюємо вираз частинного розв'язку 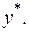



Частинний розв'язок  перетворює задане рівняння у правильну рівність відносно перетворює задане рівняння у правильну рівність відносно  Підставимо знайдені вирази Підставимо знайдені вирази  , ,   у задане рівняння замість у задане рівняння замість  відповідно: відповідно:

Поділивши обидві частини рівності на  отримаємо: отримаємо:

 звідси, звідси, 
тоді загальний розв'язок  заданого рівняння дорівнює: заданого рівняння дорівнює:
 де де  довільні сталі. довільні сталі.
  звідки звідки 
Диференціюємо вираз загального розв'язку заданого рівняння:


  звідки звідки 
 додавши почленно рівняння системи, отримаємо: додавши почленно рівняння системи, отримаємо:
 
Виразимо із першого рівняння системи: 
Підставивши значення 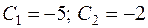 у загальний розв'язок у загальний розв'язок  , отримаємо частинний розв'язок заданого рівняння: , отримаємо частинний розв'язок заданого рівняння:

Відповідь.  
Зразки виконання контрольного завдання №4.
 Розв'язати диференціальне рівняння: Розв'язати диференціальне рівняння: 
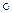 Розв'язання. Розв'язання.
За теоремою (1.38) загальний розв'язок заданого рівняння дорівнює:
 , ,
де  частинний розв’язок заданого диф. рівняння, частинний розв’язок заданого диф. рівняння,
 загальний розв’язок відповідного однорідного рівняння. загальний розв’язок відповідного однорідного рівняння.
Розглянемо відповідне однорідне диф. рівняння:
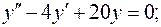  характеристичне рівняння; характеристичне рівняння;

 тобто тобто 
За формулою (1.44) загальний розв'язок заданого диф. рівняння дорівнює:
 де де  довільні сталі. довільні сталі.
Спеціальна права частина заданого рівняння має вигляд (1.47):
 де де 
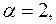  і і 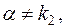 тобто число тобто число 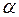 не є коренем характеристичного рівняння відповідного однорідного диф. рівняння, тоді, згідно (1.49), частинний розв'язок заданого диф. рівняння дорівнює: не є коренем характеристичного рівняння відповідного однорідного диф. рівняння, тоді, згідно (1.49), частинний розв'язок заданого диф. рівняння дорівнює:
 де де  невідомі коефіцієнти, які необхідно знайти. Для цього знайдемо: невідомі коефіцієнти, які необхідно знайти. Для цього знайдемо:





Частинний розв'язок  перетворює задане рівняння у правильну рівність відносно перетворює задане рівняння у правильну рівність відносно  Підставимо знайдені вирази Підставимо знайдені вирази  , ,   у задане рівняння замість у задане рівняння замість  відповідно: відповідно:
 Поділивши обидві частини рівності на Поділивши обидві частини рівності на  отримаємо: отримаємо:


Використовуючи метод невизначених коефіцієнтів, отримаємо:
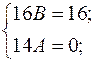 
Звідси,  тоді тоді
 де де  довільні сталі. довільні сталі.
Відповідь.  
 Розв'язати диференціальне рівняння: Розв'язати диференціальне рівняння: 
 Розв'язання. Розв'язання.
За теоремою (1.38) загальний розв'язок заданого рівняння дорівнює:
 , ,
де  частинний розв’язок заданого диф. рівняння, частинний розв’язок заданого диф. рівняння,
 загальний розв’язок відповідного однорідного рівняння. загальний розв’язок відповідного однорідного рівняння.
Розглянемо відповідне однорідне диф. рівняння:
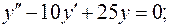  характеристичне рівняння; характеристичне рівняння;

За формулою (1.45) загальний розв'язок заданого диф. рівняння дорівнює:
 де де  довільні сталі. довільні сталі.
Спеціальна права частина заданого рівняння має вигляд (1.47):
 де де 
 , тобто число , тобто число 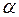 є двократним коренем характеристичного рівняння відповідного однорідного диф. рівняння, тоді, згідно (1.51), частинний розв'язок заданого диф. рівняння дорівнює: є двократним коренем характеристичного рівняння відповідного однорідного диф. рівняння, тоді, згідно (1.51), частинний розв'язок заданого диф. рівняння дорівнює:
 де де 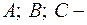 невідомі коефі-цієнти, які необхідно знайти. невідомі коефі-цієнти, які необхідно знайти.




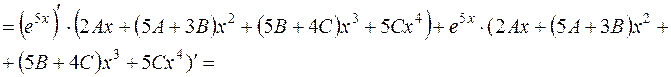




Підставимо знайдені вирази  , ,   у задане рівняння замість у задане рівняння замість  відповідно: відповідно:
 Поділивши обидві частини рівності на Поділивши обидві частини рівності на  отримаємо: отримаємо:


У лівій частині рівності згрупуємо вирази за степенями многочлена:


Прирівняємо коефіцієнти у лівій і правій частині рівності при однакових степенях (метод невизначених коефіцієнтів):
 
Звідси, 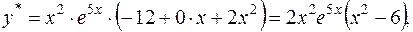 тоді тоді
 де де  довільні сталі. довільні сталі.
Відповідь.  
 Розв'язати диференціальне рівняння: Розв'язати диференціальне рівняння: 
 Розв'язання. Розв'язання.
Загальний розв'язок  заданого рівняння дорівнює: заданого рівняння дорівнює:  , ,
де  частинний розв’язок заданого диф. рівняння, частинний розв’язок заданого диф. рівняння,
 загальний розв’язок відповідного однорідного рівняння. загальний розв’язок відповідного однорідного рівняння.
 відповідне однорідне диф. рівняння; відповідне однорідне диф. рівняння;
 характеристичне рівняння. характеристичне рівняння.
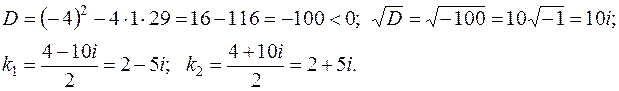
За формулою (1.44) загальний розв'язок відповідного однорідного диф. рівняння дорівнює:
 де де  довільні сталі. довільні сталі.
Спеціальна права частина заданого рівняння має вигляд (1.52):
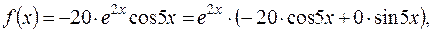 де де 

 тоді у виразі (1.53): тоді у виразі (1.53):  Тому частинний розв'язок заданого диф. рівняння, згідно (1.53), дорівнює: Тому частинний розв'язок заданого диф. рівняння, згідно (1.53), дорівнює:
 де де  і і  невідомі многочлени степеня невідомі многочлени степеня  , які необхідно знайти. Для цього диференціюємо вираз частинного розв'язку , які необхідно знайти. Для цього диференціюємо вираз частинного розв'язку  за правилом похідної добутку: за правилом похідної добутку:
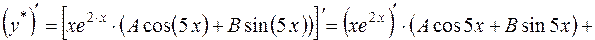

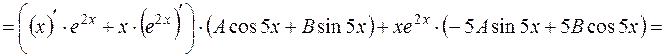


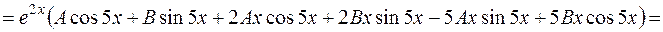


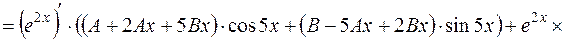







Підставимо знайдені вирази  , ,   у задане рівняння замість у задане рівняння замість  відповідно: відповідно:


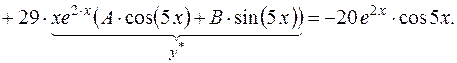
Поділимо обидві частини рівності на  розкриємо дужки і зведемо подібні доданки при розкриємо дужки і зведемо подібні доданки при  і і 
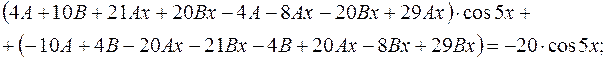
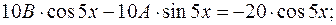
Прирівняємо коефіцієнти при  і і 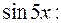 
тому 
Тоді частинний розв'язок дорівнює: 
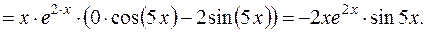
Запишемо загальний розв'язок  заданого рівняння: заданого рівняння:

де  довільні сталі. довільні сталі.
Відповідь.  
Зразок виконання контрольного завдання №4.
 Розв'язати диференціальне рівняння: Розв'язати диференціальне рівняння: 
 Розв'язання. Розв'язання.
За теоремою (1.38) загальний розв'язок заданого рівняння дорівнює:
 , ,
де  частинний розв’язок заданого диф. рівняння, частинний розв’язок заданого диф. рівняння,
 загальний розв’язок відповідного однорідного рівняння. загальний розв’язок відповідного однорідного рівняння.
Розглянемо відповідне однорідне диф. рівняння:   характеристичне рівняння. характеристичне рівняння.

За формулою (1.43) загальний розв'язок відповідного однорідного диф. рівняння дорівнює:
 де де  довільні сталі. довільні сталі.
Спеціальна права частина заданого рівняння має вигляд (1.54):
 де де 
 комплексне число, тому комплексне число, тому  і і  звідки звідки  Тоді, згідно (1.55) при Тоді, згідно (1.55) при  , частинний розв'язок заданого диф. рівняння дорівнює: , частинний розв'язок заданого диф. рівняння дорівнює:
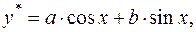 де де 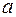 і і  невідомі коефіцієнти, які необхідно знайти. Для цього диференціюємо вираз частинного розв'язку невідомі коефіцієнти, які необхідно знайти. Для цього диференціюємо вираз частинного розв'язку 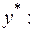


Підставимо знайдені вирази  , ,   у задане рівняння замість у задане рівняння замість  відповідно: відповідно:
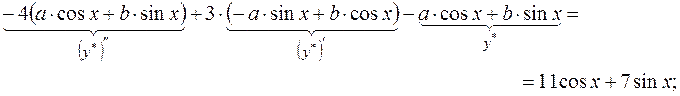


Прирівняємо коефіцієнти при 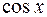 і і  
домножимо почленно перше рівняння системи на число 3, друге – на число (–5) і додамо рівняння:

 звідки звідки 
Підставимо  у перше рівняння системи: у перше рівняння системи:
  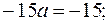 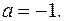
Звідси, частинний розв'язок  дорівнює: дорівнює: 
Запишемо загальний розв'язок  заданого рівняння: заданого рівняння:
 де де  довільні сталі. довільні сталі.
Відповідь.  
 Контрольні завдання №4 містять вправи на використання спеціальної правої частини виду: (1.49), (1.50), (1.51), (1.52), (1.54). Контрольні завдання №4 містять вправи на використання спеціальної правої частини виду: (1.49), (1.50), (1.51), (1.52), (1.54).
2.6. Лінійні диференціальні рівняння  го порядку із сталими коефіцієнтами го порядку із сталими коефіцієнтами
Розглянемо лінійне однорідне диференціальне рівняння  го порядку із сталими коефіцієнтами: го порядку із сталими коефіцієнтами:

| (1.55)
| де  сталі дійсні числа. сталі дійсні числа.
 Характеристичним для диф. рівняння (1.55) називається алгебраїчне рівняння Характеристичним для диф. рівняння (1.55) називається алгебраїчне рівняння  го порядку: го порядку:

| (1.56)
| яке, як відомо, має 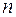 коренів: коренів: 

1) Кожному простому кореню  рівняння (1.56) відповідає частинний розв’язок рівняння (1.56) відповідає частинний розв’язок  диф. рівняння (1.55), а кожному кореню диф. рівняння (1.55), а кожному кореню  кратності кратності  відповідає відповідає  частинних розв’язків виду: частинних розв’язків виду:

2) Кожній порі  простих комплексно-спряжених коренів рівняння (1.55) відповідає два частинних розв’язки простих комплексно-спряжених коренів рівняння (1.55) відповідає два частинних розв’язки  і і 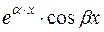 диф. рівняння (1.55), а кожній парі диф. рівняння (1.55), а кожній парі  комплексно- спряжених коренів кратності комплексно- спряжених коренів кратності  відповідає відповідає  частинних розв’язків виду: частинних розв’язків виду: 

3) Позначивши знайдені лінійно-незалежні частинні розв'язки через  , загальний розв'язок , загальний розв'язок  однорідного диф. рівняння (1.55) знаходиться за формулою: однорідного диф. рівняння (1.55) знаходиться за формулою:
 , ,
| (1.57)
| де  довільні сталі. довільні сталі.
 Диференціальне рівняння виду: Диференціальне рівняння виду:

| (1.58)
| є лінійним неоднорідним диференціальним рівнянням  го порядку із сталими коефіцієнтами. го порядку із сталими коефіцієнтами.
Загальний розв'язок диф. рівняння (1.58)  знаходять аналогічно до розв'язку лінійного неоднорідного диф. рівняння другого порядку з сталими коефіцієнтами. знаходять аналогічно до розв'язку лінійного неоднорідного диф. рівняння другого порядку з сталими коефіцієнтами.
 Розв'язати диференціальне рівняння: Розв'язати диференціальне рівняння: 
 Розв'язання. Розв'язання.
 характеристичне рівняння; характеристичне рівняння;
  або або 
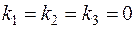 або або  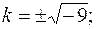 
За теоремою (стр. 66) знайденим кореням характеристичного рівняння відповідають частинні розв'язки:

Загальний розв'язок заданого рівняння знаходимо за формулою (1.57):

де 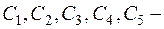 довільні сталі. довільні сталі.
Відповідь.  
|




 і
і  сталі числа,
сталі числа,  задана неперервна на проміжку
задана неперервна на проміжку  функція.
функція.
 даного рівняння дорівнює:
даного рівняння дорівнює: ,
, частинний розв’язок рівняння (1.46),
частинний розв’язок рівняння (1.46),  загальний розв’язок відповідного однорідного рівняння.
загальний розв’язок відповідного однорідного рівняння. відповідного однорідного рівняння (1.41) за формулами (1.43–1.45), зазвичай, не викликає труднощів. Частинний розв'язок
відповідного однорідного рівняння (1.41) за формулами (1.43–1.45), зазвичай, не викликає труднощів. Частинний розв'язок  завжди можна знайти методом варіації довільних сталих (1.39–1.40). Але для рівнянь із спеціальною правою частиною
завжди можна знайти методом варіації довільних сталих (1.39–1.40). Але для рівнянь із спеціальною правою частиною  частинний розв'язок
частинний розв'язок 
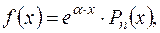
 дійсне число,
дійсне число,  многочлен степеня
многочлен степеня 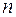 .
.
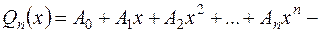 многочлен з невизначеними коефіцієнтами того ж самого степеня, що й многочлен
многочлен з невизначеними коефіцієнтами того ж самого степеня, що й многочлен 
 число коренів характеристичного рівняння відповідного однорід-ного диф. рівняння (1.41), які дорівнюють
число коренів характеристичного рівняння відповідного однорід-ного диф. рівняння (1.41), які дорівнюють 
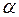 не є коренем характеристичного рівняння, то приймають
не є коренем характеристичного рівняння, то приймають 
 Для заданого диф. рівняння (1.46) пошук частинного розв'язку
Для заданого диф. рівняння (1.46) пошук частинного розв'язку  не є коренемхарактеристичного рівняння відповідного однорідного диф. рівняння (1.41), тобто
не є коренемхарактеристичного рівняння відповідного однорідного диф. рівняння (1.41), тобто  і
і ,томуу формулі (1.48):
,томуу формулі (1.48):  .
Тоді частинний розв'язок
.
Тоді частинний розв'язок 

 або
або  , при
, при  , томуу формулі (1.48):
, томуу формулі (1.48):  .
.
 , томуу формулі (1.48):
, томуу формулі (1.48):  .
.
 тобто
тобто  тоді у формулах (1.49–1.51):
тоді у формулах (1.49–1.51):  невідоме число.
невідоме число. многочлена
многочлена 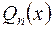 знаходять методом невизначених коефіцієнтів, підставивши
знаходять методом невизначених коефіцієнтів, підставивши  Розв'язати диференціальне рівняння:
Розв'язати диференціальне рівняння: 
 Розв'язання.
Розв'язання. частинний розв’язок заданого диф. рівняння,
частинний розв’язок заданого диф. рівняння, загальний розв’язок відповідного однорідного рівняння.
загальний розв’язок відповідного однорідного рівняння.
 характеристичне рівняння;
характеристичне рівняння;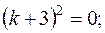
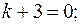


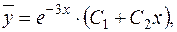 де
де  довільні сталі.
довільні сталі. де
де 
 тобто число
тобто число  де
де  невідомі коефіцієнти, які необхідно знайти.
невідомі коефіцієнти, які необхідно знайти.
 у задане диф. рівняння:
у задане диф. рівняння:


 звідки
звідки 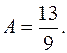
 тоді
тоді 
 де
де 


 характеристичне рівняння.
характеристичне рівняння.
 де
де  де
де 
 тобто число
тобто число  де
де  невідомий коефіцієнт, який необхідно знайти. Диференціюємо вираз частинного розв'язку
невідомий коефіцієнт, який необхідно знайти. Диференціюємо вираз частинного розв'язку 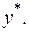



 перетворює задане рівняння у правильну рівність відносно
перетворює задане рівняння у правильну рівність відносно  Підставимо знайдені вирази
Підставимо знайдені вирази 
 у задане рівняння замість
у задане рівняння замість  відповідно:
відповідно:
 отримаємо:
отримаємо:
 звідси,
звідси, 
 де
де 
 звідки
звідки 



 звідки
звідки 
 додавши почленно рівняння системи, отримаємо:
додавши почленно рівняння системи, отримаємо:


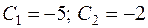 у загальний розв'язок
у загальний розв'язок 

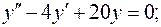
 характеристичне рівняння;
характеристичне рівняння;
 тобто
тобто 
 де
де  де
де 
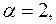
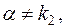 тобто число
тобто число  де
де 




 Поділивши обидві частини рівності на
Поділивши обидві частини рівності на  отримаємо:
отримаємо:

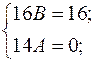

 тоді
тоді де
де 

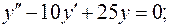
 характеристичне рівняння;
характеристичне рівняння;
 де
де  де
де 
 , тобто число
, тобто число  де
де 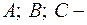 невідомі коефі-цієнти, які необхідно знайти.
невідомі коефі-цієнти, які необхідно знайти.



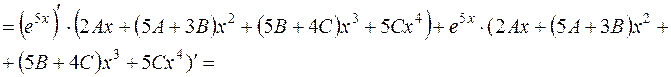




 Поділивши обидві частини рівності на
Поділивши обидві частини рівності на 





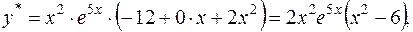 тоді
тоді де
де 
 Нехай права частина диф. рівняння (1.46)
Нехай права частина диф. рівняння (1.46) 
 дійсні числа,
дійсні числа,  многочлен степеня
многочлен степеня  .
.
 і
і  многочлени степеня
многочлени степеня  з невизначеними коефіцієнтами;
з невизначеними коефіцієнтами;  найвищий степінь многочленів
найвищий степінь многочленів  та
та  ;
;
 Функція (1.47) є окремим випадком спеціальної правої частини (1.52) і утворюється з неї при
Функція (1.47) є окремим випадком спеціальної правої частини (1.52) і утворюється з неї при 
 Якщо права частина диф. рівняння (1.46) є сумою декількох різних за будовою функцій виду (1.47) або (1.52), то для знаходження частинного розв'язку
Якщо права частина диф. рівняння (1.46) є сумою декількох різних за будовою функцій виду (1.47) або (1.52), то для знаходження частинного розв'язку  Зокрема, якщо права частина диф. рівняння (1.46)
Зокрема, якщо права частина диф. рівняння (1.46) 
 і
і  відомі дійсні числа,
відомі дійсні числа,
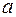 і
і  невідомі коефіцієнти;
невідомі коефіцієнти; .
.
 заданого рівняння дорівнює:
заданого рівняння дорівнює:  відповідне однорідне диф. рівняння;
відповідне однорідне диф. рівняння; характеристичне рівняння.
характеристичне рівняння.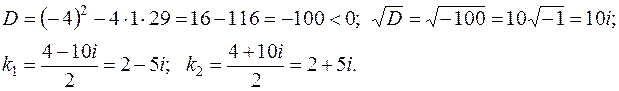
 де
де 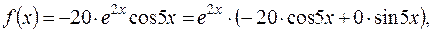 де
де 

 тоді у виразі (1.53):
тоді у виразі (1.53):  Тому частинний розв'язок заданого диф. рівняння, згідно (1.53), дорівнює:
Тому частинний розв'язок заданого диф. рівняння, згідно (1.53), дорівнює: де
де  і
і  невідомі многочлени степеня
невідомі многочлени степеня  , які необхідно знайти. Для цього диференціюємо вираз частинного розв'язку
, які необхідно знайти. Для цього диференціюємо вираз частинного розв'язку 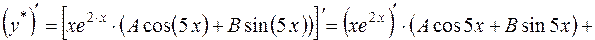

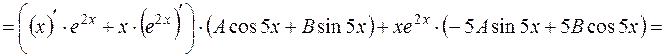


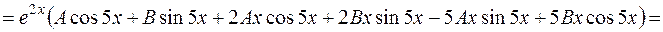


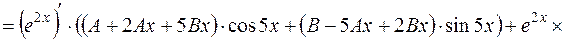








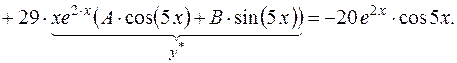
 і
і 
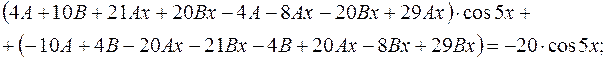
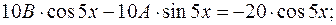
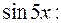



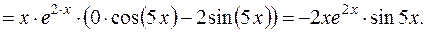




 характеристичне рівняння.
характеристичне рівняння.
 де
де  де
де 
 комплексне число, тому
комплексне число, тому  і
і  звідки
звідки 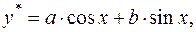 де
де 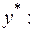


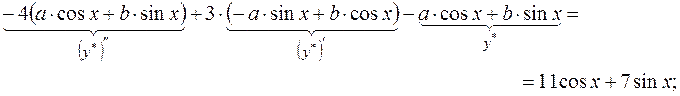


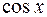 і
і 


 звідки
звідки 
 у перше рівняння системи:
у перше рівняння системи:
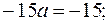
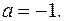

 де
де 
 го порядку із сталими коефіцієнтами
го порядку із сталими коефіцієнтами
 сталі дійсні числа.
сталі дійсні числа. Характеристичним для диф. рівняння (1.55) називається алгебраїчне рівняння
Характеристичним для диф. рівняння (1.55) називається алгебраїчне рівняння 


 рівняння (1.56) відповідає частинний розв’язок
рівняння (1.56) відповідає частинний розв’язок  диф. рівняння (1.55), а кожному кореню
диф. рівняння (1.55), а кожному кореню  відповідає
відповідає 
 простих комплексно-спряжених коренів рівняння (1.55) відповідає два частинних розв’язки
простих комплексно-спряжених коренів рівняння (1.55) відповідає два частинних розв’язки  і
і 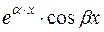 диф. рівняння (1.55), а кожній парі
диф. рівняння (1.55), а кожній парі  відповідає
відповідає  частинних розв’язків виду:
частинних розв’язків виду: 

 , загальний розв'язок
, загальний розв'язок  ,
,
 довільні сталі.
довільні сталі.

 характеристичне рівняння;
характеристичне рівняння;
 або
або 
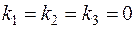 або
або 
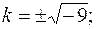



 довільні сталі.
довільні сталі.



