
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівняння математичної фізикиСодержание книги
Поиск на нашем сайте
Математичний аналіз 1. Межа функції (визначення по Коші і по Гейне). Визначення безперервності функції в точці. Теореми Вейєрштрасса і Больцано - Коші про функції, безперервних на відрізку. Рівномірна неперервність, теорема Кантора. 2. Дифференційованіть і похідна дійсної функції дійсного змінного. Геометричний зміст похідної. Основні теореми про диференційовні функції (теореми Ферма, Ролля, Лагранжа). Формула Тейлора із залишком у формі Пеано, у формі Лагранжа. 3. Визначення інтеграла Рімана. Інтегровність монотонних і безперервних функцій. Існування первісної у безперервної функції. Формула Ньютона - Лейбніца. 4. Числові ряди. Основні ознаки збіжності (ознака порівняння, Даламбера. Коші, інтегральна ознака) для рядів з невід'ємними членами. Ознака Лейбніца. Поняття абсолютної та умовної збіжності. Диференціальні рівняння 5. Задача Коші для диференціального рівняння першого порядку. Теорема існування та єдиності розв'язку задачі Коші. 6. Лінійні однорідні звичайні диференціальні рівняння n-го порядку з постійними коефіцієнтами. Метод Ейлера. 7. Лінійні неоднорідні звичайні диференціальні рівняння n-го порядку з постійними коефіцієнтами. метод Лагранжа Рівняння математичної фізики 8. Формулювання крайової задачі Штурма-Ліувілля. Звести задачу Штурма-Ліувілля до інтегрального рівняння. 9. Властивості власних значень і власних функцій задачі Штурма-Ліувілля. Довести теорему розкладання Стеклова. 10. Функція Гріна одновимірної крайової задачі. (В чому відмінність від фундаментальної функції). Довести теорему єдиності для функції Гріна 11. Дати визначення самосопряженної крайової задачі. Довести симетричність функції Гріна для самосопряженної крайової задачі. 12. Дати визначення фундаментальної та базисної систем рішень для одновимірної крайової задачі. Довести теорему існування для функції Гріна. Теорія ймовірностей 13. Дискретне простір елементарних подій. Операції над подіями. Класичне визначення ймовірності. Властивості ймовірності. 14. Умовні ймовірності. Незалежні події та їх властивості. 15. Випадкові величини. Функція розподілу випадкової величини та її властивості. 16. Числові характеристики випадкових величин: математичне сподівання, дисперсія та їх властивості. 17. Ланцюги Маркова. Матриці переходу за один і к-кроків для однорідного ланцюга Маркова. Функціональний аналіз 18. Лінійні оператори в лінійних нормованих просторах. Лінійне простір лінійних операторів (обмежених) 19. Абстрактні ряди Фурьє в Н. Теорема Рисса – Фішера. Теорема Гіильберта – Шмидта Аналіз данних 20. Інформаційні та аналітичні моделі. Учасники процесу аналізу даних. Формалізація даних. Основні етапи KDD. Класи задач, що вирішуються методами Data Mining 21. Алгоритми Data Mining - асоціативні правила. Характеристики значущості асоціативного правила 22. Аналіз рядів динамік. моделі прогнозування. Випадкові процеси 23. Випадкові процеси марківського типу. Рівняння Колмогорова. 24. Процеси не залежать від майбутнього. Теорема Колмогорова-Прохорова. Тотожність Вальда. 25. Коваріація та кореляція випадкового процесу. Взаємна коваріаційна і кореляційна функції випадкових процесів Похідна та інтеграл від випадкового процесу Теорія функцій комплексної змінної 26. Інтегральна теорема Коши. Інтегральна формула Коши. 27. Визначення лишку (вычета). Теорема про лишки. 28. Обчислення лишку у разі полюса. Обчислювальні методи 29. Теорема про LU-розкладання матриці. Метод Гауса. 30. PLU-розкладання невиродженої матриці. Метод Гауса з частковим (повним) вибором головного елемента. 31. Метод простої ітерації розв’язування СЛАР, необхідна й достатня умова збіжності. 32. Метод Ньютона розв’язку нелінійних рівнянь. 33. Інтерполяційний багаточлен Лагранжа. Залишковий член інтерполяційного багаточлена. 34. Інтерполяційний багаточлен Ньютона з розділеними різницями. Залишковий член інтерполяційного багаточлена. 35. Квадратурні формули Ньютона-Котеса (прямокутників, трапеції, Сімпсона). Моделювання екологічних, економічних та соціальних процесів 36. Загальне уявлення про системний аналіз, як про методологічну основу вивчення систем. 37. Класифікація, типи і приклади моделей 38. Поняття стійкості в математиці та в екології. Теорія керування 44. Найпростіша задача термінального керування. Принцип максимуму Понтрягіна. 45. Найпростіша задача термінального керування. Диференцiальний принцип максимуму. Наслiдок. 46. Оптимальне керування в лінійних системах. Керованість. Необхідна і достатня умова керованості. Методи оптимізації 47. Задачі лінійного програмування: їх типи; поняття плану; графічний метод розв'язування ЗЛП.. 48. Симплекс-метод для ЗЛП у стандартній формі. 49. М-метод для ЗЛП в загальному вигляді. 50. Методи побудови початкового плану і метод його поліпшення: метод північно-західного кута; метод мінімального елемента; метод потенціалів. 51. Ускладнені постановки ТЗ: обов'язкові і заборонені перевезення, обмеження на пропускну спроможність, задачі зі складами, ТЗ в мережевій постановці. 52. Основна теорема опуклого програмування Куна-Такера (з доведенням необхідності). Теорія множин 56. Поняття множини. Способи завдання множин. Визначення підмножини. Рівність двох множин. Операції над множинами: об'єднання, перетин, різниця, доповнення. Декартів добуток множин. 57. Висловлювання. Прості і складені висловлювання. Логічні зв'язки. Таблиці Куайна для логічних зв'язок. Характеристичні властивості логічних зв'язок. 58. Алфавіт алгебри висловлювань. Індуктивне визначення формули алгебри висловлень (ФАВ). Інтерпретація ФАВ. Таблиці Куайна для ФАВ. Класифікація ФАВ: здійсненні, опровержімие, тотожно істинні, тотожно хибні формули. Дискретна математика 59. Визначення графа. Способи завдання графів. Ізоморфізм графів. Маршрут, ланцюг, проста ланцюг. Цикл. Простий цикл. 60. Цикломатичне число графа. Теорема про Цикломатичне числі. Визначення дерева. Визначення лісу. Теорема про ліси. 61. Визначення булевой функції (БФ). Табличне завдання БФ. Елементарні БФ. 62. Основні класи БФ. Двоїсті функції. Самодвойственной функції. Монотонні функції. Істотні і фіктивні змінні. лінійні функції. Алгебра 63. Кільце многочленів над полем. Неприводимість над полем. Властивості неприводимих многочленів. Основна теорема про неприводими многочлени. Канонічне розкладання многочлена над полем. 64. Корені многочлена. Теорема Безу. Кратні корені многочлена. Критерій кратності кореня. 65. Основна теорема алгебри (б / д). Слідства з основної теореми для многочленів над полем Сі над полем R. 66. Повна лінійна група. Оборотність матриць. Критерій оборотності. 67. Скінченномірність. Базис і розмірність лінійного простору, властивості. Координати вектора в заданому базисі. Перехід до нового базису.. 68. Структура загального рішення однорідної СЛАР. Фундаментальна система рішень. Структура загального рішення неоднорідної СЛАР 69. Рівняння прямої і площини. Похідні види рівнянь. Взаємне розташування прямої і площини 70. Системи порівнянь першого ступеня. Китайська теорема про залишки. Порівняння по простому модулю. 71. Квадратичні лишки. Символ Лежандра та його властивості. Квадратичний закон взаємності. Символ Якобі. 72. Первісні корені по заданому модулю. Теорема існування первісної кореня по простому модулю. Програмування 86. Класифікація підпрограм. Поняття параметрів, їх класифікація. Формальні та фактичні параметри, способи передачі параметрів. 87. Керуючі структури. Класифікація базових структур. Властивості базових структур. Поняття оператора в мові С + +. Реалізація керуючих структур. 88. Конструюються типи даних. Масиви. Записи. Особливості реалізації в мовах програмування. 89. Робота з покажчиками. Динамічне виділення пам'яті. Динамічні масиви. Створення динамічного масиву. 90. Методи внутрішнього сортування. Оцінка кожного з методів. Використання сортування злиттям в якості внутрішнього сортування. 91. Чіткий подання даних у пам'яті. Основні процедури та функції для роботи з ланцюжками. Побудова односпрямованих ланцюжків. Побудова двонаправлених ланцюжків. Основні процедури та функції для роботи з двонаправленими ланцюжками. Теорія програмування 98. Загальна схема програм пошуку по графу. Приклади інтерпретації. 99. Матроіди. Загальна схема і приклади реалізації жадібних алгоритмів. Зв'язок матроіда і жадібних алгоритмів. 100. Принципи і прийоми динамічного програмування. Приклади схем програм реалізації динамічного програмування Література 1. Абель П. Язык ассемблера для IBM PC и программирования. 2. Ахо А., Хопкрофт Д., Ульман Д. Структуры данных и алгоритмы. 3. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. 4. Вирт Д. Алгоритмы и структуры данных. 5. Воеводин В.В. Линейная алгебра. 6. Габасов Р.Ф. Методы оптимизации. 7. Гихман И.И., Скороход А.В., Ядренко М.И. Теория вероятностей и математическая статистика. 8. Дейт К. Ведение в системы баз данных. 9. Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ. 10. Кормен Т., Лайзерсон Ч., Ривест Р., Штайн К., Алгоритмы. Построение и анализ. 11. Крушевский А.В., Теория игр. – К., 1977 – 213 с. 12. Ларичев О.И. Наука и искусство принятия решения. 13. Любимский А.В., Трифонов С.А. Программирование. 14. Матвеев Н.М., Методы интегрирования обыкновенных дифференциальных уравнений. 15. Представление и использование знаний. (Под ред. Х. Уэно, М. Исудзука). 16. Самарский А.А., Гулин А.В. Численные методы. 17. Страуструп Б. Язык программирования C++. 18. Таненбаум Э. Современные операционные системы. 19. Таха X. Введение в исследование операций. 20. Яблонский СВ. Введение в дискретную математику.
Критерії оцінювання знань і вмінь студентів за напрямом прикладна математика В Одеському національному університеті імені І.І. Мечникова розроблено і діє «Положення про кредитно-модульну систему навчання», де визначена рейтингова 100-бальна система оцінки знань та вмінь студентів (РСО). (затверджене Вченою радою 28 квітня 2009 року, протокол № 7). Оцінка – відмінно (А) виставляється студентам, які глибоко й міцно засвоїли програмний матеріал (90-100%), вичерпно, послідовно, грамотно й логічно його викладають, у їх відповідях теорія й практика тісно пов'язані. При цьому студенти без утруднення дають відповідь при видозміненні завдання, творчо застосовують набуті знання, правильно обґрунтовують прийняті рішення, виявляють навички системного підходу до вирішення поставлених завдань. Оцінка – добре (В, С) виставляється студентам, які твердо знають програмний матеріал значно вище середнього рівня (75-89%), грамотно i по суті його викладають, не допускають істотних неточностей у відповідях на запитання, виявляють аналітичні здібності при виконанні завдань, володіють необхідними навичками їх виконання. Оцінка – задовільно (D, E) виставляється студентам, які викладають матеріал достатньо послідовно, однак виявляють знання тільки основного програмного матеріалу (60-74%), допускають окремі неточності, не досить правильні формулювання при викладі програмного матеріалу, одночасно володіють умінням виконання поставлених завдань. Оцінка – незадовільно (FX) виставляється студентам, які не знають значної частини програмного матеріалу (30-59%), викладають його не послідовно, допускають істотні помилки, невпевнено, із великими утрудненнями виконують поставленні завдання. Оцінка – незадовільно (F) виставляється студентам, які не знають переважну частини програмного матеріалу (0-29%), не здатні викласти його.
Переведення підсумкових рейтингових оцінок виражених у балах за багатобальною шкалою, в оцінки за національною шкалою та шкалою ЄКТС здійснюється відповідно до таблиці Таблиця. – Розподіл балів за національною шкалою та шкалою ЄСПК
Розглянуто „16” березня 2015 р. на засіданні навчально-методичної комісії з математики
Голова комісії ______ Вартанян Г. М.
Затверджено на засіданні Вченої Ради ІМЕМ. Протокол № 3 від „17” березня 2015 р.
Вчений секретар ст.викл. Білозерова М.О.
Математичний аналіз 1. Межа функції (визначення по Коші і по Гейне). Визначення безперервності функції в точці. Теореми Вейєрштрасса і Больцано - Коші про функції, безперервних на відрізку. Рівномірна неперервність, теорема Кантора. 2. Дифференційованіть і похідна дійсної функції дійсного змінного. Геометричний зміст похідної. Основні теореми про диференційовні функції (теореми Ферма, Ролля, Лагранжа). Формула Тейлора із залишком у формі Пеано, у формі Лагранжа. 3. Визначення інтеграла Рімана. Інтегровність монотонних і безперервних функцій. Існування первісної у безперервної функції. Формула Ньютона - Лейбніца. 4. Числові ряди. Основні ознаки збіжності (ознака порівняння, Даламбера. Коші, інтегральна ознака) для рядів з невід'ємними членами. Ознака Лейбніца. Поняття абсолютної та умовної збіжності. Диференціальні рівняння 5. Задача Коші для диференціального рівняння першого порядку. Теорема існування та єдиності розв'язку задачі Коші. 6. Лінійні однорідні звичайні диференціальні рівняння n-го порядку з постійними коефіцієнтами. Метод Ейлера. 7. Лінійні неоднорідні звичайні диференціальні рівняння n-го порядку з постійними коефіцієнтами. метод Лагранжа Рівняння математичної фізики 8. Формулювання крайової задачі Штурма-Ліувілля. Звести задачу Штурма-Ліувілля до інтегрального рівняння. 9. Властивості власних значень і власних функцій задачі Штурма-Ліувілля. Довести теорему розкладання Стеклова. 10. Функція Гріна одновимірної крайової задачі. (В чому відмінність від фундаментальної функції). Довести теорему єдиності для функції Гріна 11. Дати визначення самосопряженної крайової задачі. Довести симетричність функції Гріна для самосопряженної крайової задачі. 12. Дати визначення фундаментальної та базисної систем рішень для одновимірної крайової задачі. Довести теорему існування для функції Гріна. Теорія ймовірностей 13. Дискретне простір елементарних подій. Операції над подіями. Класичне визначення ймовірності. Властивості ймовірності. 14. Умовні ймовірності. Незалежні події та їх властивості. 15. Випадкові величини. Функція розподілу випадкової величини та її властивості. 16. Числові характеристики випадкових величин: математичне сподівання, дисперсія та їх властивості. 17. Ланцюги Маркова. Матриці переходу за один і к-кроків для однорідного ланцюга Маркова. Функціональний аналіз 18. Лінійні оператори в лінійних нормованих просторах. Лінійне простір лінійних операторів (обмежених) 19. Абстрактні ряди Фурьє в Н. Теорема Рисса – Фішера. Теорема Гіильберта – Шмидта Аналіз данних 20. Інформаційні та аналітичні моделі. Учасники процесу аналізу даних. Формалізація даних. Основні етапи KDD. Класи задач, що вирішуються методами Data Mining 21. Алгоритми Data Mining - асоціативні правила. Характеристики значущості асоціативного правила 22. Аналіз рядів динамік. моделі прогнозування. Випадкові процеси 23. Випадкові процеси марківського типу. Рівняння Колмогорова. 24. Процеси не залежать від майбутнього. Теорема Колмогорова-Прохорова. Тотожність Вальда. 25. Коваріація та кореляція випадкового процесу. Взаємна коваріаційна і кореляційна функції випадкових процесів Похідна та інтеграл від випадкового процесу
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-24; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.37.85 (0.007 с.) |

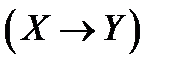 .
.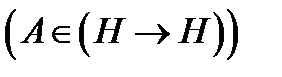 .
.


