
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначники 2-го і 3-го порядківСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Визначники 2-го і 3-го порядків Визначником матриці другого порядку називається число, яке розраховується за формулою Визначником матриці третього порядку називається число, яке обчислюється за формулою
За допомогою схеми можна запам'ятати формулу обчислення визначника третього порядку: визначник складається із шести доданків, кожен доданок формули являє собою добуток трьох елементів матриці, вибраних по одному з кожного рядка та кожного стовпчика та позначених на схемі однаковим кольором. Зі знаком "+" беруться три добутки, отримані з лівого малюнку, зі знаком - отримані з правого малюнку. Таке правило обчислення визначників третього порядку називається правилом трикутників.
Правило Крамера Метод Крамера (Крамера правило) — спосіб розв'язання квадратних систем лінійних алгебраїчних рівнянь із ненульовим визначником основної матриці (при цьому для таких рівнянь розв'язок існує і є єдиним). Метод було створено Габріелем Крамером у 1750 році. Для системи n лінійних рівнянь з n невідомими (над довільним полем)
з визначником матриці системи
(i-й стовпчик матриці системи замінюється стовпчиком вільних членів).
У такій формі формула Крамера справедлива без припущення, що
Властивості визначників. 1.Визначник не змінюється при транспонуванні матриці. Отже при обчисленні визначника його рядки та стовпчики є рівноправними. 2. Якщо визначник містить нульовий рядок (стовпчик), то він дорівнює нулю. 3.Якщо всі елементи рядка (стовпчика) визначника мають спільний множник, то цей множник можна винести за знак визначника. 4. При перестановці двох довільних рядків (стовпчиків) визначника, визначник змінює знак на протилежний. 5. Якщо визначник містить два однакових рядки (стовпчики), то він дорівнює нулю.
6. Якщо визначник містить два пропорційних рядки (стовпчики), то він дорівнює нулю. 7. Сума добутків елементів одного рядка (стовпчика) визначника на алгебраїчні доповнення до елементів іншого рядка (стовпчика) цього визначника дорівнює нулю. 8. Визначник добутку матриць дорівнює добутку визначників цих матриць: 9. Визначник не зміниться, якщо до елементів довільного його рядка (стовпчика) додати відповідні елементи іншого його рядка (стовпчика), помножені на довільне число. Зауваження. Остання властивість використовується для спрощення елементів визначника перед використанням теореми Лапласа. Лінійна залежність векторів. Набір векторів Набір векторів Властивості лінійно залежних та лінійно незалежних наборів векторів. 1. Якщо набір векторів містить нульовий вектор, то цей набір - лінійно залежний. 2. Якщо набір векторів містить лінійно залежну підсистему, то весь набір - лінійно залежний. 3. Якщо набір векторів лінійно незалежний, то будь-яка його підсистема - лінійно незалежна. На практиці для перевірки лінійної залежності або незалежності набору векторів використовують таку схему, яку ми проілюструємо на прикладі.
Ранг матриці. Мінором порядку k, що побудований за елементами матриці, називається визначник, складений з її елементів, що розташовані на перетині k її фіксованих рядків та k фіксованих стовпчиків. Рангом матриці А називається порядок максимального ненульо-вого мінору, що побудований за її елементами, а будь-який такий мінор називається базисним мінором матриці та позначається Мб. Зауважимо, що у матриці А базисний мінор може бути не один. Ранг матриці А позначається через r(А). З означення випливає: 1) 0 ≤ r(А) ≤ min {m, n}; 2) r(А) = 0 <=> А = 0 (тобто матриця А - нульова); 3) якщо матриця А - квадратна порядку n, то r (А) = n <=> |А| ≠ 0.
Системи лінійних рівнянь. Система т лінійних рівнянь із п невідомими записується у вигляді:
Де x1, x2,…, xn невідомі системи, aij - коефіцієнт при невідомій xj в і-му рівнянні, bi, - вільний коефіцієнт в і-му рівнянні. Матрицею СЛР називається матриця коефіцієнтів при невідомих, тобто
Вектором, невідомих називається вектор Розширеною матрицею СЛР називається матриця
Очевидно, між системами лінійних трицями існує взаємно однозначна відповідність (тобто за системою однозначно виписується розширена матриця, та за розширеною матрицею однозначно виписується система). За допомогою введених понять СЛР можна подати у такому матричному вигляді: Тут ліва частина є матричним добутком матриці А розмірності тхn та матриці-стовпчика Очевидно, виконуючи операцію множення матриць, отримаємо початкову СЛР. Однорідною називається система лінійних рівнянь, що має нульовий стовпчик вільних членів, Неоднорідною називається система лінійних рівнянь, хоча б один елемент стовпчика вільних членів якої є ненульовим. Розв'язком, системи лінійних рівнянь, що містить n невідомих, називається впорядкований набір з n дійсних чисел - n-вимірний вектор За множиною розв'язків системи поділяють на такі види. Система лінійних рівнянь називається сумісною, якщо має хоча б один розв'язок, та несумісною, якщо розв'язків не має. Сумісна система лінійних рівнянь називається визначеною, якщо має єдиний розв'язок, та невизначеною, якщо розв'язків більше одного. Зауваження. Очевидно, однорідна СЛР завжди сумісна, оскільки нульовий вектор завжди є її розв'язком. Алгоритм методу. І етап (прямий хід методу): кількість кроків збігається з кількістю змінних системи (стовпчиків матриці системи). й крок. Виключаємо змінну х1 з усіх рівнянь, крім першого. Для цього в першому стовпчику розширеної матриці шукають ненульовий (ведучий) елемент, переставляють його рядок на перше місце та за допомогою елементарних перетворень над всіма наступними рядками та цим фіксованим роблять нулі під ведучим елементом. 1- й крок. Виключаємо змінну х2 з усіх рівнянь, крім перших двох. Для цього у другому стовпчику отриманої матриці, починаючи з другого місця, шукають ненульовий (ведучий) елемент. Якщо такий є: переставляють його рядок на друге місце та за допомогою елементарних перетворень над всіма наступними рядками та цим фіксованим роблять нулі під ведучим елементом. Якщо такого немає, змінну х2 вважають вільною. к -й крок. У к- му стовпчику попередньої матриці шукають ненульовий (ведучий) елемент. Якщо попередня змінна вільна, то з того ж місця, що й на попередньому кроці. Інакше - з наступного місця. Якщо такий елемент є: переставляють його рядок на те місце, починаючи з якого шукали ведучий елемент, та за допомогою елементарних перетворень над всіма наступними рядками та цим фіксованим роблять нулі під ведучим елементом. Якщо такого немає, змінну хк вважають вільною. Таким чином, проходимо всі стовпчики матриці системи А. Після чого матриця набуває східчастого вигляду. II етап. Аналіз множини розв'язків СЛР. Якщо остання матриця І етапу містить нульовий рядок, якому відповідає ненульовий вільний член, то СЛР - несумісна, оскільки такий рядок відповідає рівнянню 0∙X1+ 0∙X2+...+ 0∙Xn = b, Ь ≠ 0. У протилежному випадку СЛР - сумісна.
Для сумісної СЛР: якщо вона містить вільні змінні, то система невизначена, інакше система визначена. Ш етап. Зворотній хід методу (виконується лише для сумісних СЛР). 1. За останньою матрицею перетворень І етапу виписується відповідна СЛР (еквівалентна початковій за теоремою). 2. Надаючи вільним змінним (якщо такі є) довільних значень, їх переносять у праву частину кожного рівняння (матриця з базисних змінних стає верхньотрикутною, отже невиродженою). 3. Починаючи з останнього рівняння, знаходять відповідні значення базисних змінних. 4. Виписується розв'язок СЛР (у вигляді вектора).
Обернена матриця Нагадаємо, що оберненою до матриці А називається матриця А-1, яка задовольняє співвідношення А-1∙А = А∙А-1 = Е, де Е - одинична матриця, обернена матриця може існувати лише для квадратних матриць, але не кожна квадратна матриця має обернену. Якщо визначник матриці А не дорівнює нулю, ця матриця називається невиродженою, інакше матриця А називається виродженою. Теорема (необхідна та достатня умова існування оберненої матриці). Обернена до матриці А матриця
Границя функції. Нехай функція Визначення 1. (Гейне ). Число Якщо число A– границя функції в точці Нехай функція Визначення 2. (Коші). Число A називається границею функції
виконується нерівність
Визначення границі функції в точці за Гейне і за Коші еквівалентні.
Неперервність функції
Точки розриву
Похідна функції. Похідною функції
Похідна може позначатись
Правила диференціювання Нехай функції 1. Похідна від суми (різниці) двох функцій: 2. Похідна від добутку двох функцій: 3. Похідна від частки двох функцій: 4. Похідна складної функції: якщо
17.Таблиця похідних
Диференціал
19.Похідні вищих порядків, диференціали. Нехай функція у = f(х) визначена та має похідну першого порядку на інтервалі (а,Ь). Тоді її похідна у' = f '(х) також буде функцією, що визначена на інтервалі (а,Ь). Якщо ця функція сама є диференційованою в деякій точці х інтервалу (а,Ь), тобто має в цій точці похідну, то вказана похідна називається другою похідною або похідною 2-го порядку і позначається
Аналогічно можна ввести поняття третьої похідної, потім четвертої і т.д. Похідною п-го порядку називається похідна від похідної (n-І)-го порядку і позначається
Правило Лопіталя Правило Лопіталя для розкриття невизначеностей типу
Приклади
Правило Лопіталя може застосовуватись послідовно декілька разів, якщо відношення похідних знову приводить до невизначеності, а самі похідні задовольняють умовам застосування правила Лопіталя.
Розкриття невизначеностей типу 0∙∞ і ∞-∞ проводять за допомогою тотожних перетворень, що приводять ці невизначеності до ви гляду
Розкриття невизначеностей типу ∞0, 00, 1∞ проводять із попереднім перетворенням степенево-показникового виразу за основною логарифмічною тотожністю У результаті цих дій отримаємо (формальний запис):
Екстремум функції. Функція f(х) називається зростаючою на інтервалі (а, Ь), якщо Якщо при Якщо Точка х0 називається точкою локального максимуму (мінімуму) функції у = f(х), якщо функції в деякому околі цієї точки. Точки локального максимуму і мінімуму функції називаються точками екстремуму цієї функції.
Функції багатьох змінних. Як відомо, будь-який упорядкований набір з n дійсних чисел х1…,хn позначається (х1,…,хn) або М(х1,…,хn) і називається точкою n -вимірного арифметичного простору Rn; числа х1,…,хn називаються координатами точки М(х1,…,хn). Відстань між точками М(х1,…,хn) і М/(х/1,…,х/n) визначається за формулою Нехай D
яка визначає, взагалі кажучи, деяку поверхню в R3. Нехай (х01,…,х0k,…x0n) – довільна фіксована точка в області визначення функції u = f(х1,…,хn). Надаючи значенню змінної хk приросту
Ця границя називається частинною похідною 1-го порядку функції по змінній xk в точці (x01,…,x0n) і позначається
Аналогічно визначаються і позначаються частинні похідні порядку вищого, ніж другий. Функція u=f(M) називається диференційовною в точці М0, якщо скрізь в околі цієї точки певний приріст функції можна подати у вигляді
де Диференціалом 1-го порядку du функції Диференціал k -го порядку функції яка формально розкривається за біномним законом. Градієнт функції Прикладом функцій багатьох змінних в економіці э виробничі функції
Частинні похідні
Умовний екстремум
32. Найбільше та найменше значення функції в замкненій області
33. Первісна функція та невизначений інтеграл
Таблиця інтегралів
35. Основні методи інтегрування: метод підстановки, інтегрування частинами
36. Інтегрування раціональних дробів
Визначений інтеграл Означення: Якщо існує скінченна границя інтегральних сум Sn при lіà0 і не залежить ні від способу розбиття [a;b] на частини Dхі, ні від вибору точок xі, то ця границя називається визначеним інтегралом від ф-ії f(x) на проміжку [a;b] і позначається:
За означенням, визначений інтеграл Ф-ія, для якої на інтервалі існує визначений інтеграл називається інтегровною. Формула Ньютона-Лейбніца Теорема (Ньютона-Лейбніца): Якщо ф-ія f(x) – неперервна для xÎ [a;b], то визначений інтеграл від ф-ії f(x) на проміжку [a;b] дорівнює приросту первісної ф-ії f(x) на цьому проміжку, тобто:
Зв’язок між визначеним та невизначеним інтегралами можна представити такою рівністю:
Невласні інтеграли Нехай f(x) інтегровна для будь-якого скінченного b Î[a;+¥), так що Означення: Границя
Якщо ця границя скінченна, то невластивий інтеграл називається збіжним, а якщо не існує (в тому числі нескінченна), – розбіжним. Вважаючи, що f(x) – інтегровна для скінченних a та b, формули для обчислення невластивих інтегралів на нескінченному проміжку мають вигляд:
де с=const. Теорема: Якщо при x ³ a має місце нерівність 0£f(x)£g(x) то із збіжності інтеграла Метод Бернуллі За методом Бернуллі шукають загальний розв’язок лінійного неоднорідного рівняння у вигляді
Шукають Необхідна ознака збіжності. Теорема: Якщо ряд
збіжний, то:
Доведення: Оскільки ряд збіжний, то:
поряд з цією рівністю для збіжного ряду можна записати:
Ця ознака є лише необхідною умовою збіжності. Якщо вона не виконується, то ряд розбіжний, якщо виконується, то ряд може бути як збіжним, так і розбіжним. Функціональні ряди. Означення: Ряд вигляду U1(x)+U2(x)+…+Un(x)+…, де членами рядуUn(x) є ф-ції від аргументу х, називається функціональним рядом. При х=х0 функціональний ряд перетворюється на на числовий ряд. Означення: Всі значення аргументу х, при яких функціональний ряд збігається, називаються областю збіжності функціонального ряду. Степеневі ряди: Означення: Функціональний ряд вигляду a0+a1x+a2x2+…+anxn+… називається степеневим рядом, його загальний член Un(x)=anxn, а числа а0,а1,а2,...,аn,... – називають коефіцієнтами степеневого ряду. Степеневий ряд можна записати як:
Степеневий ряд може мати вигляд: a0+a1(x-с)+a2(x-с)2+…+an(x-с)n+… Такий ряд за допомогою заміни х-с=у зводиться до звичайного степеневого ряду.
51. Знакозмінні ряди.
Функціональні ряди. Вираз Ознака Вайєрштраса. Функціональний ряд вигляду Теорема Абеля. Якщо степеневий ряд збігається в точці Число радіус збіжності визначається за формулою
53. Степеневі ряди.
Визначники 2-го і 3-го порядків Визначником матриці другого порядку називається число, яке розраховується за формулою Визначником матриці третього порядку називається число, яке обчислюється за формулою
За допомогою схеми можна запам'ятати формулу обчислення визначника третього порядку: визначник складається із шести доданків, кожен доданок формули являє собою добуток трьох елементів матриці, вибраних по одному з кожного рядка та кожного стовпчика та позначених на схемі однаковим кольором. Зі знаком "+" беруться три добутки, отримані з лівого малюнку, зі знаком - отримані з правого малюнку. Таке правило обчислення визначників третього порядку називається правилом трикутників.
Правило Крамера Метод Крамера (Крамера правило) — спосіб розв'язання квадратних систем лінійних алгебраїчних рівнянь із ненульовим визначником основної матриці (при цьому для таких рівнянь розв'язок існує і є єдиним). Метод було створено Габріелем Крамером у 1750 році. Для системи n лінійних рівнянь з n невідомими (над довільним полем)
з визначником матриці системи
(i-й стовпчик матриці системи замінюється стовпчиком вільних членів).
У такій формі формула Крамера справедлива без припущення, що
Властивості визначників. 1.Визначник не змінюється при транспонуванні матриці. Отже при обчисленні визначника його рядки та стовпчики є рівноправними. 2. Якщо визначник містить нульовий рядок (стовпчик), то він дорівнює нулю. 3.Якщо всі елементи рядка (стовпчика) визначника мають спільний множник, то цей множник можна винести за знак визначника. 4. При перестановці двох довільних рядків (стовпчиків) визначника, визначник змінює знак на протилежний. 5. Якщо визначник містить два однакових рядки (стовпчики), то він дорівнює нулю. 6. Якщо визначник містить два пропорційних рядки (стовпчики), то він дорівнює нулю. 7. Сума добутків елементів одного рядка (стовпчика) визначника на алгебраїчні доповнення до елементів іншого рядка (стовпчика) цього визначника дорівнює нулю. 8. Ви
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 4092; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.184.76 (0.015 с.) |


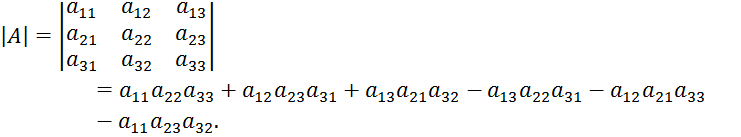

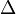 , що не рівний нулю, розв'язок записується у такому вигляді:
, що не рівний нулю, розв'язок записується у такому вигляді: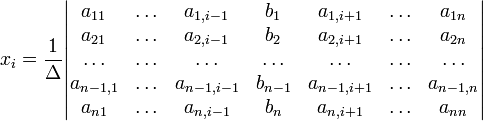

 та
та  , або набір
, або набір 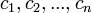 складаються не з елементів кільця коефіциєнтів системи, а деякого модуля над цим кільцем.
складаються не з елементів кільця коефіциєнтів системи, а деякого модуля над цим кільцем. . З цієї властивості слідує, що хоча A∙B≠B∙A, але
. З цієї властивості слідує, що хоча A∙B≠B∙A, але 
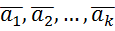 називається лінійно незалежним, якщо
називається лінійно незалежним, якщо  , та лінійно залежним, якщо
, та лінійно залежним, якщо  , де не всі числа
, де не всі числа  дорівнюють нулю.
дорівнюють нулю.
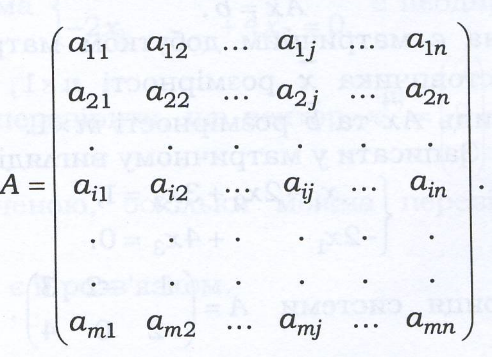
 , вектором вільних членів називається вектор
, вектором вільних членів називається вектор 


 розмірності n х 1, а рівність означає рівність двох матриць
розмірності n х 1, а рівність означає рівність двох матриць  розмірності т х 1.
розмірності т х 1.
 де матриця
де матриця  складається з алгебраїчних доповнень до кожного елементу матриці АT і називається приєднаною.
складається з алгебраїчних доповнень до кожного елементу матриці АT і називається приєднаною. визначена на деякій підмножині
визначена на деякій підмножині  множини дійсних чисел
множини дійсних чисел  ,і
,і 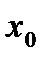 – гранична точка множини
– гранична точка множини 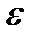 –околі
–околі  граничної точки
граничної точки  називається границею функції
називається границею функції  при
при  (або в точці
(або в точці  , збіжної до
, збіжної до  збіжна до
збіжна до  .
. або
або  при
при  має границю
має границю  при
при  (або в точці
(або в точці 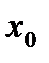 ), якщо для будь-якого
), якщо для будь-якого  можна знайти таке число
можна знайти таке число  , що при всіх
, що при всіх  , які задовольняють нерівність
, які задовольняють нерівність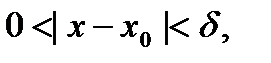

 Друга чудова границя та її наслідки.
Друга чудова границя та її наслідки.



 в точці
в точці  називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.
називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.

 мають у певній точці
мають у певній точці  похідні
похідні 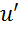 ,
, 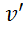 .
.



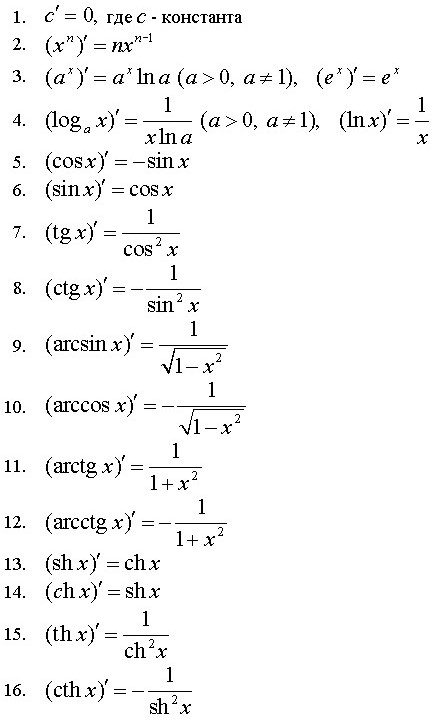

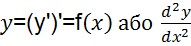 .
.

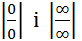 полягає в такому: якщо функції f(х) і g(х) нескінченно малі або нескінченно великі при х → а, диференційовані в околі точки х=а,g(x)≠0в околі цієї точки, існує
полягає в такому: якщо функції f(х) і g(х) нескінченно малі або нескінченно великі при х → а, диференційовані в околі точки х=а,g(x)≠0в околі цієї точки, існує  , то існує
, то існує 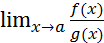 і справедлива рівність
і справедлива рівність
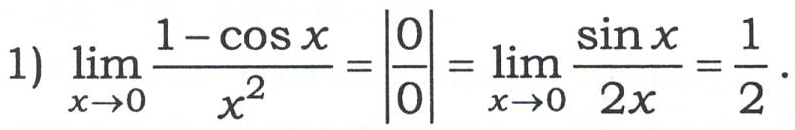
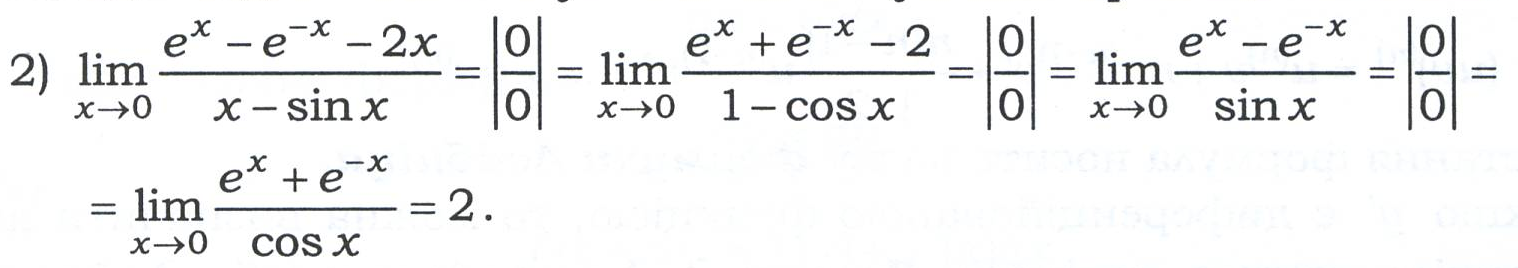
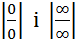 , а потім застосовують таблицю еквівалентних нескінченно малих величин і правило Лопіталя.
, а потім застосовують таблицю еквівалентних нескінченно малих величин і правило Лопіталя.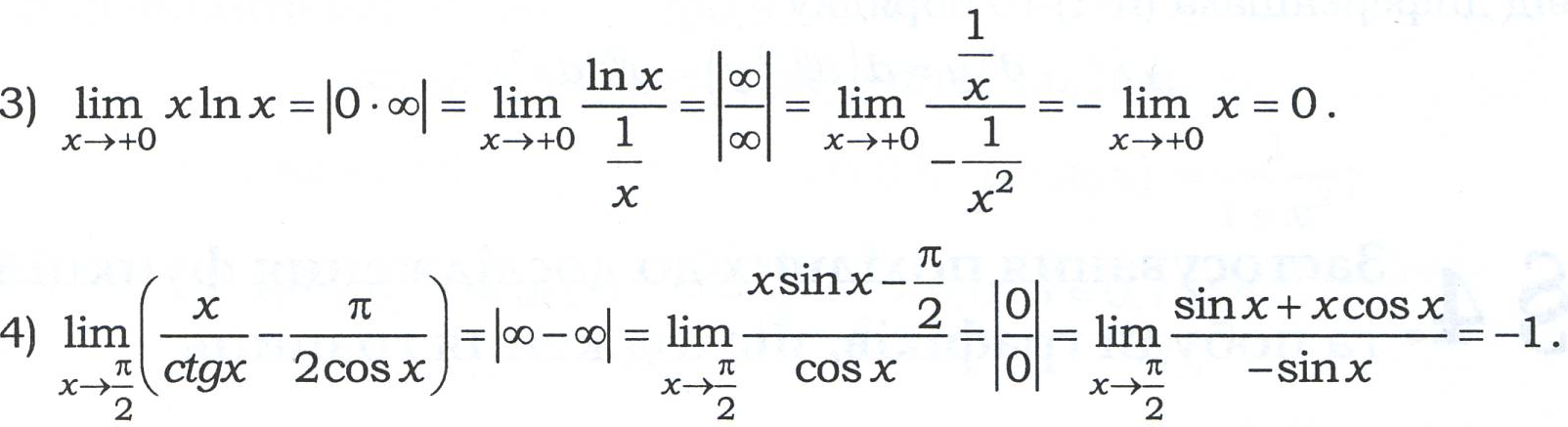
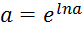
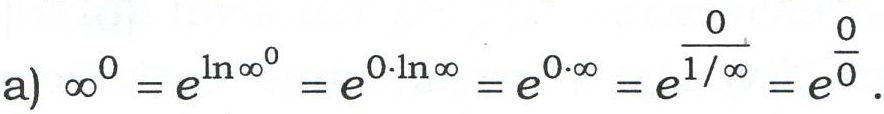
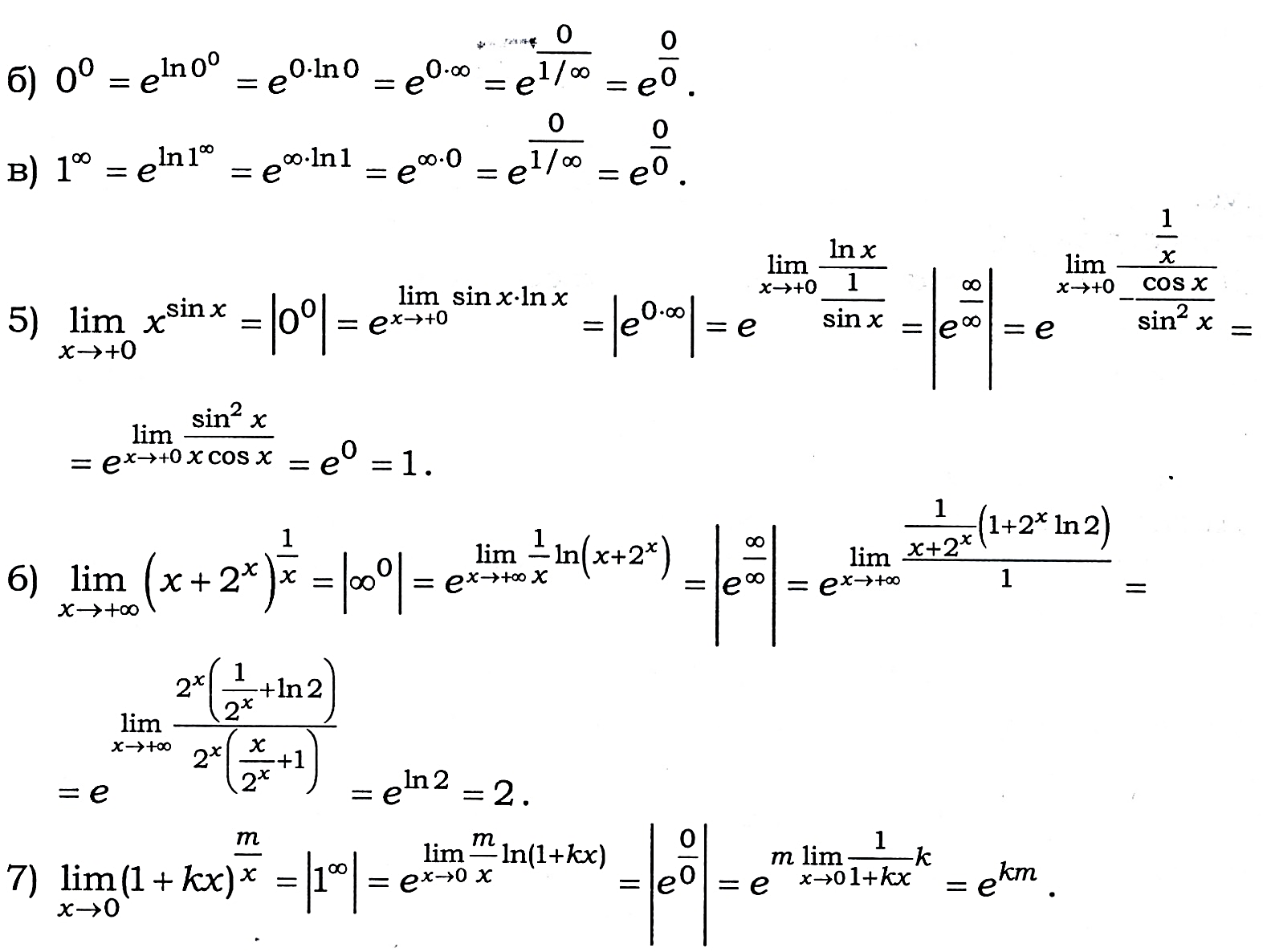
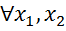 зцього інтервалу, таких, що
зцього інтервалу, таких, що 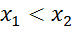 , виконується умова
, виконується умова 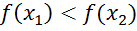 .
. , то функція називається спадною.
, то функція називається спадною. на (а,Ь), то функція на цьому інтервалі зростає. Якщо
на (а,Ь), то функція на цьому інтервалі зростає. Якщо 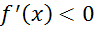 на (а,Ь), то функція на цьому інтервалі спадає.
на (а,Ь), то функція на цьому інтервалі спадає.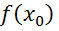 є найбільшим (найменшим) значенням
є найбільшим (найменшим) значенням
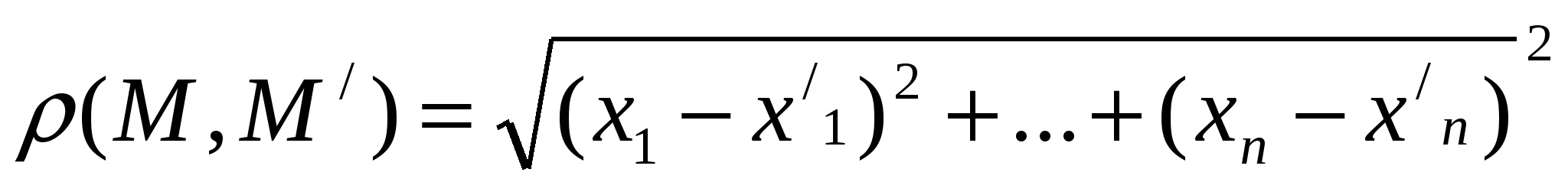
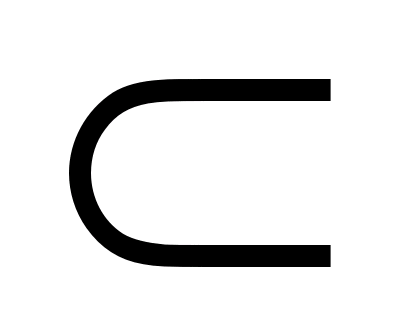 Rn – довільна множина n -вимірного арифметичного простору. Якщо кожній точці М(х1,…,хn)
Rn – довільна множина n -вимірного арифметичного простору. Якщо кожній точці М(х1,…,хn)  D поставлено у відповідність деяке цілком визначене дійсне число f(M)= f(х1,…,хn), то кажуть, що на множині D задана числова функція f: Rn
D поставлено у відповідність деяке цілком визначене дійсне число f(M)= f(х1,…,хn), то кажуть, що на множині D задана числова функція f: Rn  R від n змінних х1…,хn. Множина D називається областю визначення, а множина
R від n змінних х1…,хn. Множина D називається областю визначення, а множина  - множиною значень функції f. Зокрема, при n = 2 функцію двох змінних z = f(x,y),(x,y)
- множиною значень функції f. Зокрема, при n = 2 функцію двох змінних z = f(x,y),(x,y) 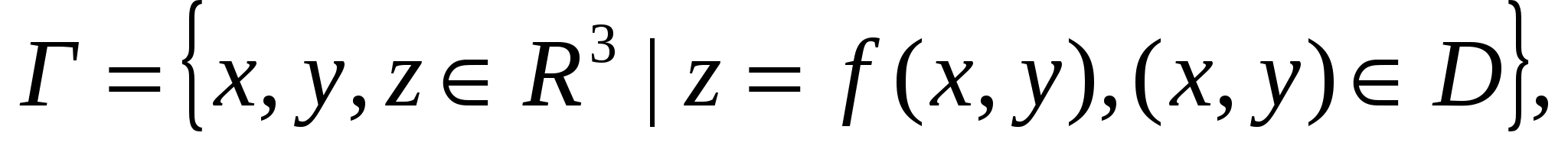
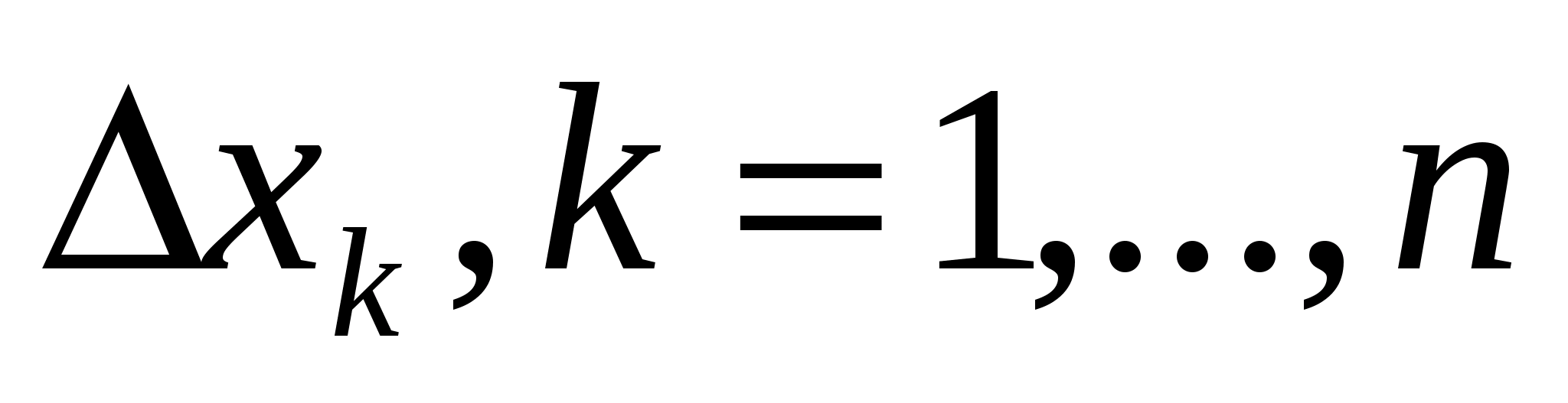 , розглянемо границю
, розглянемо границю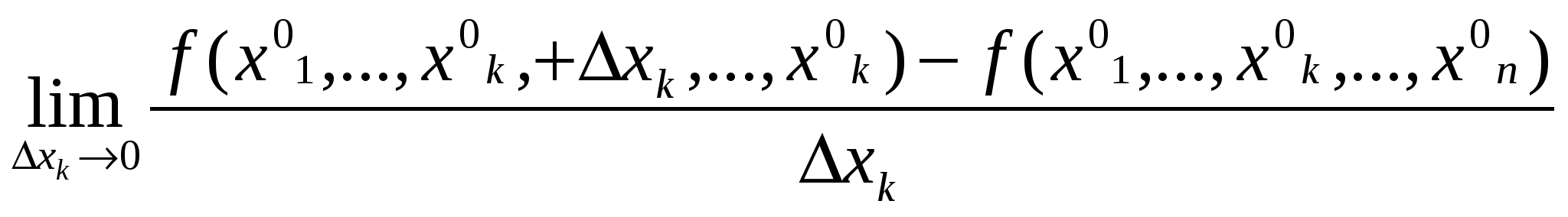 .
.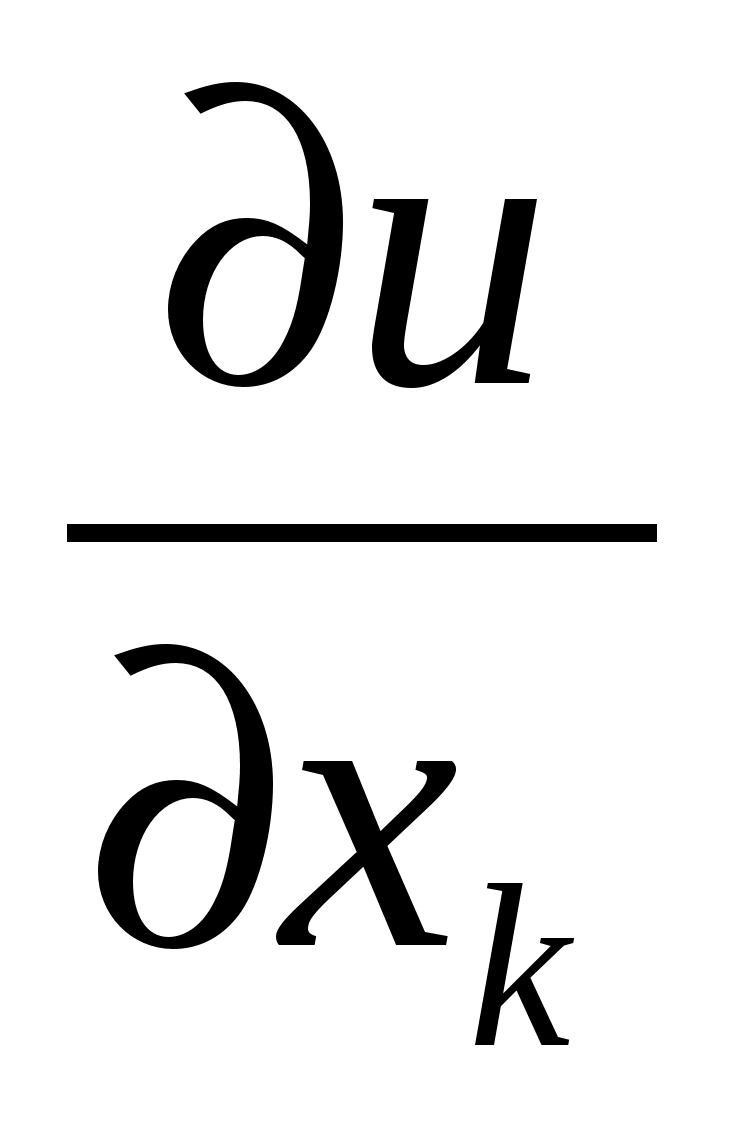 або
або  Похідні другого порядку позначаються так:
Похідні другого порядку позначаються так: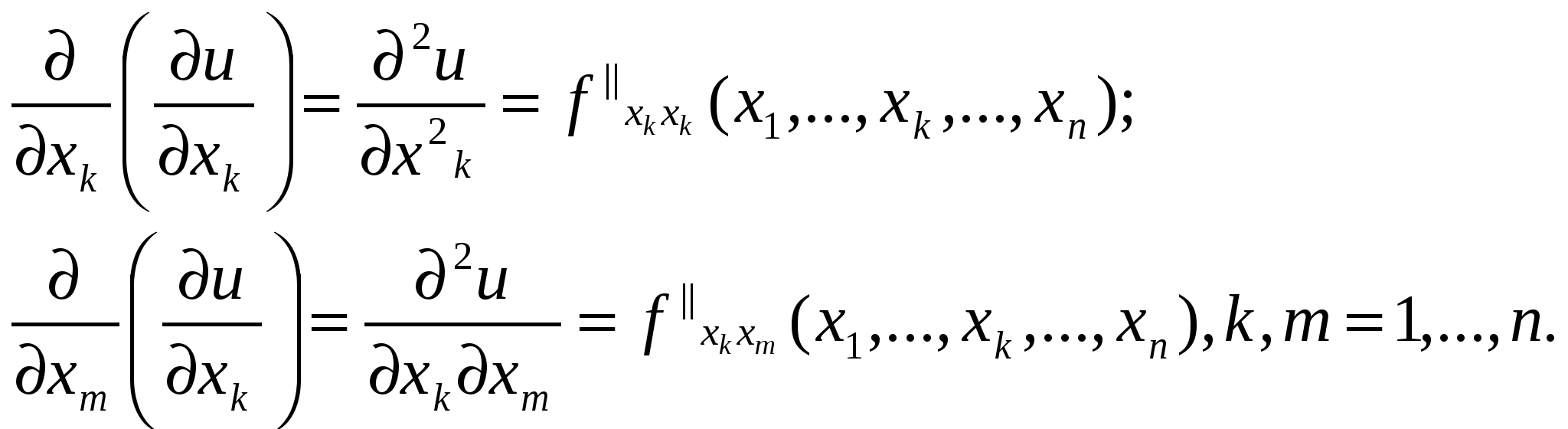
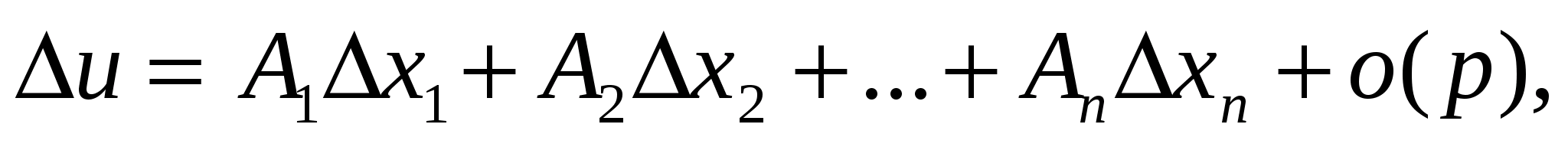
 A1,…An – числа, не залежні від
A1,…An – числа, не залежні від  .
.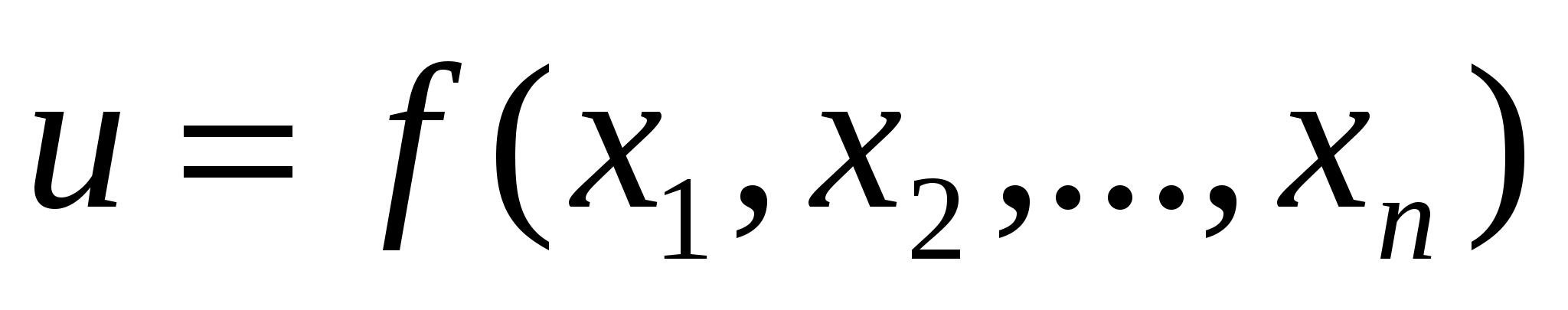 називається вираз
називається вираз 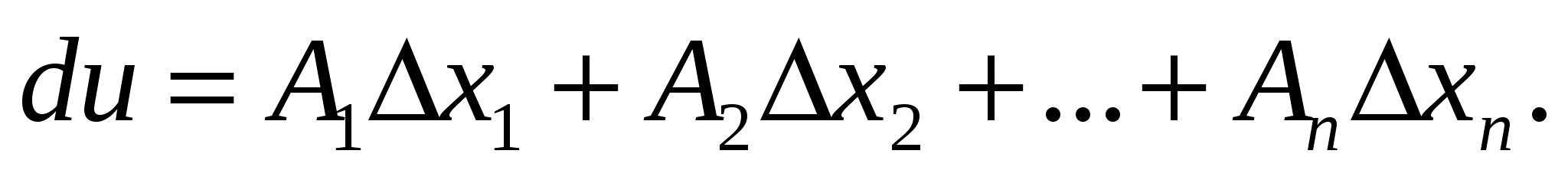
 , де х1…хn – незалежні змінні, символічно записуються у вигляді формули
, де х1…хn – незалежні змінні, символічно записуються у вигляді формули 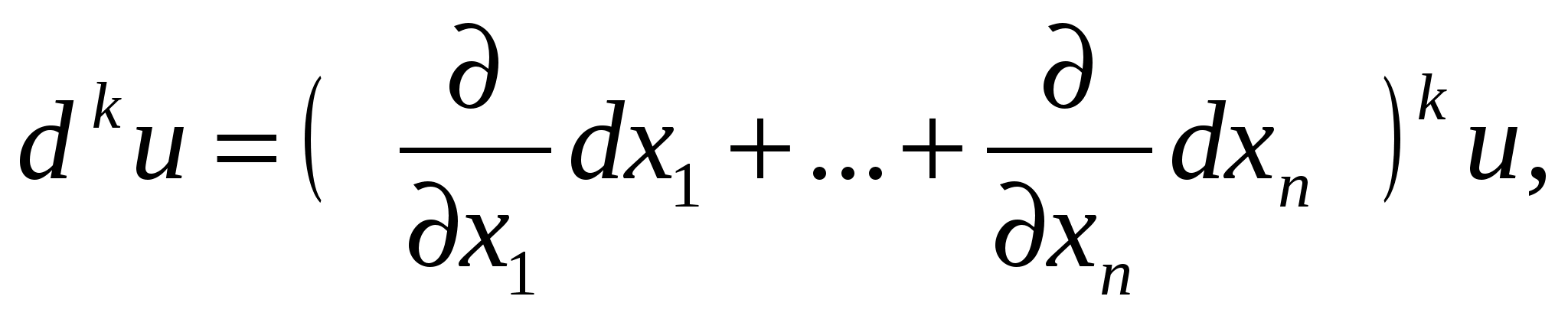
 - це вектор, що визначається формулою grad
- це вектор, що визначається формулою grad 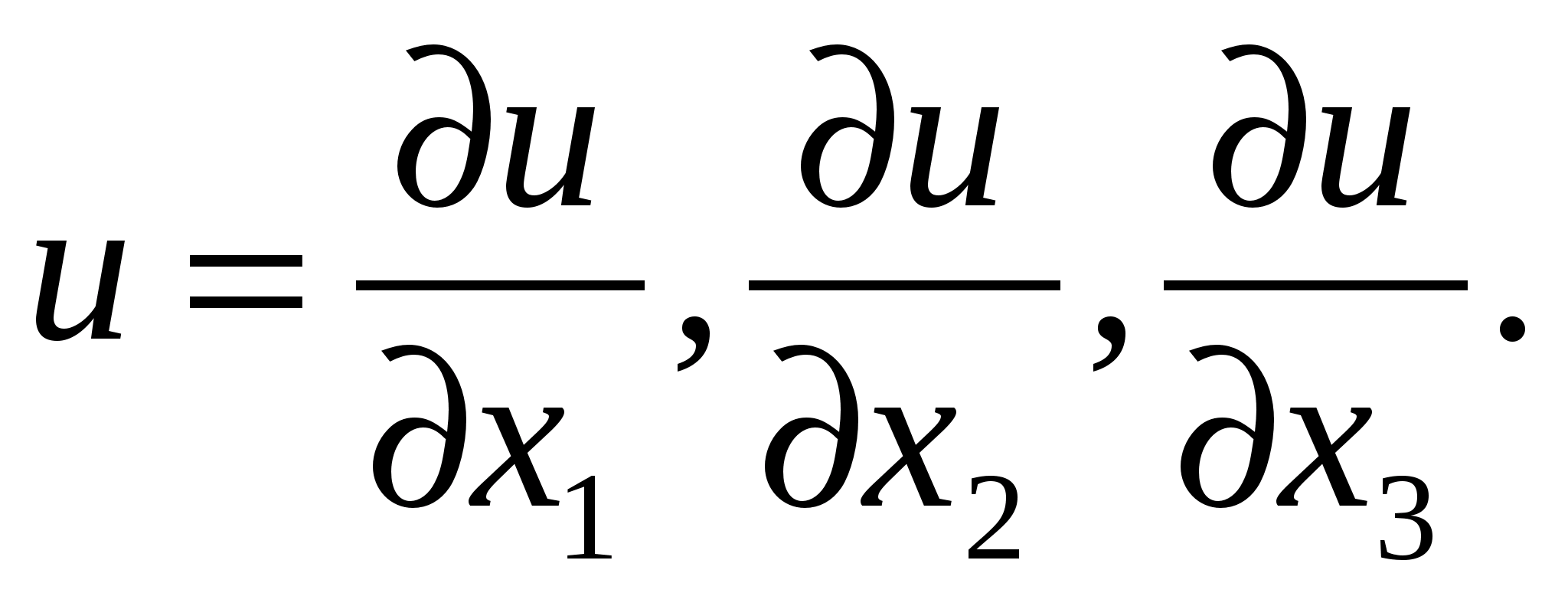 Він визначає напрямок найшвидшого зростання функції
Він визначає напрямок найшвидшого зростання функції














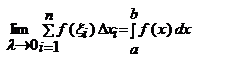
 – число, яке залежить від типу ф-ії f(x) та проміжку [a;b]; він не залежить від того, якою буквою позначена змінна інтегрування. Визначений інтеграл — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. Визначений інтеграл є неперервним функціоналом, лінійним по підінтегральним функціям і адитивним по області інтегрування. У найпростішому випадку область інтегрування — це відрізок числової осі. Геометричний зміст визначеного інтеграла — це площа криволінійної фігури (криволінійної трапеції), обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції.
– число, яке залежить від типу ф-ії f(x) та проміжку [a;b]; він не залежить від того, якою буквою позначена змінна інтегрування. Визначений інтеграл — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. Визначений інтеграл є неперервним функціоналом, лінійним по підінтегральним функціям і адитивним по області інтегрування. У найпростішому випадку область інтегрування — це відрізок числової осі. Геометричний зміст визначеного інтеграла — це площа криволінійної фігури (криволінійної трапеції), обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції. де F’(x)=f(x)
де F’(x)=f(x)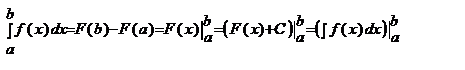 Наслідок: Для обчислення визначеного інтеграла достатньо знайти одну із первісних підінтегральної ф-ії і виконати над нею подвійну підстановку.
Наслідок: Для обчислення визначеного інтеграла достатньо знайти одну із первісних підінтегральної ф-ії і виконати над нею подвійну підстановку. існує.
існує.

 виходить збіжність інтеграла
виходить збіжність інтеграла  , або із розбіжності
, або із розбіжності  випливає розбіжність
випливає розбіжність  .
. , де
, де  - невідомі диференційовані функції. Враховуючи співвідношення
- невідомі диференційовані функції. Враховуючи співвідношення  , рівняння
, рівняння  перетворюється у наступне:
перетворюється у наступне: 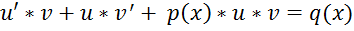 , звідки
, звідки ,(1)
,(1) як розв’язок рівняння з відокремленими змінними
як розв’язок рівняння з відокремленими змінними  , звідки
, звідки  . Обирають значення довільної сталої
. Обирають значення довільної сталої  та повертаються до рівняння (1), підставивши в нього знайдену функцію
та повертаються до рівняння (1), підставивши в нього знайдену функцію  , звідки
, звідки  . Остаточно, враховуючи
. Остаточно, враховуючи 
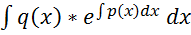 .
.







 називається функціональним рядом. Приклад
називається функціональним рядом. Приклад  При одних значеннях
При одних значеннях  ряд може сходитися, для інших значень - розходитися.При кожному конкретному значенні
ряд може сходитися, для інших значень - розходитися.При кожному конкретному значенні  із області визначення D функціональний ряд перетворюється на числовий. Якщо для
із області визначення D функціональний ряд перетворюється на числовий. Якщо для  є D числовий ряд
є D числовий ряд  збігається, то кажуть, що функціональний ряд збігається в точці
збігається, то кажуть, що функціональний ряд збігається в точці  абсолютно і рівномірно збіжний на проміжк
абсолютно і рівномірно збіжний на проміжк  , якщо існує знакододатний збіжний числовий ряд
, якщо існує знакододатний збіжний числовий ряд  такий, що для всіх
такий, що для всіх 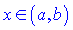 виконується умова
виконується умова 
 , то він збігається абсолютно в інтервалі
, то він збігається абсолютно в інтервалі  Якщо степеневий ряд розбіжний в точці
Якщо степеневий ряд розбіжний в точці 
 називають радіусом збіжності степеневого ряду, а проміжок
називають радіусом збіжності степеневого ряду, а проміжок  - інтервалом збіжності (областю збіжності).Якщо всі коефіцієнти ряду ненульові, то радіус збіжності рівний наступній границі
- інтервалом збіжності (областю збіжності).Якщо всі коефіцієнти ряду ненульові, то радіус збіжності рівний наступній границі  при умові, що вона існує (скінченна чи нескінченна).Для рядів вигляду
при умові, що вона існує (скінченна чи нескінченна).Для рядів вигляду 
 , проте інтервал збіжності з нерівності
, проте інтервал збіжності з нерівності  Теорема не дає відповіді про збіжність на кінцях інтервалу, тому їх слід перевіряти окремо за відомими ознаками збіжності.
Теорема не дає відповіді про збіжність на кінцях інтервалу, тому їх слід перевіряти окремо за відомими ознаками збіжності.




