
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття і властивості визначника n-го порядкуСодержание книги
Поиск на нашем сайте
На практичних заняттях було введено поняття визначника другого і третього порядків. Це були числа, отримані за певними законами з таких таблиць- матриць другого і третього порядків відповідно: s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> Визначник другого порядка – це число, що позначається
Ми хочемо узагальнити це поняття, тобто отримати визначник Аналіз обчислення визначників другого і третього порядків приводить до доцільності такого означення: Означення. Визначником
називається алгебраїчна сума Отже визначник Для визначника вводять позначення:
Властивість 1. Визначник не зміниться, якщо його рядки зробити відповідними стовпцями. Розглянемо визначник d.
Стверджується, що Розглянемо загальний член визначника d: Це перетворення, при якому всі рядки стають відповідними стовбцями, називається транспонуванням. Властивість 2. Якщо в визначнику поміняти місцями будь які 2 рядки, то знак визначника зміниться на протилежний. Доведення за схемою властивості 1. Насправді, нехай у визначнику
Якщо Члену (1) у визначнику а у визначнику Підстановку (2) можна одержати з підстановки (1) однією транспозицією в верхньому рядку, тобто вона має протилежну парність. Звідси випливає, що всі члени визначника d входять до визначника d1 і відрізняються лише знаком. Властивість 3. Якщо в визначнику є нульовий рядок, то визначник дорівнює 0. Нехай усі елементи і-го рядка визначника є нулями За означенням визначник n-го порядку це алгебраїчна сума n доданків, кожний з яких є добутком n елементів, узятих по одному з кожного рядка й кожного стовпця матриці і т.д. Отже, у кожний член визначника повинен увійти множником один елемент з і-ого рядка, тому в нашому випадку всі члени визначника дорівнюють нулю. Що й треба було довести. Властивість 4. Якщо в визначнику є 2 рівних рядка, то визначник дорівнює 0. Доведення. Нехай у визначнику d рівні між собою і-рядок і j=рядок
Нехай d = k d1 – визначник d, в якому поміняли і з j рядок. Тоді за властивістю 2: d1=-k Але насправді нічого не змінилось, оскільки, i та j рядки рівні d1=d=k ⟹ -k=k Звідси, 2k=0, k=0. Властивість 5. Якщо всі елементи деякого рядка помножити на число r, то визначник зміниться в r разів. Доведення за схемою властивості 1. Цю ж властивість можна сформулювати у вигляді: якщо рядок визначника містить постійний множник, то його можна винести за знак визначника. Розглянемо визначник d:
Нехай на r помножені всі елементи і-ого рядка. Кожний член визначника містить рівно один елемент із і-ого рядка, тому всілякий член отримує множник r, тобто сам визначник множиться на r. Властивість 6. Якщо у визначнику є два пропорційні рядки, то визначник = 0. Доведення проводиться з використанням властивості 5 і властивості 4. Насправді, нехай елементи j-ого рядка визначника відмінюються від відповідних елементів і-ого рядка
Виносячи спільний множник r із j-ого рядка за знак визначника, ми отримуємо визначник з двома однаковими рядками, який дорівнює нулю за властивістю 4. Властивість 4 (а також властивість 3 при Властивість 7. Якщо кожний елемент і-рядка визначників є сумою 2-ох доданків, то такий визначник можна подати як суму двох визначників, у яких всі рядки, за винятком і-ого такі ж, як у початковому. і-й рядок першого визначника складається з перших доданків, і-ий рядок другого визначника складається з других доданків.
Доведення за схемою доведення властивості 1. Дійсно, всілякий член заданого визначника можна подати у вигляді:
Збираючи разом перші доданки цих сум (з тими ж знаками, які мали відповідні члени в заданому визначнику) ми отримаємо, очевидно, визначник n-го порядку, що відмінюється від заданого визначника лише тим, що в і-ому рядку замість елементів Властивість 8. Якщо до і-ого рядка визначника додати j-ий рядок, в подумках помножений на деяке число, то визначник не зміниться. Доведення. Нехай до і-го рядка визначника d додається j-ий рядок, помножений на k, тобто в новому визначнику всілякий елемент і-го рядка має вигляд Властивість 9. Якщо в визначнику присутній рядок, що є лінійною комбінацією інших рядків, то визначник дорівнює 0. Доведення. Нехай, наприклад, і-ий рядок буде лінійною комбінацією s інших рядків
Застосовуючи властивість 7, ми подамо наш визначник у вигляді суми визначників, у кожному з яких і-ий рядок буде пропорційним до одного з інших рядків. За властивістю 6 усі ці визначники дорівнюють нулю, дорівнює нулю, отже і заданий визначник теж. Ця властивість є узагальненням властивості 6, причому вона дає найзагальніший випадок рівності визначника нулю. Зауваження. Завдяки властивості 1 все, що було формульовано для рядків є правильним і для стовпців, тому властивість 1 називається властивістю рівноправності рядків і стовпців.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 721; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.76 (0.006 с.) |



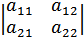 і яке дорівнює алгебраїчній сумі
і яке дорівнює алгебраїчній сумі  , аналогічно визначник третього порядку:
, аналогічно визначник третього порядку:
 -го порядку таким чином, що з нього при
-го порядку таким чином, що з нього при 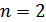 та
та  отримати попереднє.
отримати попереднє.
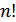 доданків, кожний з яких є добутком
доданків, кожний з яких є добутком  , де
, де 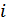 – кількість інверсій у перестановці α1,α2,…,αn.
– кількість інверсій у перестановці α1,α2,…,αn.


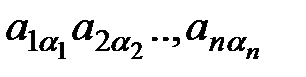 – загальний член d.
– загальний член d.
 (1)
(1)

 міняються місцями i-ий та j-ий рядки,
міняються місцями i-ий та j-ий рядки,  , а всі інші рядки залишаються на місці. Ми отримаємо визначник
, а всі інші рядки залишаються на місці. Ми отримаємо визначник  :
: .
. (1) є членом визначника
(1) є членом визначника  , то всі його елементи і у визначнику
, то всі його елементи і у визначнику 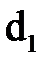 залишаються, очевидно, в різних рядках і різних стовпцях. Таким чином, визначники d та d1 складаються з одних і тих же членів.
залишаються, очевидно, в різних рядках і різних стовпцях. Таким чином, визначники d та d1 складаються з одних і тих же членів. (2),
(2), (3).
(3).


 одним і тим самим множником r.
одним і тим самим множником r.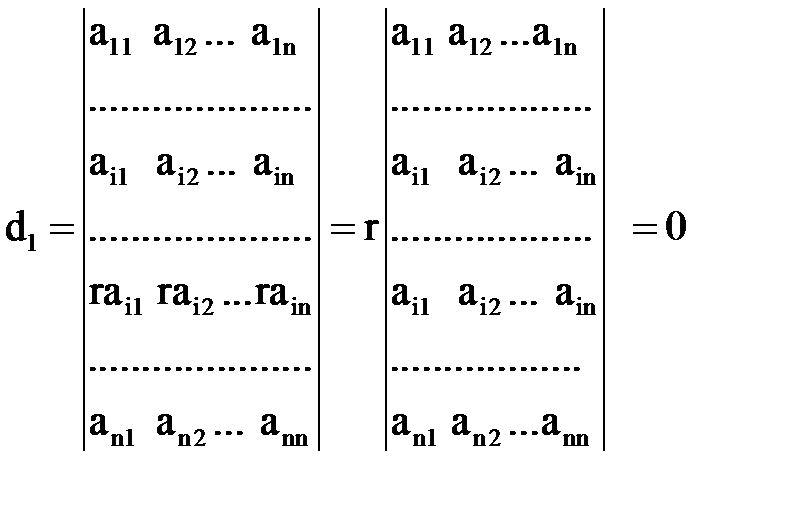
 ) є, очевидно, окремим випадком властивості 6 (при r = 1 і r = 0).
) є, очевидно, окремим випадком властивості 6 (при r = 1 і r = 0).



 стоять елементи
стоять елементи 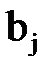 . Відповідно другі доданки складають визначник, в і-ому рядку якого стоять елементи
. Відповідно другі доданки складають визначник, в і-ому рядку якого стоять елементи  .
. . Тоді на підставі властивості 7 цей визначник дорівнює сумі двох визначників, з яких перший є d, а другий містить пропорційні рядки і тому дорівнює 0.
. Тоді на підставі властивості 7 цей визначник дорівнює сумі двох визначників, з яких перший є d, а другий містить пропорційні рядки і тому дорівнює 0.



