
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Побудова множини комплексних чисел.Содержание книги
Поиск на нашем сайте
Відомо,що існує взаємнооднозначна відповідність між точкою прямої і дійсними числами. Але маючи дійсні числа, неможна розв¢язати навіть таке просте рівняння Тоді спробували побудувати таку множину чисел, які б геометрично зображувалися не тільки точками прямої, а точками всієї площини.
y
b a
d b
x 0 a c Така спроба виявилась успішною. Побудована множина чисел була названа множиною комплексних чисел. Побудуємо спочатку множину комплексних чисел геометрично. Розглянемо площину, на якій введено декартову прямокутну систему координат. Числа, які ми хочемо побудувати, будемо зображувати точками цієї площини і позначати буквами грецького алфавіту. Кожна точка є упорядкованою системою координат (a,b), тобто двох дійсних чисел a =(a,b). Введемо для чисел- точок дві основні операції: додавання та множення a = (a, b), b = (c, d). Ознчення 1. Під сумою чисел-точок a і b розуміють таку точку, яку умовно позначаємо a +b = (a+c, b+d). Означення 2. Під добутком чисел-точок a і b розуміють таку точку, що умовно позначається a × b = (a×c-b×d, a×d+b×c).
Можна довести (пропонується зробити це самостійно), що введені операції мають такі властивості: 1. a + b = b + a (закон коммутативності додавання) 2. a + (b + g) = (a+b) + g (закон ассоціативності додавання) 3. a × b = b × a (закон комутативності множення) 4. (a × b) × g = a × (b × g) (закон ассоціативності множення) 5. a (b + g) = a × b + a × g (закон дистрибутивності) При цьому ми виходимо з такого означення рівності. Означення 3. Точки-числа вважаються рівними, якщо в них рівні відповідні декартові координати. З¢ясуємо питання про існування обернених операцій до операцій додавання та множення. Але спочатку дамо загальне означення операцій, обернених до даних. Нехай в множині М визначена бінарна внутрішня алгебраїчна операція (*). Означення 4. Говоритимемо, що в множині М існує обернена операція до операції (*), якщо для будь-якої упорядкованої пари (x,y) елемента з множини М існують єдині єлементи z1 та z2, що задовольняють рівності y * z1 = x, z2 * y = x, z1, z2 Î M. Зауважено, що коли операція (*) комутативна та елементи z1та z2 рівні. Застосуємо поняття оберненої операції для з¢ясування існування оберненої операції до додавання. Розглянемо будь-яку упорядковану пару чисел a, b. Поставимо питання: чи існує точка-число g(x, y), така що (c, d) + (x, y) = (a,b). За означенням 1 і 3 маємо: (c + x, d +y) = (a,b) c + x = a x = a - c d + y = b y = b - d Таким чином доведено, що така точка g = (a-c,b-d) існує. Отже додавання існує обернена операція, яка називається віднімання. Для точки g вводиться позначка g = a - b. З¢ясуємо питання для існування оберненої операції для множення, тобто чи існує для будь-якої пари-точок a, b така точка g = (x,y), що b × g = a. Використовуючи означення 2 та 3 маємо: b × g = (c×x - d×y, c×y + d×x) = (a, b)
Обчислимо визначник D системи: D = З теореми Крамера випливає, що ця система має єдиний розв¢язок.
Таким чином, ми довели, що обернена операція існує g = і називається діленням, крім ділення на β=(0,0). Введемо геометричне означення комплесних чисел. Означення 5. Множиною комплексних чисел називається множина чисел, що геометрично зображаються точками площини, для яких введено дві основні алгебраїчні операціїв відповідності з означенням 1 та 2 і рівність в відповідності з означенням 3. Оскільки точка ототожнюється з парою дійсних чисел (її координат), то означення 5 може бути формалізоване. Означення 5¢. Множиною комплексних чисел називають множину вселяких упорядкованих пар дійсних чисел, для яких введено дві алгебраїчні операції: додавання і множення згідно з означенням 1 і 2, та поняття рівності згідно означення 3.
Доведемо, що побудована система чисел є розширенням множини дійсних чисел, тобто: 1) всі дійсні числа належать побудованій множині чисел; 2) в побудованій множині є число, що не є дійсним, а саме - корінь рівняння Доведення. 1) Розглянемо точку-число виду (а,0) і ототожнемо таку точку-число з дійсним числом (с,0). Доведемо, що додавання в сенсі означення1, не суперечить звичайному додаванню дійсних чисел. Отже, задамо два числа вигляду (а,0) = а, (с,0) = с. Тоді за означенням 1 маємо (а,0) + (с,0) = (а+с,0). Отже отримали дійсне число а+с. Так само доведемо, що й друга операція не знаходиться в суперечності з означенням 2. За означенням 2 маємо: (а,0) × (с,0) = (а×с - 0×0, а×0 + 0×с) = (а×с,0). Тобто всі дійсні числа знаходяться на осі Ох, яку називають дійсною вісссю. 2) Розглянемо упорядковану пару дійсних чисел х = (0,1). Доведемо, що це комплексне число є коренем рівняння x2+1=0. Насправді:
Таким чином ми довели, що в множині крім дійсних чисел, міститься число, що точно не є дійсним (оскільки для жодного дійсного числа неможливе x2=-1). Для цього важливого числа вводять позначку (0,1) = і. Алгебраїчна форма комплексних чисел. Нехай задано комплексне число a = (a,b). Доведемо, що будь-яке комплексне число a можна подати у вигляді a = а + b×і. З означення додавання маємо a = (a,b) = (а,0) + (0,b). З означення множення випливає: (b,0) × (0,1) = (b×0 - 0×1, b×1 + 0×0) = (0,b). Таким чином ми довели, що число (0,b) = b×і. Отже, a = а + b×і. ця форма запису комплексного числа називається алгебраїчною. В алгебраїчному записі a = а + b×і, а – називається дійсною частиною комплексного числа, b – уявною частиною і позначаються вони a = Re a, b = Im a відповідно. Операції над комплексними числами в алгебраїчній формі. Нехай два комплексних числа в алгебраїчній формі a = (a,b) = a +bі, b = (c,d) = c +dі. Скористаємося правилом додавання за означенням 1 та поданням комплексного числа в алгебраїчній формі a + b = (a+c, b+d) = a+c + (b + d)і. Таким чином, ми отримали правила додавання в алгераїчній формі. Розглянемо тепер множення в алгебраїчній формі. За означенням 2 маємо a × b = (а×с-b×d, a×d+b×c) = (a×c-b×d) + (a×d+b×c)×і. Спробуємо перемножити a × b = (а+bі)×(c+d×і) = a×c+adі+bcі+bi2d, a × b = (а×с-b×d) + (b×c+a×d)і, тобто в алгебраїчній формі два комплексних числа перемножаються як дві суми, при цьому враховується, що i2=-1. Полярна система координат. Означення. Полярною системою координат називають систему координат на площині, що складається з числової прямої, яка називається полярною віссю і точки на ній, що називається полюсом.
Якщо ввести полярну систему координат, то положення точки М на площині визначається довжиною її радіуса-вектора Як завжди, додатній кут отримується поворотом проти годиникової стрілки. Якщо задані r та j, то точка визначається однозначно на пллощині. Якщо ж задати точку, то r визначається однозначно, а j - неоднозначно, а з точністю до доданка 2kπ. Для того, щоб ліквідувати таку неоднозначність, домовимось, розглядати кут в межах 0 £ p £ 2 або -p £ j £ p. Тоді виникає взаємнооднозначна відповідність між точками площини і числами r та j. Означення. Числа r та j називаються полярними координатами точки. Число r – полярним радіусом, кут j - полярним кутом точки М. Знайдемо зв¢язок між полярними координатами точки і декартовими прямокутними. Введемо декартову прямокутну систему координат таким чином, що її початок збігається з полюсом, а вісь Ох з полярною вісью. Використовуючи теорему про геометричний зміст декартових прямокутних координат, маємо
Якщо відомі r та j, то x і y можна обчислити за формулами x = r cos j y = r sin j. Поставимо обернену задачу: відомі x та y, треба знайти r та j. З попередніх рівностей маємо:
З цих рівностей випливає
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 579; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.130.96 (0.005 с.) |

 .
.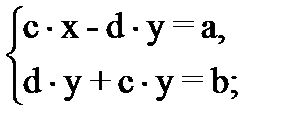
 , якщо виконується принаймні одна з нерівностей c≠0, d≠0.
, якщо виконується принаймні одна з нерівностей c≠0, d≠0.
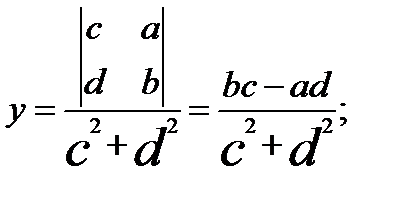

 ,
,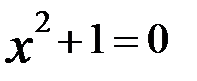 .
.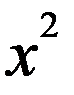 = (0,1)×(0,1) = (0×0 - 1×1, 0×1+1×0) = (-1, 0) = -1.
= (0,1)×(0,1) = (0×0 - 1×1, 0×1+1×0) = (-1, 0) = -1. і кутом між полярною віссю і радіусом-вектором
і кутом між полярною віссю і радіусом-вектором  .
.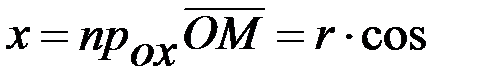 j.
j. 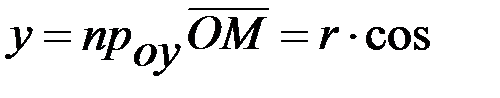 (90°-j) = r× sinj.
(90°-j) = r× sinj.
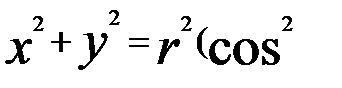 j+
j+ 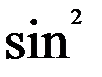 j),
j),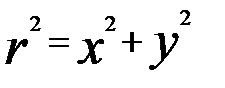 ,
, 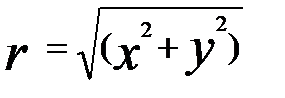 ,
,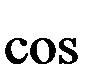 j
j 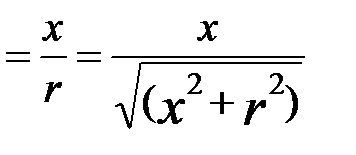 ,
,  j
j 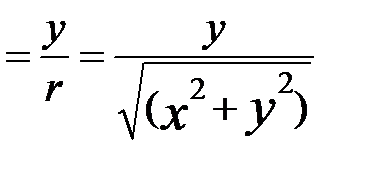 .
.


