
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття лінійно залежних і лінійно незалежних систем векторів.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Означення. Лінійною комбінацією векторів Означення 1. Система векторів Інакше кажучи, Означення 2. Система векторів
Теорема. При Доведення. Нехай система векторів лінійно залежна за означенням 1.Треба довести, що вона лінійно залежна у сенсі означення 2. Скористаємось означенням 1. Тоді виконується (1):
Додамо до обох частин даної рівності вектор протилежний до
Внаслідок комутативності і означення нульового вектора маємо:
Тобто
Нехай тепер система векторів лінійно залежна за означенням 2:
Треба довести, що Додамо вектор
Відомо, що
Тобто система є лінійно залежною за означенням 1. Теорему доведено. Зауваження. При Теорема. Якщо у системі векторів є лінійно залежна підсистема, то і вся система лінійно залежна. Доведення. Нехай задана система Запишемо рівність в такому виді:
Тоді Система лінійно залежна за означенням 2. Теорему доведено. Означення. Система векторів З вище доведеної теореми випливає, що якщо система лінійно незалежна, то всі її підсистеми також лінійно незалежні. Геометрична інтерпретація поняття лінійної залежності. З’ясуємо геометричний зміст поняття лінійної залежності. Теорема 1. Для того, щоб система з одного вектора була лінійно залежною, необхідно і достатньо, щоб цей вектор був нульовим. Теорему 1 було обґрунтовано у зауваженні попереднього параграфу. Теорема 2. Необхідною і достатньою умовою лінійної залежності двох векторів є їх колінеарність. Доведення. Необхідність. Припустимо, що вектори Доведемо, що вектори колінеарні. Отже один з векторів є лінійною комбінацією. Нехай це Достатність. Припустимо, що Можливі випадки: 1) Принаймні один з векторів нульовий. Тоді твердження очевидне, тому що в системі міститься лінійно залежна підсистема. 2) Обидва вектори ненульові. Для доведення потрібна така лема. Лема. Якщо Дійсно, якщо Згідно із лемою маємо, що Теорему доведено. Теорема 3. Необхідною і достатньою умовою лінійної залежності трьох векторів є їх компланарність. Доведення. Необхідність. Припустимо, що вектори Якщо серед векторів системи пара колінеарних, то очевидно, що вони є компланарними. Нехай тоді вектори попарно неколінеарні. Тоді за означенням 1 лінійної залежності існує вектор (наприклад, Візьмемо точку А і прикладемо до неї вектори
(для визначеності
Тоді з попередньої рівності випливає, що Достатність. Припустимо, що Якщо серед векторів системи пара колінеарних, то в системі є лінійно залежна підсистема і тому вся система залежна. Нехай тоді вектори попарно неколінеарні. Прикладемо вектори Оскільки Теорему доведено. Теорема 4. Довільні чотири вектори геометричного простору лінійно залежні. Доведення. Нехай маємо систему Візьмемо точку А і прикладемо до неї дані вектори. Побудуємо паралеліпіпед, діагональ якого є
За означенням додавання векторів маємо Тоді Теорему доведено. Зауваження. Мимохідь ми довели таке важливе твердження: будь-який вектор у просторі можна розкласти за трійкою некомпланарних векторів.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 776; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 називається вектор
називається вектор  де pi - будь-які числа.
де pi - будь-які числа. називається лінійно залежною, якщо принаймні один з векторів цієї системи є лінійною комбінацією інших.
називається лінійно залежною, якщо принаймні один з векторів цієї системи є лінійною комбінацією інших. .
. називається лінійно залежною, якщо існують числа
називається лінійно залежною, якщо існують числа  , серед яких принаймні одне
, серед яких принаймні одне  , що виконується рівність:
, що виконується рівність:
 .
. перше і друге означення лінійно залежної системи еквівалентні.
перше і друге означення лінійно залежної системи еквівалентні. .
. :
:

 , що виконується і рівність
, що виконується і рівність  (
( .
. до лівої та правої частини даної рівності:
до лівої та правої частини даної рівності:
 маємо:
маємо:
 , означення 1 лінійної залежності втрачає сенс, тоді як за означенням 2 рівність
, означення 1 лінійної залежності втрачає сенс, тоді як за означенням 2 рівність  , тобто
, тобто 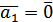 . Маємо, що система з одного вектора лінійно залежна тоді і тільки тоді, коли цей вектор нульовий.
. Маємо, що система з одного вектора лінійно залежна тоді і тільки тоді, коли цей вектор нульовий. – лінійно залежна. Тоді
– лінійно залежна. Тоді  :
:  .
.
 такі, що
такі, що  .
. .
. утворюють лінійно залежну систему.
утворюють лінійно залежну систему. (для визначеності). Тоді
(для визначеності). Тоді  , тобто вектори колінеарні.
, тобто вектори колінеарні. . Покажемо, що система лінійно залежна.
. Покажемо, що система лінійно залежна. , то
, то  :
:  , то
, то 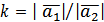 , якщо
, якщо  , то
, то  .
. утворюють лінійно залежну систему. Покажемо, що вони компланарні.
утворюють лінійно залежну систему. Покажемо, що вони компланарні. ), що є лінійною комбінацією інших
), що є лінійною комбінацією інших  .
. .
.


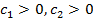 )
) – сторони і діагональ паралелограма. Отже ці вектори компланарні. Оскільки
– сторони і діагональ паралелограма. Отже ці вектори компланарні. Оскільки  , то вектори
, то вектори  також компланарні.
також компланарні. . Тоді
. Тоді  .
. , то
, то  . Тоді
. Тоді  , тобто
, тобто  . Якщо серед них є трійка компланарних, то вони очевидно лінійно залежні. Нехай такої трійки немає.
. Якщо серед них є трійка компланарних, то вони очевидно лінійно залежні. Нехай такої трійки немає.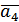 , а ребра знаходяться на прямих, що містять вектори
, а ребра знаходяться на прямих, що містять вектори 
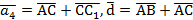 . Оскільки
. Оскільки  , маємо
, маємо  .
. , а тому
, а тому 


