
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тригонометрична форма комплексного числа. Операції множення та ділення в тригонометричній формі.Содержание книги
Поиск на нашем сайте
Нехай задано комплексне число a = (a, b) = a + b×і, де a і b – декартові прямокутні координати точки a, що зображає комплексне число. Введемо полярну систему координат таким чином, щоб полюс її збігався з початком декартової системи, а полярна вісь – з вісью 0х. Нехай точка a має полярні координати a (r,j). Використовуючи зв¢язок між декартовою і полярною системами, маємо a = a + bi = r×cosj + r×sinj Звідси a = r (cosj + isinj), отримана форма запису комплесного числа називається тригонометричною формою, r – модуль комплексного числа a (r = ½a½), j - аргумент к a (j = arg a). Таким чином ми довели, що будь-яке комплексне число можна записати в тригонометричній формі.
Розглянемо операції множення та ділення в тригонометричній формі. Нехай задно два комплексних числа в тригонометрчній формі a = r1 (cos b = r2 (cos Треба одержати a× b = r (cos j + i sin j). Для того, щоб це зробити перейдемо від тригонометричної фори до агебраїчної і перемножимо. a× b = ( = тобто a×b = Звідси випливає: r=r1r2, r=|a× b|, r1=|a|, r2=|b|, |a× b|=|a|×|b|. j = Таким чином ми одержали, що 1) модуль добутку двох комплексних чисел дорівнює добутку модулів. 2) аргумент добутку двох чисел дорівнює сумі аргументів. Підсумовуючи це, маємо Правило: Для того, щоб перемножити два числа в тригонометричній формі, треба перемножити їх модулі і додати аргументи. Розглянемо частку двох комплексних чисел в тригонометричній формі
Домножимо чисельник і знаменник на
Отже, отримали правило
Операції піднесення до степеня Поняття цілого степеня комплексного числа Домовились вважати 1) 2) Для корректності введеного поняття треба виконати вправу: 1) Довести
2) Довести 1. Розглянемо спочатку операцію піднесення в алгебраїчній формі. Нехай задано число
Розглянемо таблицю множення числа і
Використовуючи таблицю множення та виділяючи дійсну та уявну частину, отримаємо
2. Розглянемо операцію піднесення до степеню, коли
Використовуючи правило множення комплексних чисел в тригонометричній формі, маємо
Застосуємо отримані рівності (1) і (2) для знаходження розкладання Застосуємо до числа
Застосуємо формулу (1) при
Порівнюючи в формулах (3) і (4) дійсні та уявні частини, отримаємо
Операція здобуття кореня n-ого степеня з комплексного числа Нехай задане комплексне число Означення Коренем n-ого (n≥2) степеня з комплексного числа
Нехай число
Тобто, Порівнюючи дійсні та уявні частини, отримаємо дійсну нелінійну систему рівнянь.
Більш складна система виникає, якщо таким шляхом вилучати корені степеня n≥3. Розглянемо це питання для комплексного числа Шукатимемо За означенням, користуючись формулою Муавра, маємо
З цієї рівності випливає
Звідси випливає Отже
Насправді, щоб отримати всі корені достатньо змінювати
Тоді
Скористаємося періодичністю тригонометричних функцій, тоді
Отже, отримали формули
Зауваження В шкільному курсі символ
|
||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 689; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.84.179 (0.008 с.) |

 + i sin
+ i sin  )
) + i sin
+ i sin  ).
). cos
cos 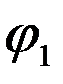 +
+ 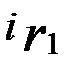 sin
sin  ) (
) ( ) =
) = ,
,
 (cos(
(cos( +
+  )+i×sin(
)+i×sin( +
+  )).
)).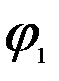 +
+  , j = arg (ab),
, j = arg (ab),  = arg a,
= arg a,  = arg b, arg (ab) = arg a + arg b.
= arg b, arg (ab) = arg a + arg b.



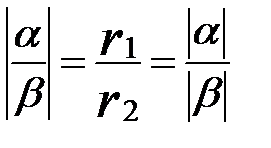 , arg (
, arg (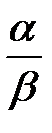 ) =
) =  ×
× 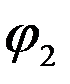 = arg a - arg b.
= arg a - arg b. вводиться так само як і для дійсного числа. Нагадаємо, що
вводиться так само як і для дійсного числа. Нагадаємо, що  при
при  .
. . Для введення
. Для введення 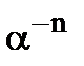 існують два шляхи.
існують два шляхи. , де
, де 


 при
при  .
. . Оскільки з попередніх означень випливає, що піднесення до цілого степеня зводиться до піднесення до натурального степеня, то можна скористатися формулою Бінома Ньютона:
. Оскільки з попередніх означень випливає, що піднесення до цілого степеня зводиться до піднесення до натурального степеня, то можна скористатися формулою Бінома Ньютона:
 з цього випливає
з цього випливає 

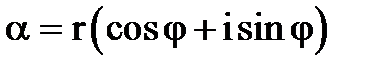
 .
. - формула Муавра
- формула Муавра
 і
і  через
через  і
і  . Окремі випадки цих формул при n=2,3 відомі зі шкільного курсу.
. Окремі випадки цих формул при n=2,3 відомі зі шкільного курсу. формулу (2). В тригонометричній формі
формулу (2). В тригонометричній формі 
 (3)
(3) , отримаємо
, отримаємо
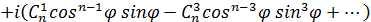

 (4)
(4) таке, що
таке, що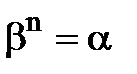 .
.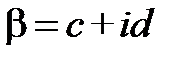 . Розглянемо найпростіший випадок n=1. Тоді за попереднім означенням треба знайти дійсні числа с і d такі що
. Розглянемо найпростіший випадок n=1. Тоді за попереднім означенням треба знайти дійсні числа с і d такі що


 .
. .
.
 (арифметичний корінь),
(арифметичний корінь), 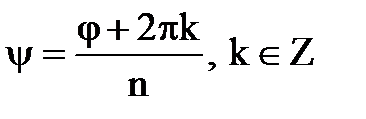 .
.
 . Нехай
. Нехай  . Доведемо, що
. Доведемо, що  збігатиметься з одним з коренів
збігатиметься з одним з коренів 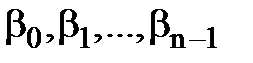 . Поділимо к на n:
. Поділимо к на n: .
.


 вживався лише для арифметичних коренів. Тепер ми вживатимемо цей символ в більш широкому сенсі.
вживався лише для арифметичних коренів. Тепер ми вживатимемо цей символ в більш широкому сенсі.


