
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття базису простору і площиниСодержание книги
Поиск на нашем сайте
Означення. Максимальною лінійно незалежною системою векторів простору (площини) називається така лінійно незалежна система векторів, приєднання до якої будь-якого вектору простору (площини) приводить до лінійно залежної системи. Означення. Базисом називається упорядкована максимальна лінійно незалежна система векторів простору(площини). З попереднього випливає, що базисом площини є будь-яка упорядкована система двох неколінеарних векторів, а базисом простору – будь-яка упорядкована трійка некомпланарних векторів. Теорема. Будь-який вектор площини(простору) можна розкласти і при тому єдиним чином за векторами базису. Доведення. Доведемо цю теорему в просторі. Розглянемо базисні вектори Зауважимо, що можливість розкладання доведено у теоремі 4 про геометричний зміст лінійної залежності. Тож маємо Доведемо єдиність розкладання. Припустимо супротивне, що для
Зауважимо, що оскільки розкладання відрізняються, то різними є принаймні одна пара коефіцієнтів ci, di. Припустимо (для визначеності), що Тоді отримуємо:
Оскільки Теорему доведено. Означення. Координатами вектора у заданому базисі називаються коефіцієнти розкладання цього вектора за векторами базису. Афінна система координат. Розглянемо площину або простір. Означення. Афінною системою координат називається система, що складається з точки, яку називають початком системи координат, і базису Означення. Радіус-вектором точки називається вектор, початком якого є початок системи координат, а кінцем - дана точка. Означення. Афінними координатами точки називаються координати її радіус-вектора у даній афінній системі координат. Твердження. Нехай задано вектор Доведення. У афінній системі координат задані координати точки А, отже:
Отримали, що Теорему доведено. Прямокутна декартова система координат є окремим випадком афінної системи координат. При цьому базисні вектори взаємно перпендикулярні і мають одиничну довжину. Вони позначаються:
Додатковий матеріал з векторної алгебри Для оволодіння рештою інформації з векторної алгебри пропонується написання реферату за наступною схемою. Схема написання теоретичної частини I. Скалярний добуток 1. Скалярна проекція вектора на вісь. Почнемо з допоміжного поняття величини напрямленого відрізку. Розглянемо вісь u і напрямлені відрізки на осі u. Означення 1. Величиною напрямленого відрізку
Розглянемо тепер вектори, що не обов’язково належать осі u.
Означення 2. Векторною проекцією вектора AB на вісь u називається вектор Позначимо векторну проекцію
Означення 3. Скалярною проекцією
Теорема 1. Скалярна проекція вектора на вісь дорівнює добутку довжини цього вектора на косинус кута між вектором та віссю. Доведення. (навести доведення) Для доведення властивостей скалярних проекцій векторів корисною є теорема про геометричний зміст декартових прямокутних координат. Теорема 2. Декартові прямокутні координати є проекціями вектора на відповідні координатні осі. Скалярна проекція має такі властивості. Теорема 3. Скалярна проекція суми двох векторів дорівнює сумі скалярних проекцій цих векторів
Доведення. (навести доведення) Теорема 4. Скалярна проекція добутку вектора на число дорівнює добутку цього числа на скалярну проекцію вектора
2. Поняття скалярного добутку. Означення 3. Скалярним добутком двох векторів
Останню рівність можна записати у вигляді
або
Звідси випливає інше означення скалярного добутку. Означення 4. Скалярним добутком векторів 3. Алгебраїчні та геометричні властивості скалярного добутку Доведемо, що скалярний добуток має такі алгебраїчні властивості: 1) 2) 3) 4) (навести доведення перелічених властивостей). Зауваження. З властивостей 3) та 1) випливає, що Зі скалярним добутком пов’язана така геометрична властивість: Для того щоб вектори були ортогональними (перпендикулярними) необхідно і достатньо, щоб їх скалярний добуток дорівнював нулю (навести доведення необхідності і достатності умови).
4. Вираз скалярного добутку через координати векторів Означення. Базис простору (площини) називається ортонормованим, якщо він складається з попарно ортогональних векторів, довжина яких дорівнює одиниці. Нехай в просторі введено ортонормований базис
Теорема. Скалярний добуток
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1716; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

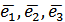 . Візьмемо довільний вектор
. Візьмемо довільний вектор  .
. .
. .
. .
.

 , що стверджує про лінійну залежність векторів базису. Отримано суперечність до означення базису.
, що стверджує про лінійну залежність векторів базису. Отримано суперечність до означення базису. (для площини),
(для площини),  (для простору).
(для простору). , причому точка А в деякій афінній системі координат має координати
, причому точка А в деякій афінній системі координат має координати  , а точка B у цій же системі –
, а точка B у цій же системі – 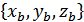 . Тоді координатами вектора
. Тоді координатами вектора  .
.


 має координати
має координати 
 називається число, що позначається
називається число, що позначається  :
:
 , де
, де  ортогональна проекція точки A,
ортогональна проекція точки A,  – отрогональна проекція точки B.
– отрогональна проекція точки B.
 вектора
вектора  .
. .
. .
. і
і  називається число
називається число  , що дорівнює добутку довжин цих векторів на косинус кута між ними.
, що дорівнює добутку довжин цих векторів на косинус кута між ними.



 (властивість симетрії)
(властивість симетрії) (дистрибутивність)
(дистрибутивність)

 .
.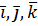 , тобто
, тобто 
 нехай далі вектори
нехай далі вектори  , відповідно.
, відповідно. в ортонормованому базисі дорівнює сумі добутків відповідних координат векторів
в ортонормованому базисі дорівнює сумі добутків відповідних координат векторів 



