
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування теорії визначників до лінійних систем алгебраїчних рівнянь. Теорема Крамера та лема до неїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Лема. Нехай задано визначник d n-го порядку. Сума добутків елементів і-го рядка на алгебраїчні доповнення до відповідних елементів j-го рядка дорівнює 0. Доведення. Нехай задано довільний визначник:
Доведемо, що Для доведення побудуємо допоміжний визначник, який буде відрізнятися від визначника d лише одним рядком.
Цей визначник за властивістю 4 дорівнює 0. Застосуємо до j-го рядка визначника наслідок з теореми Лапласа.
Залишилось довести, що Означення. Визначником системи називається визначник складений з коефіцієнтів при невідомих. Теорема Крамера. Нехай задано систему n алгебраїчних рівнянь з n невідомими, визначник якої не нульовий. Тоді невідома xk дорівнює дробу, знаменником якого є визначник системи, а чисельником також є визначник, який можна отримати з визначника системи заміною k-го стовпця стовпцем вільних членів. Доведення. Розглянемо систему
Помножимо обидві частини 1-го рівняння на А1k, 2-го на А2k, n-го на Аnk. Тоді отримаємо
Введемо в розгляд деякий визначник.
Застосуємо до k-го рядка цього визначника наслідок теореми Лапласа Застосуємо лему, тоді з рівності (3) маємо
Отже
Теорему Крамера доведено. Векторний простір Подальше вивчення векторного простору. У довільному векторному просторі означення лінійно залежних і лінійно незалежних систем векторів, а тому і максимально лінійно незалежних систем і базису, переносяться один до одного з геометричного простору. В цьому курсі розглядаються лінійні простори, базиси яких містять скінчену кількість векторів. Теорема. Будь-який вектор лінійного(векторного) простору єдиним чином розкладається за базисом. Доведення. Нехай задано довільний векторний простір V і його базис
1. Доведення можливості розкладання. Розглянемо систему Припустимо, що Це означає, що вектори базису лінійно залежні, що суперечить означенню. Отже З рівності випливає можливість доведення, адже:
2. Доведення єдиності розкладання. Припустимо, що існує вектор
Для визначеності нехай
Отже, ми отримали, що базисні вектори є лінійно залежними, що суперечить означенню базиса. Теорему доведено. Означення. Коефіцієнти розкладання вектора Вправа. Довести, що: Координати вектора суми двох векторів дорівнюють сумі відповідних координат. Координати добутку вектора на число можна отримати множенням його координат на це число. Означення. Лінійний простір називається n-вимірним, якщо в ньому існує n лінійно незалежних векторів, а будь-яка система з n+1 вектора лінійно залежна. З'ясуємо вимірність арифметичного простору. Доведемо таку теорему. Теорема. При
арифметичного простору лінійно залежна. Доведення. Розглянемо рівність (*) з означення лінійно залежної і лінійно незалежної системи:
З'ясуємо, при яких
З цієї векторної рівності отримаємо п-числових різностей.
Отримали систему n-рівнянь з s-невідомими. Ця система завжди сумісна тому що вона має принаймні один нульовий розв'язок. Але за допомогою елементарних перетворень вона зводиться до кінцевого вигляду, де кількість рівнянь менша за кількість невідомих. Повертаючись до рівності (*) приходимо до висновку що рівність (*) виконується коли принаймі одне з Наслідок. Будь-яка система з n + 1 вектора з п-компонентами є лінійно-залежна. Це негайно випливає, якщо з покласти З цього випливає, що вимірність арифметичного простору не більш ніж: п. Для того, щоб довести, що вимірність дорівнює n треба знайти принаймні одну лінійно незалежну систему векторів, що містить n-векторів. Такою системою векторів є наприклад:
Доведемо, що вони лінійно незалежні. Складемо рівність (*).
З цього випливає
Тобто (*) виконується лише один раз при Отже, ми довели, що арифметичний простір є n-вимірним (n – кількість компонент вектора). Зауваження. Поняття вимірності лінійного простору можна ввести і за таким означенням. Означення. Вимірністю лінійного простору називається кількість векторів, що входять до базису. Для того щоб це означення було корректним треба було б довести, що усі базиси даного простору містять однакову кількість векторів (насправді, це так). Позначимо n-вимірний довільний векторний простір через Vn. Введемо поняття підпростору даного простору Vn. Означення. Підмножина Безпосередньо з означення лінійного простору випливає, що для того щоб переконатися, що підмножина Доведемо це. Нехай в Якщо а) б) Зрозуміло, оскільки всі елементи множини Доведемо, що виконується умова – аксіома 3), 4), тобто що
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |





 . Ці рівності випливають з того, що при побудові алгебраїчних доповнень до елементів j-го рядка цей рядок викреслюється, а визначники d і d1 відрізняються лише j-тим рядком.
. Ці рівності випливають з того, що при побудові алгебраїчних доповнень до елементів j-го рядка цей рядок викреслюється, а визначники d і d1 відрізняються лише j-тим рядком. (1)
(1) (2)
(2)
 k=1,2,…,n (3)
k=1,2,…,n (3)
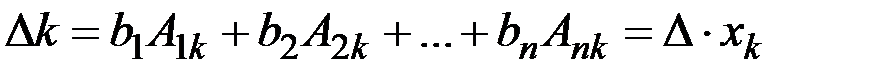



 . Розглянемо довільний вектор
. Розглянемо довільний вектор  , що належить V.
, що належить V. – лінійно залежну за означенням базису. Тоді існують числа
– лінійно залежну за означенням базису. Тоді існують числа  , серед яких
, серед яких 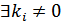 . Доведемо, що саме
. Доведемо, що саме  .
. . Тоді
. Тоді  .
. .
.
 (1)
(1) (2)
(2) . Помножимо рівність (2) на -1 і додамо до (1).
. Помножимо рівність (2) на -1 і додамо до (1).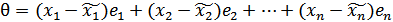
 система векторів
система векторів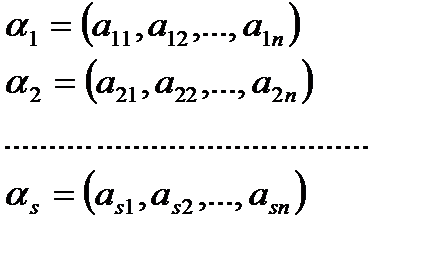

 вона виконується:
вона виконується:
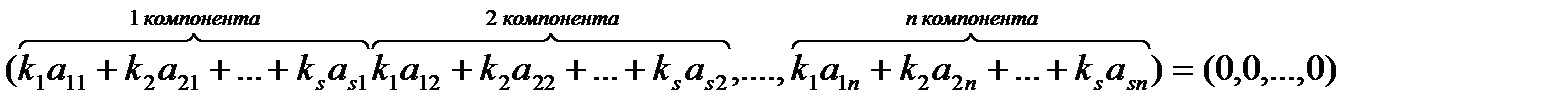

 -тих не дорівнює нулю, тому
-тих не дорівнює нулю, тому  -лінійно залежні.
-лінійно залежні. .
.
 (*)
(*)


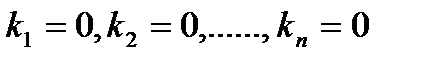
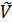 лінійного простору Vn називається підпростором даного простору, якщо
лінійного простору Vn називається підпростором даного простору, якщо  ,то
,то ;
; .
. . Наспправді, нехай
. Наспправді, нехай  , оскільки
, оскільки  , а при
, а при  .
.


