
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матриці обернені до даних. Умови їх існування.Содержание книги
Поиск на нашем сайте
Внаслідок того, що множення матриць, взагалі кажучі, не комутативне, в цьому питанні слід розглядати ліві обернені матриці праві. Означення. Матриця, що умовно позначається Означення. Матриця, що умовно позначається Для з’ясування умов існування обернених матриць введемо поняття невироджених (неособливих) і вироджених (особливих) матриць. Означення. Квадратна матриця називається невиродженою, якщо її визначник не дорівнює нулю. В противному разі квадратна матриця називається виродженою. Теорема 1. Жодна вироджена матриця не має ні лівої оберненої, ні правої оберненої матриці. Доведення. Нехай задана матриця А, det A = 0. Треба довести, що не існує ні правої оберненої, ні лівої оберненої матриці. Припустимо, що існує хоча б одна з них. Нехай існує ліва обернена матриця. Тоді det E = det 1 = 0, отримали суперечність. Таким чином, не існує Теорему доведено. Теорема 2. Для будь-якої невиродженої матриці існує і ліва обернена, і права обернена, і вони рівні. Доведення. Нехай задано матрицю А.
причому det A = d Треба довести, що існує ліва обернена, права обернена матриці, та
Доведемо, що 1) А 2) Доведемо 1) Застосувавши правило множення, лему до теореми Крамера і наслідок з теореми Лапласа маємо: А ×
Так само, безпосереднім множенням матриць доводиться друга рівність. З першого пункта випливає
Отже ми довели існування оберненої матриці та її обчислення:
Вправа. Довести єдиність матриці Операції додавання і множення на число. Означення. Сумою матриць А і В, А=( D = ( Означення. Добутком матриці А на число k, називається матриця F, елементи якої обчислюються за законом F = (k Введені операції мають такі властивості: 1) А + В = В + А; 2) (А + В)+С = А+(В + С); 3) $ Q: А + Q = А + Q + А; Q = 4) " А $ (-А): А + (-А) = (-А) + А = 0. Вона і снує, тому що є (-А) = (- 5) А = А; 6) k (l A) = (k l) A; 7) k (A + B) = kA + kB; 8) (k + l) A = kA + lA: Перевірити самостійно. Таким чином, множина всіх матриць є векторним простором, більш того, арифметичним, вимірності Розглянемо хоча б один базіс цього простору. Це так звані матриці
Таких матриць існує n2.
Доведемо, що це базис. Доведемо, що це лінійно незалежні матриці. Для цього з’ясуємо, при яких kij виконується рівність
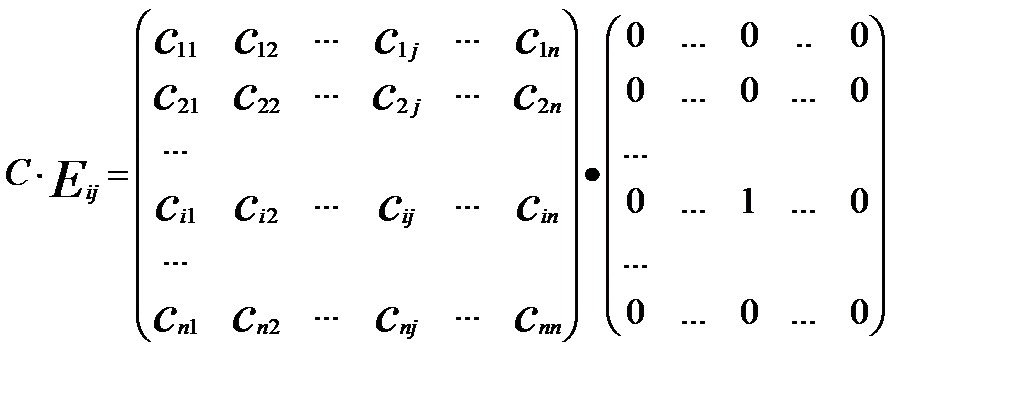
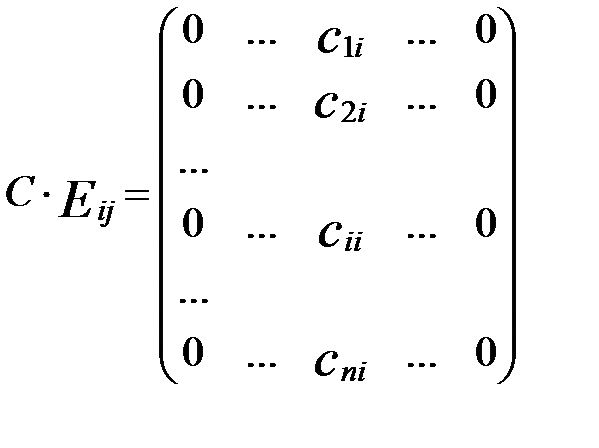
Отже рівність (*) виконується лише в нульовому випадку усіх kij, тому матриці лінійно залежні. З того, що вимерність простору матриць дорівнює Розглянемо довільну матрицю А. Доведемо, що А = Введемо в розгляд допоміжну матрицю:
Доведемо, що цю матрицю можна подати у вигляді Насправді
Розглянемо тепер матрицю А. Її можна подати у вигляді
Застосуємо до кожного доданку попередню формулу
Вправа. Довести, що операція множення матриць і додавання матриць підпорядковується дистрибутивному закону: А (В + С) = АВ + ВС.
Доведення. Необхідність. Нехай матриця С є скалярною. Треба довести, що С = Вище було доведено, що така матриця комутує з будь-якою матрицею А. Таким чином, необхідність доведена. Достатність. Нехай деяка матриця С загального вигляду С = комутує з будь-якою матрицею А. Треба довести, що матриця С – скалярна матриця, тобто З того, що
Матриці (1), (2) за умовою теореми рівні, тому що на однакових місцях повинні знаходитись рівні елементи. Порівняємо елементи i-тих рядків ицх матриць. 0 = Таким чином, ми одержали, що матриця С має діагональні елементи рівними, а елементи позадіагональні є нульовими, тобто матриця С – скалярна матриця.
Скалярні матриці. Означення. Скалярною матрицею називається матриця вигляду
До класу скалярних матриць належить одинична матриця, а також нульова. Позначимо k × Е = Доведемо, що кЕ комутує з будь-якою матрицею (к Е) А = А (к Е), Безпосереднім множенням матриць, переконуємося 1) (к Е) А = 2) А (к Е) =
Звідси випливає, що скалярна матриця комутує в добутку з будь-якою матрицею А. Насправді справедливе і обернене. А тому має місце така теорема. Теорема. Для того, щоб матриця була скалярною, необхідно і достатньо, щоб вона комутувала з будь-якою матрицею.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1026; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.198.201 (0.007 с.) |

 , називається лівою оберненою до матриці А, якщо вона задовольняє умову
, називається лівою оберненою до матриці А, якщо вона задовольняє умову 
 .
. , називається правою оберненою до матриці А, якщо вона задовольняє умову
, називається правою оберненою до матриці А, якщо вона задовольняє умову  .
.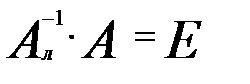 (з означення). Застосуємо теорему про визначник добутку матриць:
(з означення). Застосуємо теорему про визначник добутку матриць: . det A,
. det A,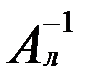 , так само доводиться, що не існує
, так само доводиться, що не існує  .
. ,
, 0.
0. =
=  . З матриці А побудуємо матрицю
. З матриці А побудуємо матрицю 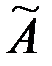 , заміною кожного елемента aij його алгебраїчним доповненням Аij і протранспонувавши отримаємо матрицю:
, заміною кожного елемента aij його алгебраїчним доповненням Аij і протранспонувавши отримаємо матрицю: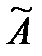 =
= 
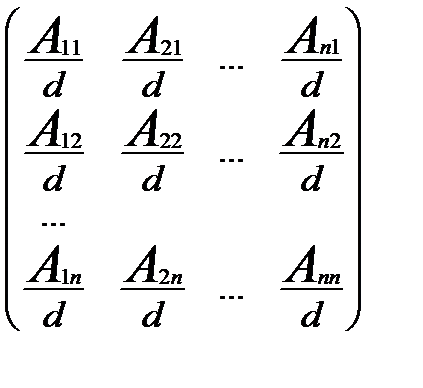 .
. = Е;
= Е;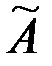 А = Е.
А = Е. =
= 
 =
=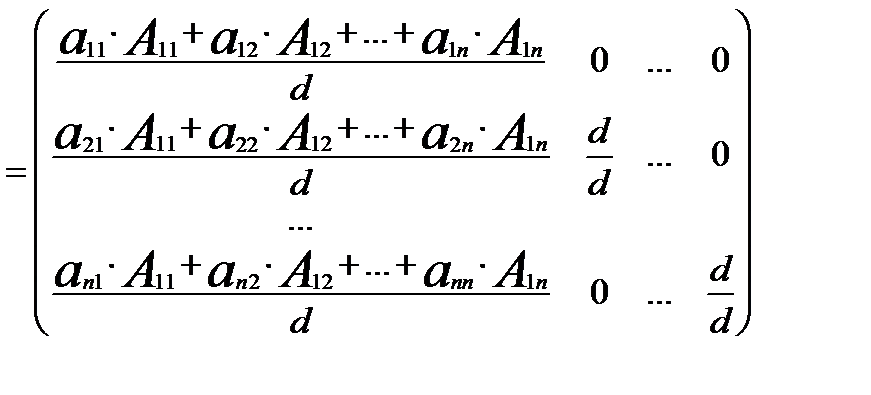 =
= 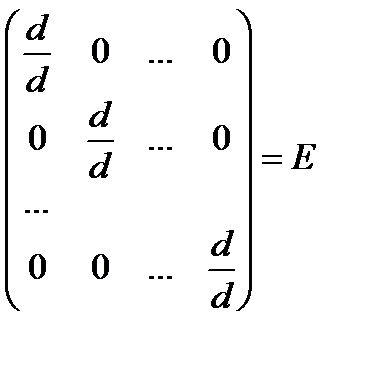 .
.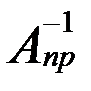 , а з другого пункту
, а з другого пункту  .
.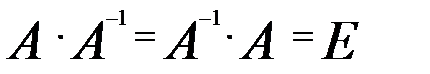 .
. =
=  .
. (Доведення проводиться за схемою доведення єдиності протилежного вектора).
(Доведення проводиться за схемою доведення єдиності протилежного вектора). ), В=(
), В=(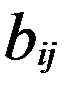 ), називається матриця D, елементи якої обчислюються за законом
), називається матриця D, елементи якої обчислюються за законом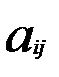 +
+  ).
).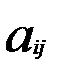 ).
). .
.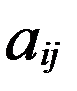 ).
). .
.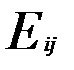 .
.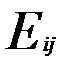 =
= 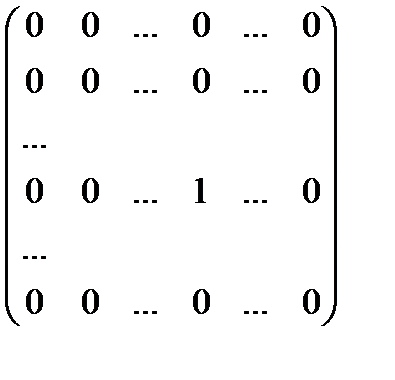 .
. ,
, 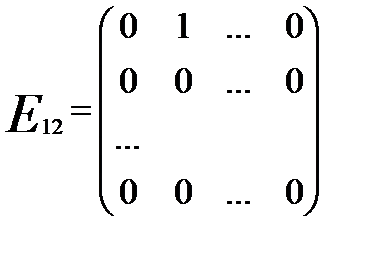 , …,
, …, 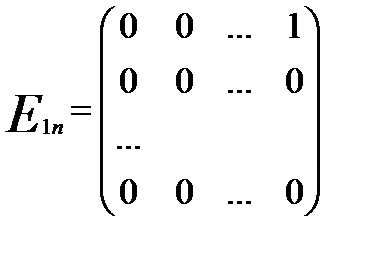 ,
, ,
,  , …,
, …, 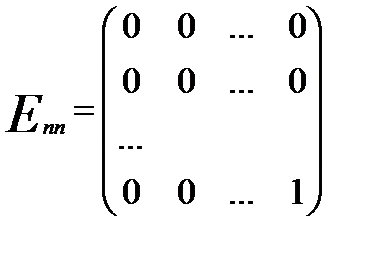
 (*)
(*)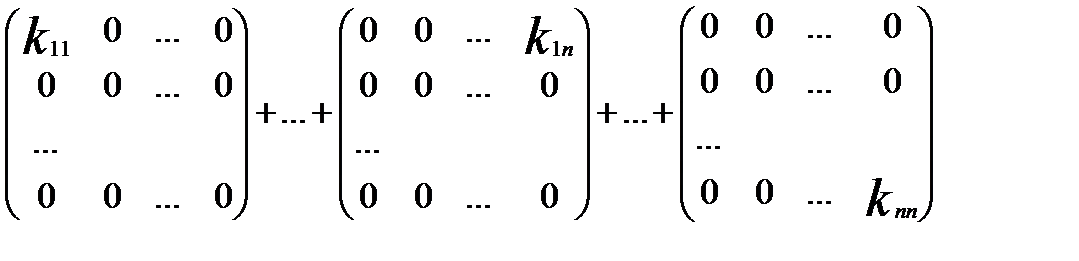 = 0.
= 0. ,
, 
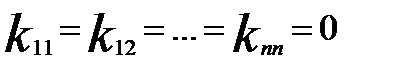 .
. , випливає, що матриці
, випливає, що матриці 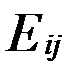 утворюють базіс. Тоді будь-яка матриця А повинна бути лінійною комбінацією матриць
утворюють базіс. Тоді будь-яка матриця А повинна бути лінійною комбінацією матриць  . Знайдемо цю лінійну комбнацію.
. Знайдемо цю лінійну комбнацію.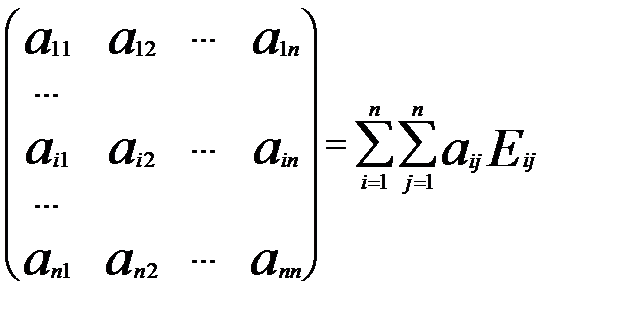 .
.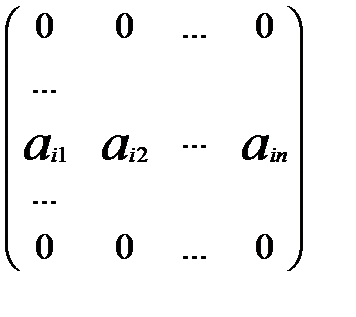 .
.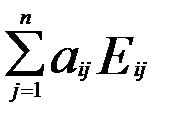 .
.
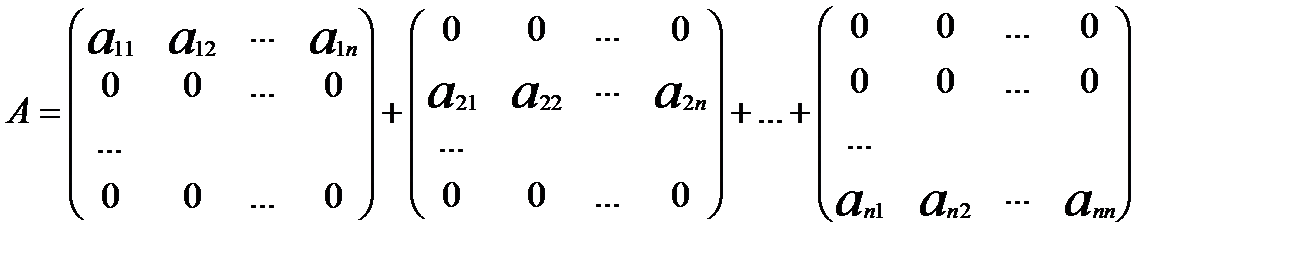
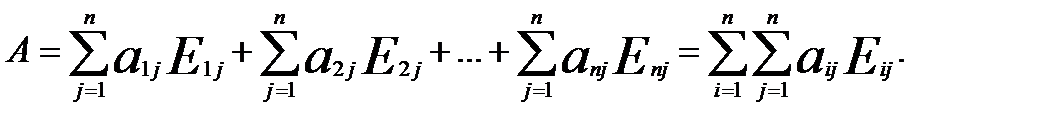
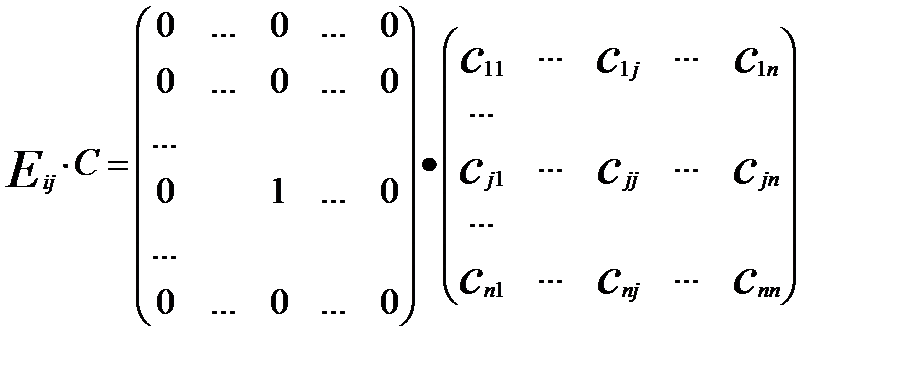
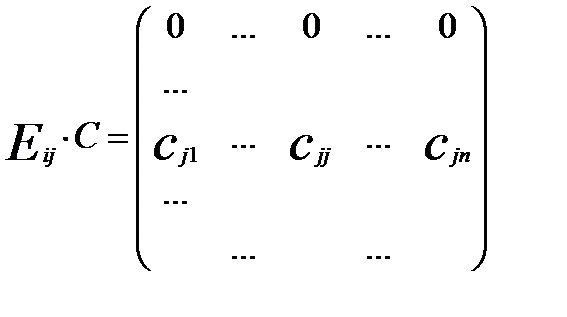
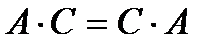 , " А. З того, що матриця С скалярна, вона має вигляд
, " А. З того, що матриця С скалярна, вона має вигляд
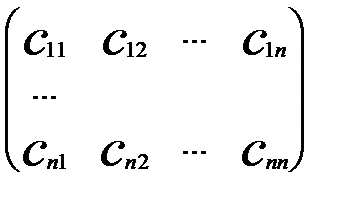 ,
, ,
,  , якщо i ¹ j.
, якщо i ¹ j.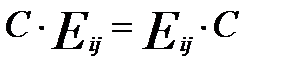 .
.
 (1)
(1) .
. (2)
(2) , 0 =
, 0 = 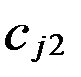 , …,
, …,  , 0 =
, 0 = 
 .
. .
. А.
А. .
. .
.


