
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття рангу системи векторів.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нехай задано систему векторів довільного простору:
Означення. Максимальною лінійно незалежною підсистемою даної системи векторів називається така її лінійно незалежна підсистема приєднання до якої будь-якого вектора цієї ж системи приводить до лінійно залежної системи. Означення. Рангом системи векторів (1) називається кількість векторів, що входить до максимальної лінійно-незалежної її підсистеми. Зауваження Для того, щоб означення вимірності лінійного простору і означення рангу системи векторів було коректним, треба було б довести, що кількість векторів, що входять в будь-яку максимальну лінійно незалежну систему простору (а для рангу – будь-яку максимально-лінійно незалежної підсистеми) є однаковим. Для подальшого потрібне таке означення. Означення 1. Говоритимемо, що система векторів (1)
Означення 2. Системи векторів (1) і (2) називаються еквівалентними, якщо кожна з них лінійно виражається через другу Властивість (транзитивності) Якщо система векторів (1) лінійно виражається через систему векторів (2), а система (2) через систему (3), тоді система (1) лінійно виражається через (3). Доведення. Для зручності доведення цієї властивості введемо символ Нехай задано суму однотипних доданків
Застосовуючи двічі цей символ, отримаєм для
Доведемо таку властивість: Для цього доведемо, що
Отже
Тепер перейдемо до доведення попередньої властивості транзитивності. Нехай задано системи:

За умовою (1) лінійно виражається через (2). Тоді за означенням
За умовою (2) лінійно виражається через (3), тому
Підставимо (5) в (4), тоді отримаємо
Отже доведено, що система векторів (1) лінійно виражається через систему (3). Наслідок. Якщо система векторів (1) еквівалентна системі (2), а система (2) еквівалентна системі (3), то системи (1) і (3) еквівалентні. Транзитивність еквівалентних систем доводиться повторенням двічі наведених міркувань.
Поняття рангу матриці. Теорема про ранг матриці. Розглянемо довільну матрицю.
Кожний стовпець матриці можна розглядати як упорядковану Використовуючи цю інтерпретацію і означення рангу системи векторів приходимо до доцільності такого означення. Означення. Рангом матриці називається кількість стовпців, що входить до максимальної лінійно незалежної підсистеми стовпців матриць. Або в скороченому вигляді можна дати таке формулювання. Означення. Рангом матриці називається максимальна кількість лінійно-незалежних стовпців. Теорема про ранг матриці. Найвищий порядок мінорів матриці, що не дорівнюють нулю, дорівнює рангу матриці. Доведення. Нехай найвищий порядок мінорів, що не дорівнюють нулю є число р. Це означає, що в матриці А є мінор р-того порядку, не рівний нулю. Мінори р + 1 і більш високих порядків дорівнюють нулю. Для визначеності припустимо, що мінор р-того порядку не рівний нулю знаходиться в лівому верхньому куту.

Треба довести, що ранг матриці Для цього треба довести два факти: 1) в матриці А є р-лінійно-незалежних стовпців; 2) всі інші стовпці через них лінійно виражаються. 1) Доведемо, що лінійно незалежними (за нашим припущенням) є перші р стовпців матриці. Припустимо супротивне, що перші р стовпців матриці лінійно залежні. Тоді з означення лінійної залежності випливає, що існують числа
Розглянемо цю рівність покомпонентно: І компонента - р компонента - ………………………………………………
З перших р рівностей випливає що стовпці мінора М - лінійно залежні. Доведемо, що тоді мінор М дорівнює нулю. Розглянемо два випадки. а) р = 1 тобто М = б) р≥2 В цьому випадку лінійна залежність означає, що в мінорі М існує стовпець, що є лінійною комбінацією інших стовпців, а тоді за властивістю визначників мінор М = 0 Отже, ми прийшли до суперечності умові. Отже, перші р стовпців матриці А- лінійно незалежні. Для доведення другого факту побудуємо визначник.

Доведемо, що при всіх таких і та к визначник Для доведення розглянемо два випадки: 1) 2) Розкладемо визначник за останнім рядком:
Розв'яжемо цю рівність відносно
Надамо всі значення
Це означає, що к- тий стовпець матриці А є лінійною комбінацією перших р-стовпців. Оскільки к набуває значень Що і треба було довести Таким чином за означенням ранг дорівнює р. Наслідки з теореми про ранг: Наслідок 1. Максимальна кількість лінійно-незалежних рядків матриці дорівнює максимальному числу лінійно-незалежних стовпців матриці, тобто дорівнює рангу матриці. Доведення: Розглянемо довільну матрицю А
Нехай максимальна кількість лінійно-незалежних стовпців = р, тобто Треба довести, що максимальна кількість лінійно-незалежних рядків = р. Для доведення побудуємо транспоновану матрицю
1) Доведемо, що ранг матриці А' дорівнює р.
З того, що Всі мінори матриці А в транспонованому вигляді знаходяться в матриці А'. Відомо, що при транспонуванні визначник не змінюється. Тому в матриці А' є мінор р - того порядку не рівний нулю, а всі мінори більш високих порядків дорівнюють нулю. З теореми про ранг випливає, що Тоді за означенням в матриці А' лише р лінійно незалежних стовпців, а вони є рядками матриці А Наслідок 2. Для того щоб визначник дорівнював нулю. Необхідно, щоб його рядки (стовпці) були лінійно залежними. Доведення: Нехай визначник
Розглянемо матрицю, що відповідає цьому визначнику
Доведемо, що Припустимо супротивне, що А за умовою Тоді за означенням рангу в матриці А лише р лінійно незалежних стовпців, інші n-р є їх лінійними комбінаціями. Тобто, загалом стовпці лінійно залежні. Тепер ми можемо сформулювати необхідну і достатню умову рівності визначника нулю. Теорема. Для того, щоб визначник п - того порядку дорівнював нулю необхідно і достатньо, щоб його рядки (стовпці) утворювали лінійно залежну систему. Доведення: Необхідність: є другим наслідком теореми про ранг. Достатність: Нехай рядки (стовпці) лінійно залежні, треба довести, що При доведенні виникають два випадки. 1) 2) А тоді за властивістю 9 визначників визначник дорівнює нулю.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 732; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.145.168 (0.006 с.) |

 (1)
(1) , якщо кожний вектор системи (1) є лінійною комбінацією векторів системи (2):
, якщо кожний вектор системи (1) є лінійною комбінацією векторів системи (2): (3)
(3) .
.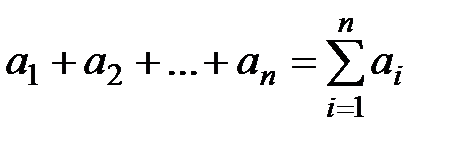



 . Для доведення проведемо підсумування за стовпцями
. Для доведення проведемо підсумування за стовпцями
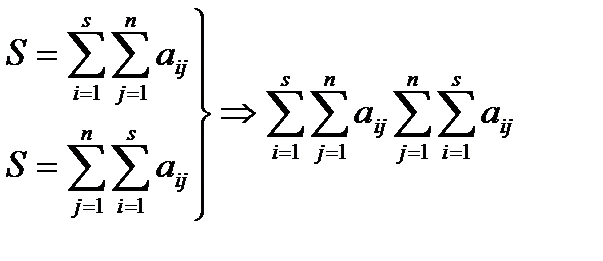
 - є лінійною комбінацією векторів системи (2)
- є лінійною комбінацією векторів системи (2)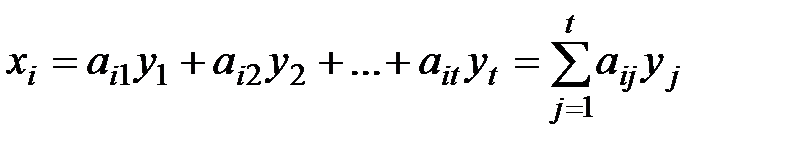 (i=1,2,…,S) (4)
(i=1,2,…,S) (4)



 -ку чисел, тобто матриця - це система п-векторів
-ку чисел, тобто матриця - це система п-векторів  -вимірного арифметичного простору.
-вимірного арифметичного простору. дорівнює р.
дорівнює р. , що виконується рівність:
, що виконується рівність:


 компонента -
компонента - 
 - лінійно залежний, а звідси випливає що
- лінійно залежний, а звідси випливає що  .
.
 . В цьому випадку
. В цьому випадку 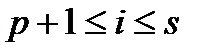 . В цьому випадку
. В цьому випадку  стає мінором р + 1 порядку матриці А, а тоді за умовою, він дорівнює нулю.
стає мінором р + 1 порядку матриці А, а тоді за умовою, він дорівнює нулю. .
. ,
, .
.

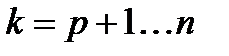 , то ми довели, що всі стовпці, починаючи з р + 1 є лінійними комбінаціями перших р- стовпців.
, то ми довели, що всі стовпці, починаючи з р + 1 є лінійними комбінаціями перших р- стовпців.



 випливає (з теореми про ранг), що в матриці А є мінор р - того порядку, не рівний нулю,
випливає (з теореми про ранг), що в матриці А є мінор р - того порядку, не рівний нулю,  , а всі мінори більш високих порядків дорівнюють нулю.
, а всі мінори більш високих порядків дорівнюють нулю. . Треба довести, що його рядки (стовпці) лінійно-залежні
. Треба довести, що його рядки (стовпці) лінійно-залежні
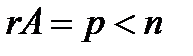
 , тоді з теореми про ранг випливає, що в А існує мінор d п - того порядку, не рівний нулю.
, тоді з теореми про ранг випливає, що в А існує мінор d п - того порядку, не рівний нулю.
 .
.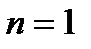 Тоді
Тоді  -і його рядки лінійно-залежні
-і його рядки лінійно-залежні 
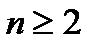 Тоді лінійна залежність рядків означає, що існує рядок, який є лінійною комбінацією інших.
Тоді лінійна залежність рядків означає, що існує рядок, який є лінійною комбінацією інших.


