
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мінори і алгебраїчні доповнення визначникаСодержание книги
Поиск на нашем сайте
Нехай задано визначник
Означення 1. Мінором Означення 2. Доповняльниммінороммінора Означення 3. Алгебраїчнимдоповненняммінора Лема до теореми Лапласа. Теорема Лапласа. Лема (про добуток мінору на його алгебраїчне доповнення). Добуток мінору М на його алгебраїчне доповнення А складається з деяких членів визначника d, причому ці члени входять в М∙А і в d з одними і тими ж знаками. Доведення. 1) Окремий випадок. Мінор М розташований в перших k рядках і в перших k стовпцях визначника d.
З'ясуємо, як пов'язані алгебраїчні доповнення і доповняльний мінор. A=M'(-1)1+2+…+k+1+2+..+k = M'(-1)2(1+2+..+k)=M' Розглянемо добуток М на А. М - алгебраїчна сума k! доданків. (1) а1α1.а2α2….аnαn - загальний член, де α1,α2,…,αk - перестановка з 1,2,…,k елементів Причому цей член (1) входить в М із знаком, який визначається парністю перестановки
Нехай α1,α2,…,αk має і1 інверсію, тоді загальний член М (-1)i1а1α1.а2α2….аkαk Загальний член А=М аk+1αk+1.аk+2αk+2….аnαn (2) αk+1,αk+2,…,αn - перестановки з k+1,k+2,…,n З'ясуємо, з яким знаком (2) входить до М:
Нехай αk+1,αk+2,…,αn має і2 інверсій, тоді загальний член М' буде (-1)i2аk+1αk+1.аk+2αk+2….аnαn Тоді загальний член М∙А буде набувати вигляду(3):
(-1)i1а1α1.а2α2….аkαk∙ (-1)i2аk+1αk+1.аk+2αk+2….аnαn= =(-1)i1+i2а1α1.а2α2….аkαk∙аk+1αk+1.аk+2αk+2….аnαn
Якщо розглянути (3) без знака, то бачимо що це буде якийсь член визначника n-го порядку d, тому що з кожного рядка і стовпця взято по одному елементу. З'ясуємо, з яким знаком цей член входить до визначника d. Для цього треба скласти підстановку з перших і других індексів
Розіб'ємо нижню перестановку на 2 частини. В І частині і1 інверсія за припущенням, в ІІ - і2 інверсія за припущенням. Жодний символ ІІ частини не утворює інверсій з символам І частини, тому що найменший символ ІІ частини k+1, найбільший символ І частини - k. Тому загальна кількість інверсій в нижній перестановці і1+і2.Таким чином, ми довели, що член (3) входить до М∙А і до визначника d з одним і тим же знаком (-1)i1+i2 Окремий випадок доведено. 2) Загальний випадок. Нехай мінор М знаходиться в рядках з номерами m1<m2<…<mk і стовпцями з номерами j1<j2<…<jk За допомогою перестановки рядків і стовпців заженемо вільно розташований мінор в лівий верхній кут. Ми хочемо, щоб m1 рядок був на 1-му місці, m2 - на 2-му, mk - на k-му. Тобто над рядком m1 зробимо m1-1 транспозицію, над рядком m2 - m2-2 транспозицію, над рядком mk - mk-1 транспозицію. Над j1стовпцем зробимо j1-1 транспозицію, над j2стовпцем зробимо j2-2 транспозицію, над jkстовпцем зробимо jk-1 транспозицію. Підрахуємо, скільки взагалі зроблено транспозицій: S=(m1-1)+(m2-2)+…+(mk-k)+(j1-1)+(j2-2)+…+(jk-k)= =m1+m2+…+mk+j1+j2+…+jk-2(1+2+…+k) Таким чином, ми змінили при цих перетвореннях знак визначника S раз. Одержали d1 Між цими визначниками існує співвідношення: d=(-1)Sd1=(-1)Sm-2(1+2+..+k)d1=(-1)Smd1(4) Для визначника d1 в І випадку було доведено, що М∙М' є d1. Якщо всі ці члени ми помножимо на (-1)Sm тоді (-1)Sm М∙М' є d1(-1)Sm, тобто M∙A є d. Теорема Лапласа. Якщо в визначнику d виділити k рядків, то визначник d дорівнює сумі добутків всіляких мінорів k-го порядку, розташованих в цих k рядках, на їх алгебраїчні доповнення. Доведення. Нехай задано визначник d.
Для визначеності проведемо доведення, виділивши перші k рядків. Складемо всілякі мінори k-го порядку, що знаходяться у перших k рядках. Нехай це будуть мінори М1,М2,…,Мs. Побудуємо до кожного з мінорів його алгебраїчне доповнення. Треба довести, що d = M1A1+M2A2+…+MsAs. Для доведення рівності доведемо 2 факти: кожний член d належить правій частині, і навпаки, кожний член правої частини є членом лівої частини. Другий факт безпосередньо випливає з леми про добуток мінору на його алгебраїчне доповнення. Доведемо перше. Візьмемо загальний член визначника d. а1α1.а2α2…аkαk∙аk+1αk+1.аk+2αk+2…аnαn, де α1,α2,…,αn - перестановка з 1,2,…,n Розіб'ємо загальний член на дві частини Для того, щоб збігались знаки розглянутого члена в d з М∙М', треба
Наслідок. Визначник дорівнює сумі добутків елементів будь-якого рядка на їх алгебраїчні доповнення.
Нехай в теоремі Лапласа k=1. Виділимо і-ий рядок. Тоді мінорами І порядку, розташованими в цьому рядку, будуть елементи цього рядка. З цього наслідку випливає, що обчислення визначника n-го порядку зводиться до обчислення n визначників (n-1)-го порядку. Користуючись властивістю 8) визначників можна звести обчислення визначника n-го порядку до обчислення лише одного визначника (n-1)-го порядку. Для цього доведемо, що в будь-якому рядку (якщо не всі елементи рядка нулі) за допомогою властивості 8) можна отримати всі нулі, крім одного. Нехай
Таким чином, обчислення визначника n-го порядку зведено попереднім перетворенням до обчислення визначника (n-1)-го порядку
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 643; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.58.141 (0.006 с.) |

 -го порядку
-го порядку  .
.
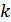 -го порядкувизначника
-го порядкувизначника  називається визначник порядку
називається визначник порядку 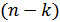 , отриманий з визначника
, отриманий з визначника  , взятий зі знаком
, взятий зі знаком 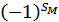 , де
, де  – сума номерів рядків і стовбців, у яких знаходиться
– сума номерів рядків і стовбців, у яких знаходиться 

 :
:
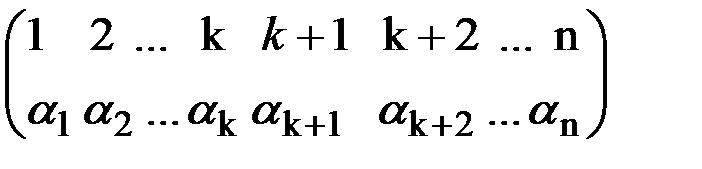

 . Таким чином, ми довели, що а1α1.а2α2…аkαk∙аk+1αk+1.аk+2αk+2…аnαn
. Таким чином, ми довели, що а1α1.а2α2…аkαk∙аk+1αk+1.аk+2αk+2…аnαn 
 замінити А1 (це випливає з леми). Таким чином, перший факт також доведений.
замінити А1 (це випливає з леми). Таким чином, перший факт також доведений.
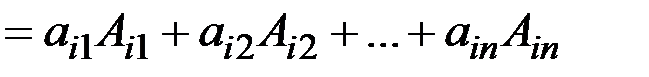
 . Зробимо такі перетворення. До другого стовпця додамо перший, помножений на
. Зробимо такі перетворення. До другого стовпця додамо перший, помножений на 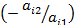 , …, до n-стовпця – перший помножений на
, …, до n-стовпця – перший помножений на  . Тоді отримаємо
. Тоді отримаємо





