
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття вектора, лінійні операції над векторами.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Векторна алгебра
Одним з важливих розділів даного курсу є загальна теорія лінійних алгебраїчних рівнянь. Ця теорія ґрунтується на понятті рангу системи векторів, арифметичному просторі. Тому попередньо слід вивчити векторний простір і пов’язані з ним поняття лінійної залежності, базису. Поняття абстрактного векторного простору є природним узагальненням геометричного простору, який в деякому ступеню вивчався в середній школі під назвою площина і простір. Але в шкільному курсі формально-алгебраїчний підхід до "вектора" ґрунтувався на прямокутних координатах точок (кінця і початку) вектора, (тобто первинним було поняття координат точки). В даному курсі розглядається інша концепція, яка приводить до узагальнення поняття площини, простору, до n-вимірного векторного простору. При розгляданні "Векторної алгебри" на площині і в просторі, доведеться розв’язувати систему лінійних алгебраїчних рівнянь, тому ми почнемо з методу Гаусса, розв’язування таких систем. Цей метод не потребує попередніх знань.
1.1 Системи лінійних алгебраїчних рівнянь. Метод послідовного виключення невідомих (метод Гаусса).
Запишемо загальну систему лінійних алгебраїчних рівнянь. Домовимось позначати коефіцієнти при невідомих Тоді систему

Означення 1. Розв’язком системи (1) називається упорядкована система n чисел, після підстановки яких замість Означення 2. Система (1) називається сумісною, якщо вона має принаймні один розв’язок. Якщо ж система не має жодного розв’язку, вона називається несумісною. Сумісні системи підрозділяються також на визначені і невизначені. Означення 3. Сумісна система називається визначеною, якщо вона має лише один розв’язок. В іншому разі сумісна система називається невизначеною. Основні задачі теорії лінійних рівнянь такі: 1. Дослідити систему на сумісність. 2. Сумісну систему дослідити на визначеність і невизначеність. 3. Дати алгоритми розв’язування.
Суть розв’язування систем рівнянь полягає в тому, щоб звести всі рівняння до рівнянь вигляду:
або до розв’язування одного рівняння з декількома невідомими з подальшим розв’язуванням рівнянь виду (2). Інструментом розв’язування системи є елементарні перетворення. Означення 4. Елементарними перетвореннями системи (1): 1) перестановка двох рівнянь; 2) множення обох частин деякого рівняння на число, не рівне 0; 3) додавання до одного з рівнянь іншого рівняння, в подумках помноженого на деяке число. Означення 5. Дві системи вигляду (1) з однаковою кількістю невідомих називаються еквівалентними, якщо вони або обидві несумісні, або, у разі сумісності, мають однакові розв’язки. Для самостійного доведення сформулюємо теорему: Теорема. Елементарні перетворення приводять до еквівалентних систем. Перейдемо до дослідження системи (1) лінійних алгебраїчних рівнянь методом Гаусса. Вважатимемо, що до до …………………………………………. до S рівняння + У результаті цих перетворень отримаємо еквівалентну систему

Зауваження. Могло трапитись, що у системі
У цьому випадку система Могло трапитись і таке:
Це рівняння можна задовольнити будь-яким набором чисел. Тому його можна викинути з системи. У системі до …………………………………………. до Тоді отримаємо таку еквівалентну систему:

Продовжуючи аналогічним чином, на останньому кроці отримаємо систему:

Формально треба дослідити три випадки: 1) У цьому випадку в останньому рівнянні невідомі
2) Система
Звідси
У цьому випадку на кожному кроці послідовно отримаємо рівняння вигляду (2). Математики кажуть, що систему зведено до трикутного вигляду. Система є визначеною. 1) Легко показати, що це неможливо. Припустимо супротивне
Ми отримали систему нееквівалентну початковій, що суперечить попередній теоремі. Отже, метод Гаусса вирішує основні задачі в теорії лінійних рівнянь: 1. Дослідження системи на сумісність. Система буде несумісною, якщо в процесі перетворень ми отримаємо рівняння, в якому коефіцієнти при всіх невідомих рівні нулю, а вільний член - відмінний від нуля. Якщо ж ми такого рівняння не зустрінемо, то система буде сумісною. 2. Сумісна система рівнянь буде визначеною, якщо вона зводиться до трикутного вигляду, і невизначеною, якщо зводиться до вигляду 3. Отримано алгоритм розв’язування системи алгебраїчних рівнянь методом послідовного виключення невідомих (метод Гаусса), поданий вище. Доведення. Нехай система векторів лінійно залежна за означенням 1.Треба довести, що вона лінійно залежна у сенсі означення 2. Скористаємось означенням 1. Тоді виконується (1):
Додамо до обох частин даної рівності вектор протилежний до
Внаслідок комутативності і означення нульового вектора маємо:
Тобто
Нехай тепер система векторів лінійно залежна за означенням 2:
Треба довести, що Додамо вектор
Відомо, що
Тобто система є лінійно залежною за означенням 1. Теорему доведено. Зауваження. При Теорема. Якщо у системі векторів є лінійно залежна підсистема, то і вся система лінійно залежна. Доведення. Нехай задана система Запишемо рівність в такому виді:
Тоді Система лінійно залежна за означенням 2. Теорему доведено. Означення. Система векторів З вище доведеної теореми випливає, що якщо система лінійно незалежна, то всі її підсистеми також лінійно незалежні. Доведення. Необхідність. Припустимо, що вектори Доведемо, що вектори колінеарні. Отже один з векторів є лінійною комбінацією. Нехай це Достатність. Припустимо, що Можливі випадки: 1) Принаймні один з векторів нульовий. Тоді твердження очевидне, тому що в системі міститься лінійно залежна підсистема. 2) Обидва вектори ненульові. Для доведення потрібна така лема. Лема. Якщо Дійсно, якщо Згідно із лемою маємо, що Теорему доведено. Теорема 3. Необхідною і достатньою умовою лінійної залежності трьох векторів є їх компланарність.
Доведення. Необхідність. Припустимо, що вектори Якщо серед векторів системи пара колінеарних, то очевидно, що вони є компланарними. Нехай тоді вектори попарно неколінеарні. Тоді за означенням 1 лінійної залежності існує вектор (наприклад, Візьмемо точку А і прикладемо до неї вектори
(для визначеності
Тоді з попередньої рівності випливає, що Достатність. Припустимо, що Якщо серед векторів системи пара колінеарних, то в системі є лінійно залежна підсистема і тому вся система залежна. Нехай тоді вектори попарно неколінеарні. Прикладемо вектори Оскільки Теорему доведено. Теорема 4. Довільні чотири вектори геометричного простору лінійно залежні. Доведення. Нехай маємо систему Візьмемо точку А і прикладемо до неї дані вектори. Побудуємо паралеліпіпед, діагональ якого є
За означенням додавання векторів маємо Тоді Теорему доведено. Зауваження. Мимохідь ми довели таке важливе твердження: будь-який вектор у просторі можна розкласти за трійкою некомпланарних векторів. Доведення. Доведемо цю теорему в просторі. Розглянемо базисні вектори Зауважимо, що можливість розкладання доведено у теоремі 4 про геометричний зміст лінійної залежності. Тож маємо Доведемо єдиність розкладання. Припустимо супротивне, що для
Зауважимо, що оскільки розкладання відрізняються, то різними є принаймні одна пара коефіцієнтів ci, di. Припустимо (для визначеності), що Тоді отримуємо:
Оскільки
Теорему доведено. Означення. Координатами вектора у заданому базисі називаються коефіцієнти розкладання цього вектора за векторами базису. Афінна система координат. Доведення. У афінній системі координат задані координати точки А, отже:
Отримали, що Теорему доведено. Прямокутна декартова система координат є окремим випадком афінної системи координат. При цьому базисні вектори взаємно перпендикулярні і мають одиничну довжину. Вони позначаються:
I. Скалярний добуток 1. Скалярна проекція вектора на вісь. Почнемо з допоміжного поняття величини напрямленого відрізку. Розглянемо вісь u і напрямлені відрізки на осі u. Означення 1. Величиною напрямленого відрізку
Розглянемо тепер вектори, що не обов’язково належать осі u.
Означення 2. Векторною проекцією вектора AB на вісь u називається вектор Позначимо векторну проекцію
Означення 3. Скалярною проекцією
Теорема 1. Скалярна проекція вектора на вісь дорівнює добутку довжини цього вектора на косинус кута між вектором та віссю. Доведення. (навести доведення) Для доведення властивостей скалярних проекцій векторів корисною є теорема про геометричний зміст декартових прямокутних координат. Теорема 2. Декартові прямокутні координати є проекціями вектора на відповідні координатні осі. Скалярна проекція має такі властивості. Теорема 3. Скалярна проекція суми двох векторів дорівнює сумі скалярних проекцій цих векторів
Доведення. (навести доведення) Теорема 4. Скалярна проекція добутку вектора на число дорівнює добутку цього числа на скалярну проекцію вектора
2. Поняття скалярного добутку. Означення 3. Скалярним добутком двох векторів
Останню рівність можна записати у вигляді
або
Звідси випливає інше означення скалярного добутку. Означення 4. Скалярним добутком векторів 3. Алгебраїчні та геометричні властивості скалярного добутку Доведемо, що скалярний добуток має такі алгебраїчні властивості: 1) 2) 3) 4) (навести доведення перелічених властивостей). Зауваження. З властивостей 3) та 1) випливає, що Зі скалярним добутком пов’язана така геометрична властивість: Для того щоб вектори були ортогональними (перпендикулярними) необхідно і достатньо, щоб їх скалярний добуток дорівнював нулю (навести доведення необхідності і достатності умови).
4. Вираз скалярного добутку через координати векторів Означення. Базис простору (площини) називається ортонормованим, якщо він складається з попарно ортогональних векторів, довжина яких дорівнює одиниці.
Нехай в просторі введено ортонормований базис
Теорема. Скалярний добуток
II. Векторний добуток 1. Поняття векторного добутку Введемо спочатку поняття 1)правої та 2)лівої трійки векторів. Означення 1. Упорядкована трійка векторів a, b, c називається правою, якщо з кінця останнього вектора поворот від першого до другого спостерігається проти годинникової стрілки, якщо ж за годинниковою, то трійка векторів називається лівою. Тепер можна ввести поняття векторного добутку. Означення 2. Векторним добутком векторів 1) 2) вектор 3) трійка векторів
2. Геометричні та алгебраїчні властивості векторного добутку. Геометричні властивості пов’язані з векторним добутком містять дві наступні теореми. Теорема 1. (про геометричний зміст довжини векторного добутку). Довжина векторного добутку дорівнює добутку довжин цих векторів на синус кута між ними. Доведення. (навести доведення). Теорема 2. Для того щоб два вектори були колінеарними необхідно і достатньо, щоб їх векторний добуток дорівнював нульовому вектору. Доведення. (навести доведення). Розглянемо алгебраїчні властивості векторного добутку: 1) 2) 3) 4) Доведення. (навести доведення). Рекомендації щодо доведення дистрибутивності векторного добутку. Крім доведення, поданого в основному підручнику [1] (література, навчально-методична), можна запропонувати більш геометричне доведення [9]. Наведемо його. Отже треба довести, що Ця рівність очевидна, коли принаймні один з векторів нульовий. Нехай тепер усі вектори ненульові. Проведемо спочатку доведення, в окремому випадку, коли
 . .
Спроектуємо точку А на площину, отримаємо вектор
Доведемо, що ці вектори однаково напрямлені. Вектор Перейдемо до доведення рівності Прикладемо до точки О вектори
За означенням додавання векторів маємо
Доведемо дистрибутивність в загальному випадку. Для цього подамо
що і треба було довести.
3. Вираз координат векторного добутку через координати векторів. Нехай вектори Треба знайти координати вектора Для того щоб це зробити, треба попередньо скласти таблицю множення
Доведення таблиці множення (навести доведення). Використовуючи таблицю множення, доведемо, що розкладання вектора
Доведення (навести доведення).
III. Мішаний добуток. 1. Поняття мішаного добутку Означення 1. Мішаним добутком трьох векторів
2. Геометричні та алгебраїчні властивості. Теорема 1 (про геометричний зміст мішаного добутку). Мішаний добуток векторів
Доведення (навести доведення). З цієї теореми можна отримати наслідок. Наслідок. Для того щоб три вектори Наслідком теореми 1 є також така алгебраїчна властивість
(Навести доведення цієї властивості). Оскільки з доведеної рівності виходить, що квадратні дужки можна поставити будь-як, то домовились позначати мішаний добуток так Що стосується інших алгебраїчних властивостей, то є наслідками скалярного і векторного добутку. Наприклад, можна довести, що (Навести доведення)
3. Вираз мішаного добутку через координати векторів. Нехай в ортонормованому базисі
Треба знайти вираз Користуючись властивостями скалярного і мішаного добутків, можна довести таку формулу:
Поняття лінійного прос |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.23.103 (0.016 с.) |

 . Перший індекс вказує номер рівняння, другий індекс – номер невідомого. Невідомі (змінні) позначатимемо буквами
. Перший індекс вказує номер рівняння, другий індекс – номер невідомого. Невідомі (змінні) позначатимемо буквами  , а вільні члени –
, а вільні члени –  .
. рівнянь з
рівнянь з  невідомими можна записати у вигляді:
невідомими можна записати у вигляді: відповідно, кожне рівняння перетворюється на правильну числову рівність.
відповідно, кожне рівняння перетворюється на правильну числову рівність.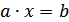 (2)
(2) . Якщо це не так, цього можна досягти за рахунок або перестановки рівнянь, або за рахунок перенумерації невідомих. Зробимо такі елементарні перетворення над системою (1):
. Якщо це не так, цього можна досягти за рахунок або перестановки рівнянь, або за рахунок перенумерації невідомих. Зробимо такі елементарні перетворення над системою (1): рівняння +
рівняння +  -ше рівняння
-ше рівняння 
 рівняння +
рівняння + 


 (3)
(3) , несумісна.
, несумісна. (4)
(4) . Цього можна досягти за рахунок або перестановки рівнянь, або за рахунок перенумерації невідомих. Зробимо такі елементарні перетворення над системою
. Цього можна досягти за рахунок або перестановки рівнянь, або за рахунок перенумерації невідомих. Зробимо такі елементарні перетворення над системою 
 -го рівняння +
-го рівняння + 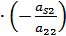


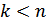
 оголосимо вільними у тому сенсі, що їм можна надавати будь-які значення. Тоді з останнього рівняння знайдемо
оголосимо вільними у тому сенсі, що їм можна надавати будь-які значення. Тоді з останнього рівняння знайдемо 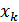 , отже передостаннє рівняння і всі інші послідовно стають рівняннями виду (2)
, отже передостаннє рівняння і всі інші послідовно стають рівняннями виду (2) 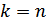
 набуває вигляду:
набуває вигляду:


 . Тоді останнє рівняння стає таким:
. Тоді останнє рівняння стає таким:
 .
. :
:

 , що виконується і рівність
, що виконується і рівність  і система лінійно залежна за означенням 2.
і система лінійно залежна за означенням 2. (
( ).
). .
. до лівої та правої частини даної рівності:
до лівої та правої частини даної рівності:
 маємо:
маємо:
 , означення 1 лінійної залежності втрачає сенс, тоді як за означенням 2 рівність
, означення 1 лінійної залежності втрачає сенс, тоді як за означенням 2 рівність  , тобто
, тобто 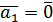 . Маємо, що система з одного вектора лінійно залежна тоді і тільки тоді, коли цей вектор нульовий.
. Маємо, що система з одного вектора лінійно залежна тоді і тільки тоді, коли цей вектор нульовий. . Візьмемо її підсистему. Не зменшуючи загальності міркувань вважатимемо, що підсистема
. Візьмемо її підсистему. Не зменшуючи загальності міркувань вважатимемо, що підсистема  – лінійно залежна. Тоді
– лінійно залежна. Тоді  :
:  .
.
 такі, що
такі, що  .
. .
. утворюють лінійно залежну систему.
утворюють лінійно залежну систему. (для визначеності). Тоді
(для визначеності). Тоді  , тобто вектори колінеарні.
, тобто вектори колінеарні. . Покажемо, що система лінійно залежна.
. Покажемо, що система лінійно залежна. , то
, то  :
:  , то
, то 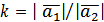 , якщо
, якщо  , то
, то  .
. утворюють лінійно залежну систему. Покажемо, що вони компланарні.
утворюють лінійно залежну систему. Покажемо, що вони компланарні. ), що є лінійною комбінацією інших
), що є лінійною комбінацією інших  .
. .
.


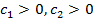 )
) – сторони і діагональ паралелограма. Отже ці вектори компланарні. Оскільки
– сторони і діагональ паралелограма. Отже ці вектори компланарні. Оскільки  , то вектори
, то вектори  також компланарні.
також компланарні. . Тоді
. Тоді  .
. , то
, то  . Тоді
. Тоді  , тобто
, тобто  . Якщо серед них є трійка компланарних, то вони очевидно лінійно залежні. Нехай такої трійки немає.
. Якщо серед них є трійка компланарних, то вони очевидно лінійно залежні. Нехай такої трійки немає.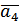 , а ребра знаходяться на прямих, що містять вектори
, а ребра знаходяться на прямих, що містять вектори 
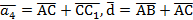 . Оскільки
. Оскільки  , маємо
, маємо  .
. , а тому
, а тому 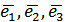 . Візьмемо довільний вектор
. Візьмемо довільний вектор  .
. .
. .
. .
.




 має координати
має координати  .
.
 називається число, що позначається
називається число, що позначається  :
:
 , де
, де  ортогональна проекція точки A,
ортогональна проекція точки A,  – отрогональна проекція точки B.
– отрогональна проекція точки B.
 вектора
вектора  .
. .
. .
. і
і  називається число
називається число  , що дорівнює добутку довжин цих векторів на косинус кута між ними.
, що дорівнює добутку довжин цих векторів на косинус кута між ними.



 (властивість симетрії)
(властивість симетрії) (дистрибутивність)
(дистрибутивність)

 .
.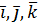 , тобто
, тобто 
 нехай далі вектори
нехай далі вектори  , відповідно.
, відповідно. в ортонормованому базисі дорівнює сумі добутків відповідних координат векторів
в ортонормованому базисі дорівнює сумі добутків відповідних координат векторів 
 і задовольняє умови:
і задовольняє умови: (
( є правою.
є правою. (антикомутативність);
(антикомутативність); ;
; (дистрибутивність);
(дистрибутивність); .
. . Для цього опишемо геометричну побудову вектора
. Для цього опишемо геометричну побудову вектора 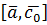 . До довільної точки O простору прикладемо вектори
. До довільної точки O простору прикладемо вектори  . Через точку O проведемо площину перпендикулярну
. Через точку O проведемо площину перпендикулярну  :
: 

 . Повернемо
. Повернемо  , отримаємо вектор
, отримаємо вектор  . Доведемо, що вектор
. Доведемо, що вектор 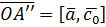 . Насправді ці вектори мають однакову довжину, тому що
. Насправді ці вектори мають однакову довжину, тому що ,
, .
. .
. ,
,  . За правилом трикутника побудуємо вектор
. За правилом трикутника побудуємо вектор  . Спроектувавши точки А і В, отримаємо вектори
. Спроектувавши точки А і В, отримаємо вектори  . Повернемо їх в площині на кут g w:val="UK"/></w:rPr><m:t>2</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
. Повернемо їх в площині на кут g w:val="UK"/></w:rPr><m:t>2</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  .
. . Але з наведеної вище конструкції випливає, що
. Але з наведеної вище конструкції випливає, що 
 . А тому з попередньої рівності випливає:
. А тому з попередньої рівності випливає: , де
, де  . Тоді можна записати
. Тоді можна записати ,
, .
.



 .
.
 були компланарними необхідно і достатньо, щоб їх мішаний добуток дорівнював нулю.
були компланарними необхідно і достатньо, щоб їх мішаний добуток дорівнював нулю.
 .
.
 .
.



